Контрольное задание № 7
по теме «Дифференциальное исчисление функций нескольких переменных»
(10 вариантов)
Дана функция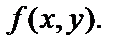 
1. Исследовать функцию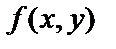 
на экстремум. Найти экстремальные значения функции.
2. Найти наибольшее и наименьшее значения функции 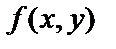в заданной области D.
3. Составить уравнение касательной плоскости к поверхности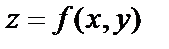 
в точке, где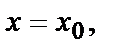 
4. Найти величину наибольшей скорости возрастания функции 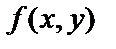в точке М1(х1,у1).
5. Вычислить производную функции 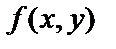в точке М1(х1,у1) в направлении вектора 
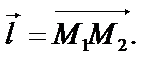Каков характер изменения функции? Почему?
6. Найти угол между градиентами функции 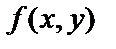в точках М1(х1,у1) и М2(х2,у2). Построить векторы и указать угол.
| № вар. | Функция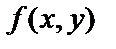
| Область D |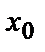 
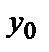
| М1(х1,у1) | М2(х2,у2) |
| Треугольник с вершинами О(0,0), А(-5,0), В(0,-5) | 
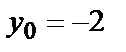
| М1(-1,0) | М2(0,1) М2(0,–1) | |
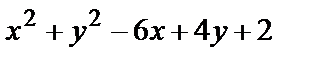
| Прямоугольник с вершинами А(1,-3), В(1,2), С(4,2), Е(4,-3) | 
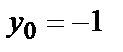
| М1(2,-3) | М2(1,-1) | |
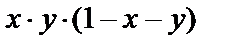
| Треугольник с вершинами А(2,0), В(0,2), С(0,-2) |
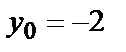
| М1(1,1) | М2(1,-1) | |
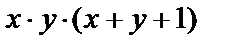
| Область D ограничена линиями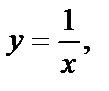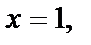    
| 
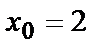
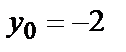
| М1(-2,1) | М2(2,0) | |
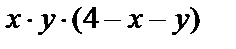
| Треугольник с вершинами А(1,0), В(6,0), С(1,5) | 
| М1(-1,2) | М2(-2,1) | |
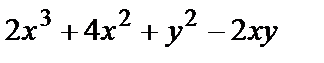
| Область D ограничена линиями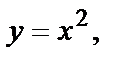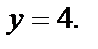  
| 
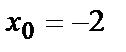
| М1(-2,0) | М2(-1,-2) | |
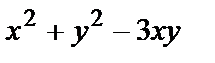
| Четырёхугольник с вершинами О(0,0), С(0,-2), А(2,0), В(2,2). |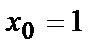 
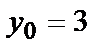
| М1(-1,1) | М2(2,2) | |
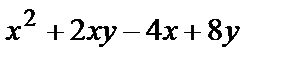
| Параллелограмм с вершинами О(0,0), А(-1,0), В(0,2), С(1,2) |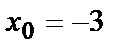 
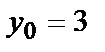
| М1(2,-1) | М2(-2,2) | |
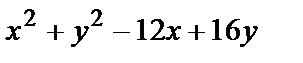
| Четырёхугольник с вершинами О(0,0), С(-1,1), А(0,1), В(1,0). |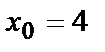 
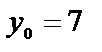
| М1(2,-5) | М2(4,-6) | |
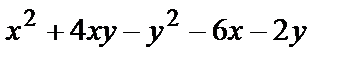
| Треугольник с вершинами О(0,0), А(3,0), В(0,2) |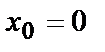 
| М1(2,0) | М2(2,1) |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Дата добавления: 2014-12-30; просмотров: 889;