Несобственные интегралы
При введении понятия определенного интеграла мы предполагали, что отрезок интегрирования является конечным. Если промежуток интегрирования бесконечен, то требуется специальное определение таких интегралов - они называются несобственными.
Определение. Пусть функция 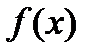 непрерывна на
непрерывна на 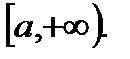 Тогда полагают:
Тогда полагают:
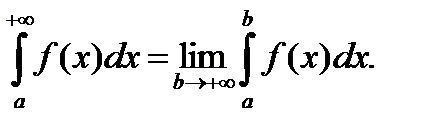
Если этот предел равен числу, то несобственный интеграл 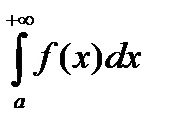 называется сходящимся. Если этот предел равен бесконечности или не существует, то - расходящимся.
называется сходящимся. Если этот предел равен бесконечности или не существует, то - расходящимся.
Пример 45.
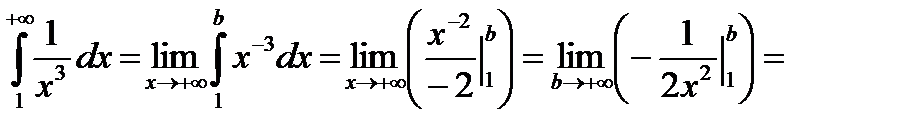
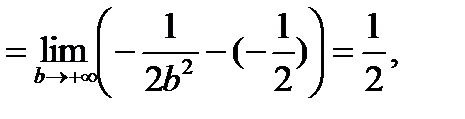 т.е. интеграл сходится.
т.е. интеграл сходится.
Пример 46.
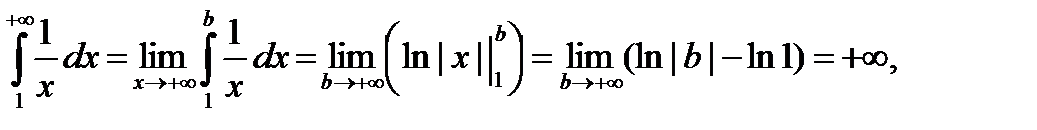
т.е. интеграл расходится.
Есть и другие варианты несобственных интегралов с бесконечными пределами интегрирования - они определяются аналогично:
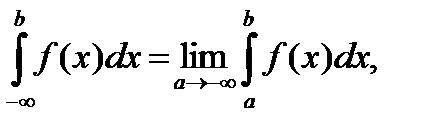
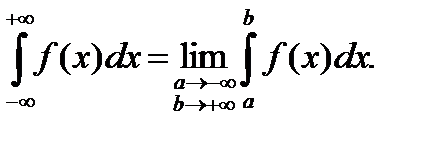
Пример 47.
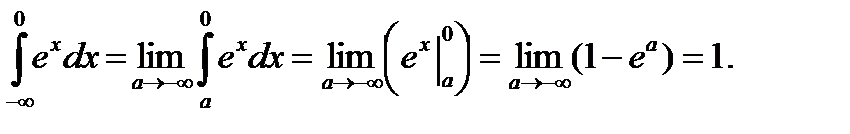
Пример 48.
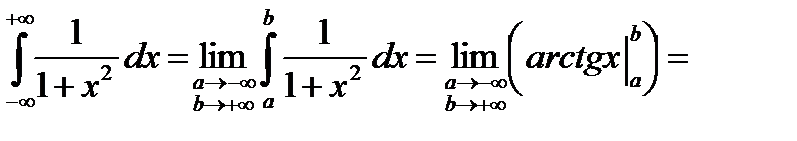
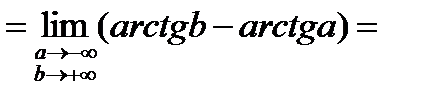 (см. график
(см. график 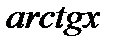 в части 3,
в части 3,
стр. 7) = 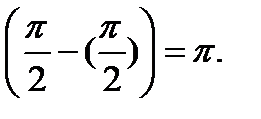
Замечание.Геометрический смысл интеграла сохраняется и для несобственных интегралов - это «площадь» криволинейной трапеции, «уходящей в бесконечность», ограниченной графиком подынтегральной функции и промежутком интегрирования.
4.12. Примеры выполнения контрольных заданий по теме «Интегральное исчисление»
Задание 1. Вычислить неопределенные интегралы.
а) 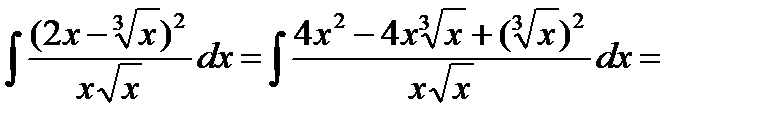
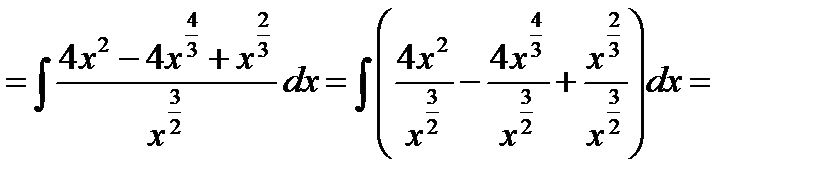
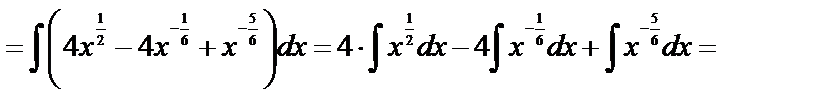
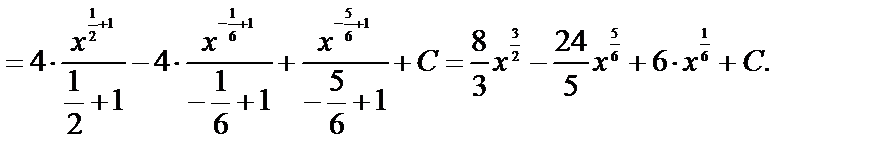
б) Метод замены переменной.
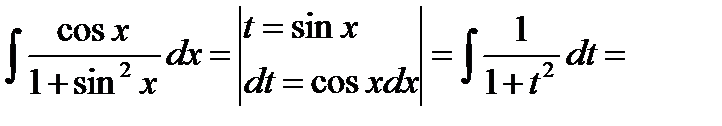 (табличный интеграл) =
(табличный интеграл) = 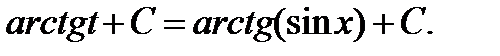
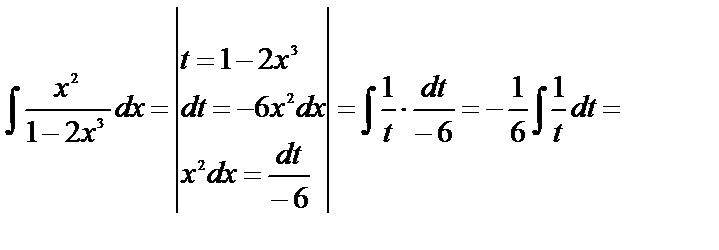
= (табличный интеграл) = 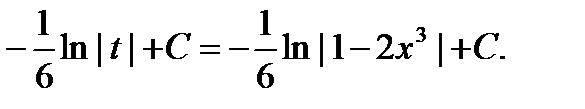
в) Метод интегрирования по частям.
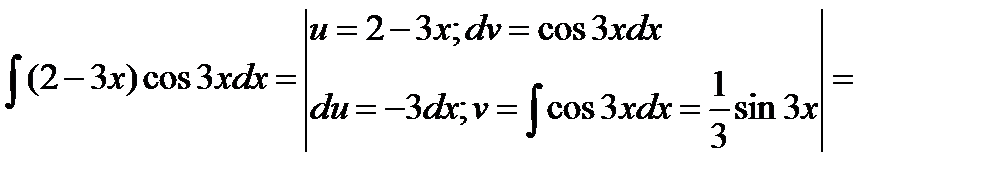
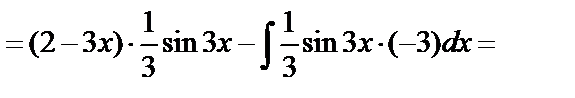
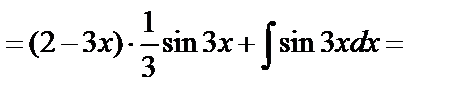
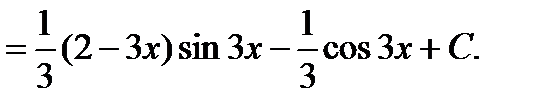
г) Интегралы специального вида (см. п. 4.5, интеграл вида 1).
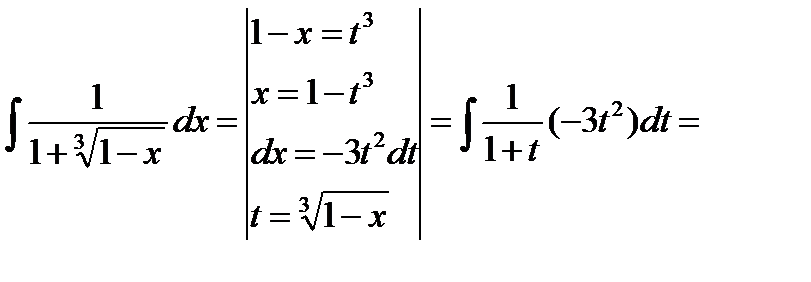
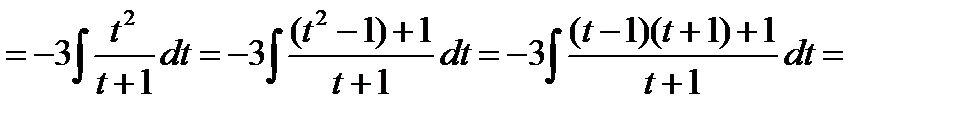
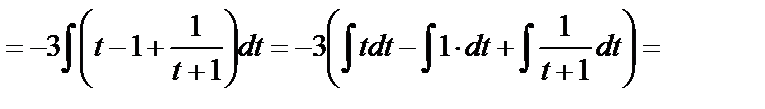
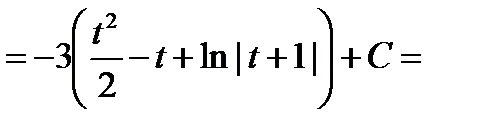
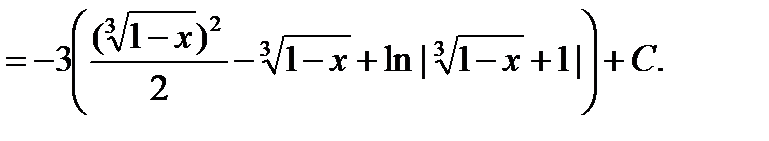
д) Интегралы специального вида (см. п. 4.5, интеграл вида 2).
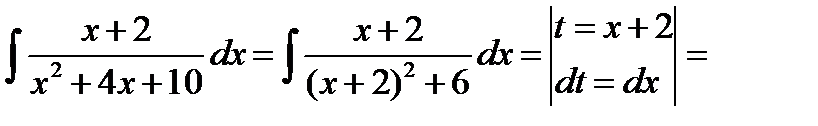
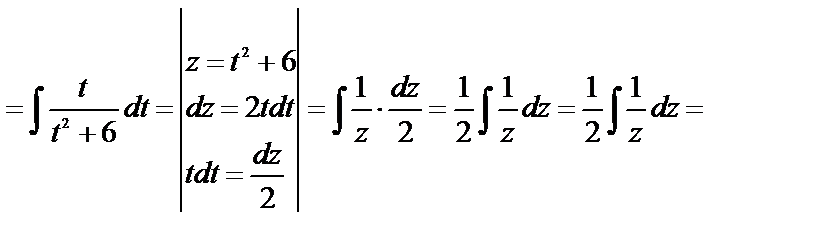
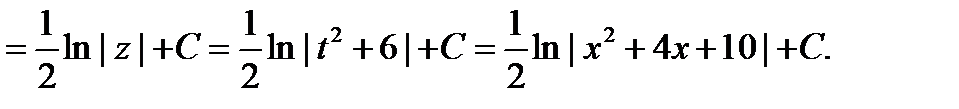
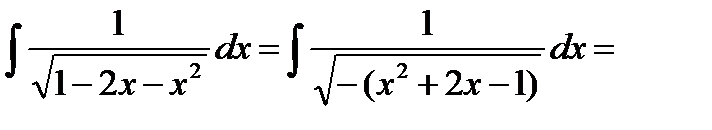
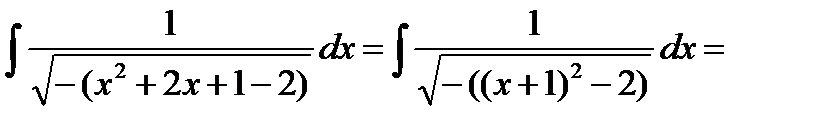
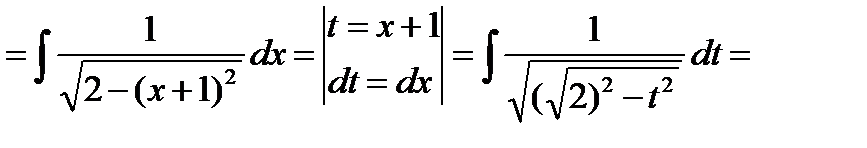
= (табличный интеграл) = 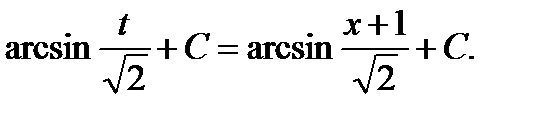
Дата добавления: 2014-12-30; просмотров: 1038;
