Функции распределения

Согласно молекулярно-кинетической теории молекулыидеального газа находятся в непрерывном хаотическом движении с равномерным распределением по направлениям.

Скорости молекул при этом изменяются по величине. Наиболее близкой к истинному значению скорости является средняя квадратичная скорость молекул, которая для газа массой "m" находящегося в состоянии равновесия при T=const остаётся постоянной:

Статистический закон Максвелла указывает на существование некоторой наиболее вероятной скорости движения молекул, в окрестности которой в интервале v, v+dv находится большее число молекул, чем в окрестности другой скорости.

Максвелловский закон распределениямолекулидеального газапо скоростям в стационарном состоянии выражается формулой:

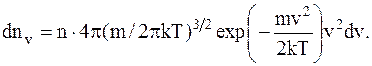
где dn_v – среднее число молекул в единице объема со скоростями в интервале от v до v+dv;

n – число молекул в единице объема.

Откуда

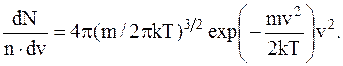
где dN/ndv – функция распределения, которая показывает, какая доля молекул от их общего числа отнесена к некоторому интервалу скоростей.

Для наиболее вероятной скорости движения молекул была получена формула:

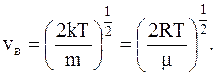
Кроме <v_кв> и v_в для описания движения молекул идеального газа вводится понятие средней арифметической скорости:

Для расчета числа молекул, движущихся со скоростями в интервале от v до v+dv, часто вводят понятие относительной скорости u=v/v_в, тогда закон распределения Максвелла имеет вид:

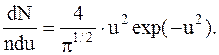
Атмосферное давление на какой-либовысоте обусловлено весом вышележащих слоев газа.

Если давление газа на высоте h_o-p_o, а высоте h-p, то

p=p_o exp(-mgh/kT).

Данное соотношениеназывают барометрической формулой, которая показывает, чтодавление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже его температура.

Заменив в барометрической формуле значениядавлений, на число молекул в единице объема получим

n=n_o exp(-mgh/kT).

но R=m/k, тогда

n=n_o exp(-mgh/RT).

Полученнаяформулаопределяет закон распределения молекул газа по высоте в поле сил тяготения.

Но mgh=W_p – потенциальная энергия молекул в поле сил тяготения, следовательно:

n=n_o×exp(-Wp/kT),

где n_o – число молекул в единице объема в том месте, где потенциальная энергия молекул равна нулю;

n – число молекул в единице объема в тех точках пространства, где потенциальная энергия молекул равна Wp.

Это распределение и называют распределением Больцмана, которое дает распределениечастиц по значениям потенциальной энергии.

Плотность газа в зависимости от высоты изменяется по закону:

r=r_o×exp(-m_ogh/кТ),

где m_o – масса одной молекулы.

Прямолинейные участки траектории, проходимые молекулой между двумя последовательнымисоударениями, называются свободными пробегами.

Средняя длина свободного пробега

,

,

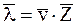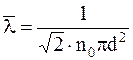где n_o – число молекул в единице объёма.

Среднее число соударений <Z>, численно равно отношению средней скорости движения молекул <v> и <l>:

;

,

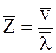где s – эффективное сечение.

Минимальное расстояние, на которое сближаются при столкновении центры 2-х молекул, называется эффективным сечением.

Используя основное уравнение кинетической теории газов p=n_okT,

можно записать

.

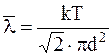Средняя длина свободного пробега при какой-то температуре Т может быть определена по формуле:

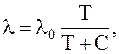
где C – постоянная Сезерленда, зависящая от интенсивности молекулярных взаимодействий;

l_o – длина свободного пробега молекул без учёта их взаимодействий.