Данное уравнение является общей формой записи закона распределения скоростей молекул, справедливой для любых интервалов скоростей.

Учитывая, что относительная скорость u=v/v_в и что в нашей задаче v₁=v_в и v₂=4, получим: u₁=1, и u₂=¥. Следовательно, искомая часть молекул:

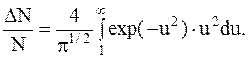
Чтобы избежать математических трудностей, связанных с нахождением неопределенного интеграла, воспользуемсятем очевидным фактом, что скорости всех молекул лежат в интервале от 0 до ¥. Поэтому, если обозначить через DN' число молекул, скорости которых меньше наиболее вероятной, т.е. лежат в интервале от 0 до 1, то можно записать:

.

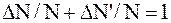Таким образом, вместо того, чтобы искать DN/N можно найти

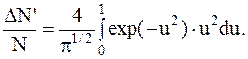
а затем вычислить DN/N.

Так как зтот интеграл аналитически не вычисляется, воспользуемся методом приближенного интегрирования. Для этого разложим подынтегральную функцию f(u)=exp(-u²)×u² в ряд Маклорена:

exp(-u²)=1-u²/1+u⁴/2–u⁶/6+u⁸/24-...

exp(-u²)× u²=u²- u⁴/1+u⁶/2–u⁸/6+u¹⁰/24-...

Теперь, произведя интегрирование, имеем:

DN'/N=4(1/3-1/5+1/14-1/54+1/264...)/p^1/2.

Ограничиваясь первыми четырьмя членами разложения, найдем с погрешностью, не превышающей 0,01:

DN'/N=0,43.

Тогда

DN/N=1-0,43=0,57.

1.3.9. Найти число столкновений <Z>, которые происходят в течение секунды между всеми молекулами, находящимися в объеме V==1,0 мм³ водорода при нормальных условиях. Принять для водорода d=2,3×10^-10 м.

Решение. Число столкновений <z>, испытываемых одной молекулой за одну секунду, определяется по формуле

<z>=2 ^1/2pd²×n²×<v>×V/2,

где d – эффективный диаметр молекулы;

n – концентрация молекул;

<v>=(8RT/pm)^1/2 – средняя арифметическая скорость молекул газа.

Чтобы установить соотношение между величинами <z> и <Z>, учтем, что если умножить число столкновений одной молекулы за одну секунду на число всех молекул N, то получим результат, превышающий в два раза искомое число <Z>. Действительно, в одном столкновении участвуют сразу две молекулы, поэтому в число <z>×N каждое столкновение входит дважды: один раз в счет столкновений одной из молекул данной пары, другой раз в счет столкновений второй молекулы. Следовательно, правильным будет выражение

<Z>=<z>N/2=<z>nV/2,

где n =p/kT – концентрация молекул.

Подставив вместо <z>, n и <v> их значение, окончательно получим:

<Z>=2 ^1/2pd²p²V(8R/pmT)^1/2/2k²T.

Выразим входящие в формулу величины в единицах СИ, подставив их в формулу и выполнив вычисление, будем иметь

<Z>=1,6×10²⁶ с^-1.

1.3.10. Пылинки массой m=10^-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура T воздуха во всем объеме одинакова и равна 300 К.

Решение. При равновесном распределении пылинок концентрация их зависит только от координатыz по оси, направленной вертикально. В этом случае к распределению пылинок можноприменить формулу Больцмана

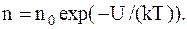
Так как в однородном поле силы тяжести U=mgz, то

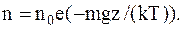
По условию задачи, изменение Dn концентрации с высотой мало по сравнению с n (Dn/n=0,01), поэтому без существенной погрешности изменение концентрации n можно заменить дифференциалом dn.

Дифференцируя выражение по z, получим

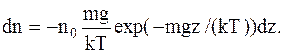
Так как

n_oexp(-mgz/(kT))=n,

то

dn=- mgndz/kT.

Отсюда находим интересующее нас изменение координаты:

dz=-kT dn/mgn.

Знак минус показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0).

Знак минус опустим (в данном случае оннесущественен)и заменим дифференциалы dz и dn конечными приращениями Dz и Dn:

Dz=kTDn/mgn.

Выразив входящие вформулувеличины в системе СИ, подставив их в эту формулу, произведем вычисления

Dz=1,38×10^-23×300×0,01/10^-21×9,81=4,23×10^-3 м=4,23 мм.

1.3.11. Барометр в кабине летящего самолета все время показывает одинаковое давление p=79 кПа, благодаря чему летчик считает высоту h полета неизменной. Однако температура воздуха за бортом самолета изменилась с t=5^oC до t=1 ^oC. Какую ошибку h в определении высоты допустил летчик? Давление p у поверхности Земли считать нормальным.

Решение. Для решения задачи воспользуемся барометрической формулой

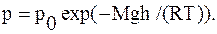
Барометр может показывать неизменное давление p при различных температурах T₁и T₂ за бортом только втом случае, если самолет находится не навысоте h₁ (которую летчик считает неизменной), а на некоторой другой высоте h ₂.

Запишем барометрическую формулу для двух случаев:

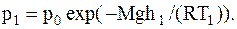
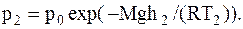
Найдем отношение p_o/p и обе части полученных равенств, прологарифмируем:

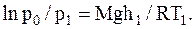
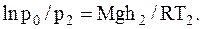
Из полученных соотношений выразим высоты h₁ и h₁ и найдем их разность

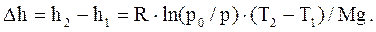
Проверим, дает ли правая часть полученногоравенства единицу длины:

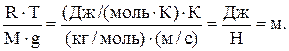
Выразив величины в СИ, подставив их в полученную формулу, произведем вычисления:

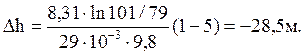
1.3.12. Средняя длина свободного пробега <l> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость <v> молекул и число <z> соударений, которые испытывает молекула в 1с.

Решение. Средняя арифметическая скорость молекул определяется по формуле

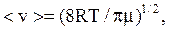
где m – молярная масса вещества.

Среднее число <z> соударений молекулы в 1 с определяется отношением средней скорости <v> молекулы к средней длине ее свободного пробега <l>:

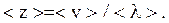
Размерность полученных величин очевидна. Подставив значения входящих в формулы величин в СИ, будем иметь

<v>=362 м/с;

<z>=9,05×10⁹ с^-1.