После сокращений на a/27b и в правой части на R получи

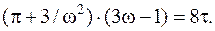
Это и есть уравнение Ван-дер-Ваальса в приведенной форме. Ононе содержит никаких параметров, характеризующих индивидуальные свойства газа, и поэтому является универсальным.

Теперь ответим на вопрос задачи. Так какдавление остается постоянным (p=p_кр), то p=1; молярный объем газа согласно условию увеличился в два раза, т.е. V_m=2V_mкр; следовательно, w=2.

Из уравнения выразим приведенную температуру:

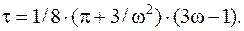
Подставив сюда значения и произведя вычисления, найдем t=35/32.

Температура T, как отмечалось, связана с приведенной температурой t и критической T_кр соотношением T=tT_кр. Произведя вычисление по этой формуле, получим

T=322 К.

1.4.3. В цилиндре под поршнем находится хлор массой m=20 г. Определить изменение DU внутренней энергии хлора при изотермическом расширении его от V₁=200 см³ до V₂=500 см³.

Решение. Внутренняя энергия U реального (вандерваальсового) газа определяется выражением

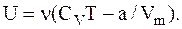
Выразив в этом выражении молярный объем V_m через объем V и количество вещества n ( V_m=V/n) и учтя, что n=m/m, получим

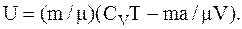
Изменение внутренней энергии в результате изотермического расширения найдемкак разность двух значений внутренней энергии при объемах V₂ и V₁:

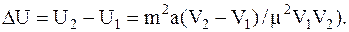
Подставив значения величин в СИ и произведя вычисление, получим:

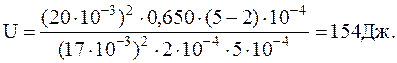
Заметим, что для идеального газа такое изменениевнутренней энергиисоответствовалобы нагреванию на 26,3 К.

1.4.4. В очень прочном стальном баллоне заключена вода, занимающая при комнатной температуре половину объема баллона. Найти давление (в технических атмосферах) и плотность водяных паров при повышении температуры до 400 ^oС.

Решение. Из таблицы критических температур возьмем для воды t=374 ^oС. Таким образом, при нагревании воды в баллоне до 400 ^oС она оказалась при температуре выше критической. Следовательно, она вся будет находится в газообразном, или, как это принято говорить в отношении воды, парообразном состоянии.

Плотность водяного пара определим,учитывая, что объем одной и той же массы воды в результате ее нагреванияувеличился в два раза (массу паров, находящихся над водой при комнатной температуре, можно не учитывать). Следовательно, плотность пара, равная отношению массы к объему, будет вдвое меньше плотности воды r_В=1×10³ кг/м³:

r=r_В/2=5×10² кг/м³.

Так как плотность пара в баллоне оказаласьбольшойпо сравнению с плотностями газов при нормальных условиях (например, плотность воздуха при нормальных условиях равна 1,29 кг/м³), то, очевидно, водяной пар здесь можно рассматривать как реальный газ, параметры которого связаны уравнением состояния Ван-дер-Ваальса:

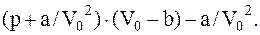
Решив его относительно p, получим

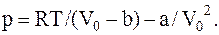
Здесь V_o – молярный объем, но не объем всей массы пара. Поэтому на основании определения плотности можно записать

V_o=m/r,

где m – молярная масса пара.

Подставив это значение V_o в вышенаписанную формулу, найдем

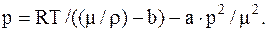
Взяв из таблиц значения постоянных a и b для воды, выразив все величины, входящие в формулу, в единицахСИ: Т=673 К, а =0,55 м⁴×Н/моль², b=3×10⁵ м³/моль, m=0,018 кг/моль. Выполнив вычисления, найдем

p=5,1×10⁸ Па=5,2×10³ ат.

1.4.5. Определить давление m=280 г азота, находящегося при температуре 27 ^oС в сосуде, объем которого равен: 1) V=1,00 м³; 2) V=0,50 л.

Решение. Чтобы решить вопрос о том, каким следует считать данный газ-идеальным или реальным,-найдем молярныйобъем газа V_o. Пусть в сосуде содержится n=m/m молей газа. Тогда

V_o=V/n=Vm/m.

Учитывая, что молярная масса азота m=0,028 кг/моль, получим:

1) Vo=1,00×0,28/0,28=0,10 м³/моль;

2) Vo=0,5×10^-3×0,028/0,28=5,0×10^-5 м³/моль.

Сравнивая вычисленные значения V_o с молярным объемом газа при нормальных условиях V_{o(норм) =}22,4×10^-3 м³/моль, видим, что в первом случае газ достаточно разряжен и его можно считать идеальным. Уравнение состояния идеального газа для одного моля запишем так:

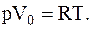
Отсюда

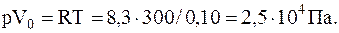
Во втором случае V_o<V_o(норм), и газ следует считать реальным. Его давление найдем из уравнения Ван дер Ваальса для реального газа

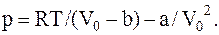
Взяв из таблиц значения постоянныхВан-дер-Ваальсадля азота: a=0,13 м⁴×Н/моль², b=3,7×10^-5 м³/моль, произведем вычисление, получим:

p=1,4×10⁸ Па.

Заметим, что, вычисляя давление по формуле, характерной для состояния идеального газа, получили бы в этом случае неверный результат: p=0,5×10⁸ Па.

1.4.6. Определить массу кислорода в баллоне объемом V=10,0 л при температуре 27 ^oС и давлениях:1)p₁=1,00 ат; 2)p₂=410 ат.

Решение. В первом случае (p=1,00 ат) кислород в баллоне находитсяпри условиях, близких кнормальным. То обстоятельство, что температура газа несколько вышенормальной, означает лишь, что его плотность при этом давлении меньше, чем при нормальных условиях. Поэтомубез большой погрешностиможно считать газ идеальным. На основании уравнения состояния идеального газа, учитывая, что для кислорода m=0,032 кг/моль, получим:

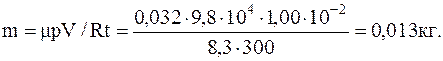
Во втором случае (p=410 ат), учитывая большое по сравнению с нормальным давление газа, следует считать его реальным и вести расчеты на основании уравнения Ван дер Ваальса.

Масса газа определяется соотношением:

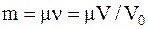
где m – молярная масса;

n – число молей;

V – объем газа;

V_o – его молярный объем.

Таким образом, необходимо из уравнения Ван-дер-Ваальса

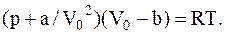
найти величину V_o, а затем массу газа.

Уравнение Ван дер Ваальса является уравнением третьей степени относительно Vo и поэтому имеет, вообще говоря, три корня. Однако, учитывая, что кислород в баллоне находится при температуре выше критической (t_кр=-119 ^oС), можно утверждать, что при определенном давлении газ будет иметь лишь один определенный объем. Следовательно, кубическое относительно V_o уравнение Ван-дер-Ваальса имеет в данном случае лишь один действительный корень. Его можно найти методом последовательных приближений, поскольку расчеты, связанные с решением кубического уравнения по общей формуле Кардано, весьма громоздки.

В качестве первого приближения вычислим молярный объем Vo1 газа, рассматривая его как идеальный. Тогда из уравнения состояния идеального газа получим

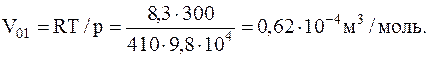
Теперь, обозначив в уравнении Ван-дер-Ваальса поправку на давление через p_o1=a/V_o², найдем величину V_o

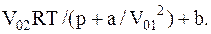
Взяв из таблиц значения постоянныхa и b для кислорода, выразим в единицах СИ входящие в формулу величины: p=410×9,8×10⁴ Па, V_o1=0,62×10^-4 м3/моль, R=8,3 Дж/(моль×К), Т=300 К, a=0,13 м⁴Н/моль², b=3,1×10^-5 м³/моль. Выполнив вычисление, найдем

V_o2=0,65×10^-4 м³/моль.

Еще раз вычислив по формуле, полученной изуравнения Ван дер Ваальса, считая при этом p₁=a/V_o2², получим третье приближение:

V_o3=0,66×10^-4 м³/моль.

Повторяя, таким образом, вычисления, будем получать все более точные значения V_o:

V_o4=0,67×10^-4 м³/моль;

V_o5=0,67×10^-4 м³/моль.

Видим, что при дальнейших вычислениях, если ограничиться точностью до второго знака, результат небудет изменяться. Еслиже взять значение V_o5=0,68×10^-4 м³/моль, то получим прежнее значение

V_o6=0,67×10^-4 м³/моль.

Поэтому, действительнымкорнемкубическогоуравнения Ван дер Ваальса, вычисленным с точностью до второго знака, будет

V_o=0,67×10^-4 м³/моль.

Теперь вычислим искомую массу газа

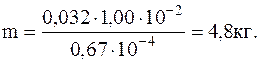
Легко убедиться в том, чтовычисление по уравнениюМенделеева-Клапейрона дало бы в этом случае неверный результат

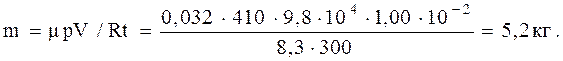
1.4.7. Какую часть объема стеклянной ампулы должен занимать жидкий эфир при t=20 ^oС, чтобы при его нагревании можно было наблюдать переход вещества через критическое состояние? Для эфира m=0,074 кг/моль, r=714 кг/м³ при 20 ^oС, t=194 ^oС, p=35,6 ат.

Решение. Переход вещества через критическое состояние характерен тем, что при этомисчезает различие междужидкойи газообразной фазами вещества. Критическое состояние характеризуется определенными для каждого вещества параметрами: критическими значениями температуры Т_к, давления p_к и молярного объема V_0к. При этом критический объем всей массы вещества, содержащей n=m/m молей, равен:

V_к=nV_0к=(m/m)V_0к.

Если вещество, нагретое до критической температуры T_к, окажется в объеме V, не равном V_к, то оно не будет при этом находиться в критическом состоянии. В этом случае при достижении температуры T_к не будет исчезать различие между двумя фазами, так как еще до достижения T_к все вещество при нагревании постепенно перейдет в одну фазу (при V>V_к вся жидкость в сосуде испарится, при V<V_к весь пар сконденсируется). Таким образом, для того чтобы наблюдать переход вещества, находящегося в ампуле, через критическое состояние, необходимо, чтобы при достижении критической температуры занимаемый им объем V был равен критическому объему V_к.

Так как в этот момент вещество будет равномерно заполнять всю ампулу, то V является одновременно и объемом ампулы.

Искомое отношение объема V_ж жидкого эфира к объему V ампулы найдем из ранее написанных уравнений, с учетом того, что m/V_ж=r – плотность жидкого эфира:

V_ж/V=V_ж/V_к=mV_ж/(mV_ок)=m/rV_oк.

Выразив величину V_ок через известные p_к и T_к получим

T_к/p_к=8a×27b²/(27bRa)=8b/R;

V_ок=3b=3RT_к/8p_к.

Окончательно для искомого отношения имеем:

V_ж/V=8mp_к/(3RrT_к).

Выразим в единицах СИ данные величины: m=0,074 кг/моль, p=35,6×9,8×10⁴ Па, r=714 кг/м³, Т_к=467 К. Подставив эти значения в формулу и выполнив вычисление, найдем

V_ж/V=0,25.