Примеры решения задач. 2.1. Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю теплоты

2.1. Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю теплоты, как и кирпичная стена, толщиной d=40 см при одинаковой температуре внутри и снаружи здания? Коэффициенты теплопроводности кирпича и дерева равны соответственно: c_к=0,70 Вт/(м×К), c_д=0,175 ВТ/(м×К).

Решение. Количество теплоты, переданное через площадь S за время t, если расстояние между плоскостями d, а разность температур между ними DT, равно

Q=cDTtS/d,

где c-коэффициент теплопроводности.

Запишем уравнение теплопроводности через стену для обоих материалов:

.

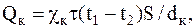
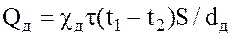Так как потеря теплоты должна быть одинаково, т.е. Q_к=Q_д, имеем

.

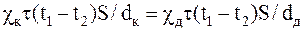Откуда толщина деревянной стены

d_д=d_кc_д/c_к.

Подставим в полученное соотношение числовые значения в единицах СИ, после вычислений, будем иметь

d_д=0,4×0,175/0,70=0,1 м.

2.2. Стена нагревательной печи толщиной d=0,75 м выполнена целиком из огнеупорного шамотного кирпича с коэффициентом теплопроводности c₁=1 Вт/(м×К). Какова будет толщина стены, если ее выполнить двухслойной, сохранив первый слой из того же материала толщиной d₁=0,25 м, а второй слой из неогнеупорного, но малотеплопроводного, материала, у которого коэффициент теплопроводности c₂=0,1 Вт/(м К)? Тепловой поток и температуры наружных поверхностей у двухслойной стены те же, что и у однослойной.

Решение. Тепловой поток – количество теплоты, переданное единичной площади в единицу времени, можно определить по формуле

где c – коэффициент теплопроводности;

DT-разность температур;

d – расстояние между двумяплоскостями.

Запишем уравнение теплового потока через однослойную стенуи через каждый из слоев двухслойной:

q₁=c₁(t₁-t₃)/d,

q₂=c₁(t₁-t₂)/d₁,

q₃=c₂(t₂-t₃)/d₂.

Из каждого соотношения выразим изменение температур

(t₁-t₃)=qd/c₁,

(t₁-t₂)=qd₁/c₁,

(t₂-t₃)=qd₂/c₂.

Складывая левые и правые части вышенаписанных формул, получим

2(t₁-t₃)=q(d/c₁+d₁/c₁+d₂/c₂).

Подставим в последнее выражение значение q для однослойной стены и, преобразовав, имеем

d₂=c₂(d-d₁)/ c₁.

Тогда общая толщина двухслойной стены будет равна:

d₃=d₁+d₂=d₁+c₂(d-d₁)/ c₁.

Подставив значения величин в единицах СИ, произведем вычисление

d₃=0,3 м.

2.3. Определить время подъема движущихся с постоянной скоростью пузырьков воздуха со дна водоема глубиной 1 м, если диаметры пузырьков соответственно равны 2 мм и 1 мм.

Решение. В рассматриваемом случае уравнение движения пузырьков имеет вид

ma=F+F_A+F_с,

где m-масса пузырька;

a – его ускорение;

F=mg – сила тяжести;

F_A – подъемная сила (сила Архимеда);

F_c – сила сопротивления ( сила внутреннего трения).

Так как движение пузырька равномерное, то, очевидно, сила сопротивления движению уравновешивается подъемной силой; силой тяжести можно пренебречь, так как плотность воздуха во много раз меньше плотности воды. Предполагая, что пузырек имеет небольшой радиус и сферическую форму, то согласно закону Стокса, силу сопротивления движению можно определить по формуле:

F_с=6phr,

где h – коэффициент вязкости;

r – радиус пузырька;

v – его скорость.

Подъемая сила

F_A=r_ogV=4pr³r_og/3,

где r_o-плотность воды;

g – ускорение силы тяжести.