Примеры решения задач. 1.3.1. Средняя квадратичная скорость молекул некоторого газа 450 м/с
1.3.1. Средняя квадратичная скорость молекул некоторого газа 450 м/с. Давление газа 50 кПа. Найти плотность газа при этих условиях.
Решение. Средняя квадратичная скорость молекул газа связана с его температурой соотношением
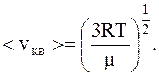
где R – универсальная газовая постоянная;
m – молекулярная масса газа;
T – абсолютная температура газа.
Для определения температуры газа воспользуемся уравнением Менделеева-Клапейрона
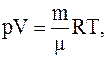
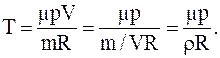
где r=m/V – плотность газа.
Следовательно
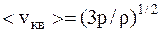 .
.
Откуда
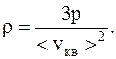
Подставляя численные значения имеем
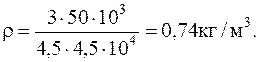
1.3.2. Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Эффективный диаметр молекул воздуха s=0,3 нм.
Решение. Средняя длина свободного пробега молекул газа
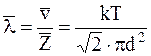 ,
,
где <v> – средняя арифметическая скорость молекул;
<Z> – среднее число столкновений каждой молекулы с остальными молекулами в единицу времени;
s – эффективный диаметр молекулы;
n – число молекул в единице объема (концентрация молекул). Для определения числа молекул в единице объема воспользуемся основным уравнением молекулярно-кинетической теории для давления
p=nkT,
где k – постоянная Больцмана;
Т – температура газа.
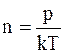 .
.
Тогда для средней длины свободногопробегаимеем
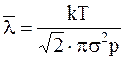 .
.
Подставляячисленные значения, окончательно получаем:
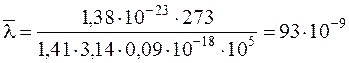 м.
м.
1.3.3. Найти среднее число столкновений в единицу времени молекул углекислого газа при температуре 100 oС, если средняя длина свободного пробега <l>=870 мкм.
Решение. Число столкновений молекул газа в единицу времени связаносо средней длиной свободного пробега соотношением
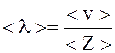 ,
,
где  – средняя арифметическая скорость.
– средняя арифметическая скорость.
Следовательно,

Подставляячисленные значения имеем
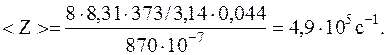
1.3.4. При некотором давлении и температуре 0 oС средняя длина свободного пробега молекул кислорода 95 нм. Найти среднее число столкновений в единицу времени молекул кислорода, если давление кислорода уменьшить в 100 раз.
Решение. Среднее число столкновений в единицу времени
 ,
,
где <v>=(8RT/pm)1/2 – средняя арифметическая скорость молекул газа;
<l> – средняя длина свободного пробега молекул.
При изменении давления газа длины свободного пробега обратно пропорциональныдавлению:
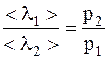 ,
,
где l1, l2 – длина свободного пробега молекул газа при соответствующих давлениях p1 и p2.
В нашем случае:
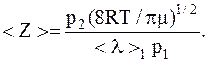
Подставляя численные значения для <Z>, имеем
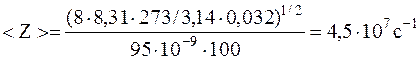 .
.
1.3.5. Какая часть молекул кислорода при t=0 oС обладает скоростями от 100 до 110 м/с?
Решение. Распределение молекул по скоростям можно определить из закона Максвелла
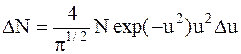 ,
,
где u=v/vв – относительная скорость;
v – данная скорость;
vв=(2RT/m)1/2 – наиболее вероятная скорость молекул;
Du – интервал относительных скоростей, малый по сравнению со скоростью u.
Тогда искомая часть молекул, которую необходимо определить (распределение молекул по скоростям)
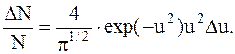
В нашем случае v=100 м/с; v=10 м/с; Наиболее вероятная скорость v=(2RT/pm)1/2=376 м/с. Следовательно, u=v/vв=100/376, u2=0,071; Du=10/376; exp(-u2)=0,93.
Тогда
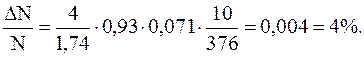
Таким образом, число молекул кислорода, скорости которых лежат в указанном интервале, равно 4%общего числа молекул.
1.3.6. Сосуд, содержащий газ, движется со скоростью vo, затем быстро останавливается. На сколько увеличится при этом средний квадрат скорости теплового движения молекул газа в случаях: одноатомного газа? Двухатомного газа? Газ считать идеальным.
Решение. Воспользуемся законом сохранения энергии. Пусть M-масса газа в сосуде. Двигаясь со скоростью v газ, как целое, обладает кинетической энергией
Wк=Mvo2/2.
Эта формула определяет кинетическую энергию направленного движения молекул, в котором ониучаствуют вместе с сосудом. После остановки сосуда направленное движение молекул в результате их соударений со стенками сосуда очень скоропревратится в хаотическое.
Пренебрегая теплообменом между газом и стенкамисосуда за рассматриваемый промежуток времени, можно газ считать изолированной системой. Тогда из закона сохранения энергии следует, что "исчезнувшая" кинетическая энергия направленного движения молекул W должна быть равна приросту энергии хаотического движения молекул (приросту внутренней энергии DU:
Wк=DU.
Определим внутреннюю энергию газа. Для идеального одноатомного газа это есть энергия поступательного хаотического движения молекул:
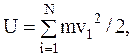
где m – масса молекулы;
N – число молекул в сосуде.
Имеем
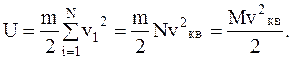
Отсюда следует, что изменение внутренней энергии одноатомного газа при торможении
DU=U2–U1=M[v2кв2-v2кв1]/2,
где vкв1,vкв2 – средние квадратичные скорости молекул газа соответственно в начале и конце торможения.
Подставив в уравнение Wк=DU значения Wк и DU, получим первый ответ
v2кв2-v2кв1=v2o.
Внутренняя энергия идеального двухатомного газа складывается из энергий поступательного и вращательного движения молекул. При этом три степени свободы приходятся на поступательное движение и две - на вращательное. В соответствии сзакономо равномерном распределении энергии по степенямсвободы, три пятых кинетической энергии W пойдет на увеличениеэнергии поступательного движения молекул и две пятых - на увеличение энергии их вращательного движения. Таким образом, теперь имеем
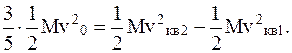
Откуда получим второй ответ:
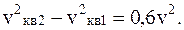
1.3.7. Какая часть молекул водорода, находящегося при температуре T, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше чем на 5,0 м/с? Задачу решить для двух значений T: 1) 400 К, 2) 900 К.
Решение. Распределение молекул по скоростям выражается законом Максвелла: число молекул DN, относительные скорости которых лежат в интервале от u до u+Du:

где N-полное число молекул газа;
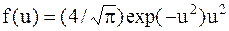 – функция распределения Максвелла;
– функция распределения Максвелла;
u=v/vв – относительная скорость;
v – данная скорость;
vв – наиболее вероятная скорость.
Закон распределения Максвелла оказывается справедливым при условии Du<u. Поскольку в задаче идет речь о наиболее вероятной скорости, надо считать v=vв. Следовательно, u=v/vв=1 и выше написанное уравнение примет более простой вид:
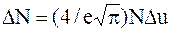 .
.
Отсюда найдем ту часть молекул, относительные скорости которых лежат в интервале Du:

Прежде чем производить расчеты, необходимо убедиться в том, что выполняется условие Du<u. Так как u=v/vв, то Du=Dv/vв.
Чтобы вычислить Du, найдем сначала наиболее вероятную скорость при Т=400 К и Т=900 К по формуле:
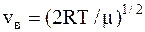
vв1=2×8,31×400/0,002=1,82×103 м/с,
vв2=2×8,31×900/0,002=2,73×103 м/с.
Подставляя эти значения vв и имея в виду, что Dv=10 м/с, поскольку в задаче идетречь о скоростях, лежащих в интервале от vв=-5,0 м/с до vв=+5,0 м/с, получим:
Du1=1/182, Du2=1/273.
Так как u=1, видим, что условие Du<u выполняется для обеих температур.
Теперь найдем
DN1/N=4/((3,14)1/2 ×2,7×182)=0,0046,
DN2/N=4/((3,14)1/2×2,7×273)=0,0030.
Таким образом, приувеличении температуры наиболее вероятная скорость молекул увеличивается,а числомолекул, скорости которых лежат в одном и том же интервале около наиболее вероятной, уменьшается.
1.3.8. Какая часть молекул газа имеет скорости превышающие наиболее вероятную скорость?
Решение. В условии задачи речь идет о молекулах, скорости которых заключеныв интервале от наиболеевероятной скорости vдо v+Dv, т.е. в бесконечно большом интервале скоростей v. Таким образом, условие применимости закона распределения скоростей, заключающееся в том, что Du<u, или Dv<v, здесь не выполняется. Поэтому от уравнения в форме:
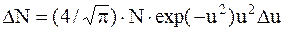
надо перейти к дифференциальнойформе этого закона
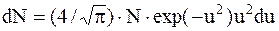 .
.
Полное число DN молекул, относительные скорости которых лежат в заданном интервале от u1 до u2, найдем, интегрируя правую часть в этих пределах:
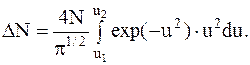
Дата добавления: 2014-12-30; просмотров: 8752;
