Из него

n_o=p/(kT).

Подставляя в ранее полученные формулы ы системе СИ для объема, парциальных давлений кислорода и азота и числа молекул в единице объема, имеем:

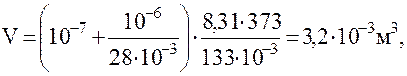
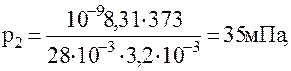
1.1.15. Один моль идеального 2-х атомного газа, занимает объем 12,3 л под давлением 2 ат. нагревается при постоянном объеме до давления 3 ат. Далее газ расширяется при постоянном давлении до объема 24,6 литра, после чего охлаждается при постоянном объеме до начального давления, и, наконец, сжимается при постоянном давлении до начального объема. Определить температуру газа для характерных точек цикла.

Решение.

Пусть V' – наименьший объем газа;

V" – наибольший объем газа;

p' – наименьшее давление газа;

p" – наибольшее давление газа;

T₁, T₂, T₃, T₄ – температуры газа в характерных точках.

Температуру T₁ можно найти, используя уравнение Менделеева-Клапейрона:

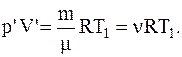
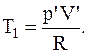
Переход газа из состояния 1 в состояние 2-изохорный, для которого справедливо соотношение:

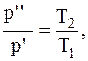
откуда

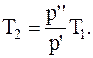
Переход газа из состояния 2 в состояние 3-изобарный, для которого справедливо соотношение:

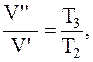
откуда

Переход газа из состояния3 в состояние 4-изохорный, для которого справедливо соотношение

откуда

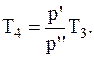
Подставляя численные значения из условия задачи, будем иметь:

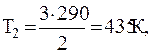
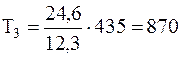К,

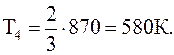
1.1.16. Плотность смеси азота и водорода при температуре t=47 ^oС и давлении p=2,00 ат равна 0,30 г/л. Найти концентрации молекул азота (n₁) и водорода (n₂) в смеси.

Решение. Концентрацию однородного по составу газа можно найти из формулы

p=n_okT.

В условии задачи дана смесь двух газов, молекулы которых различаются по массе. Приведенная формула является следствием основного уравнения кинетической теории газов

p=(2/3)n_o<W_к>,

где n_o – число молекул в единице объема (концентрация молекул);

<W_к>=<mV²>/2 – средняя кинетическая энергия поступательного

движения одной молекулы газа.

Для однородного по составу частиц газа

<W_к>=mV²/2.

Из вывода основного уравнения кинетической теории газов вытекает, что оно справедливо для совокупности любых частиц, в том числе различных по массе. Следовательно, формулу p=n_okT можно применять для смеси газов. В этом случае n_o-полное число частиц в единице объема. Таким образом, имеем

n_o=p/kT.

Для определения концентрации азота и водорода кроме очевидного соотношения

n₁+n₂=n_o=p/kT

необходимо иметь еще одно уравнение, связывающее величины n₁ и n₂.

Используя данные задачи, можно найти молярную массу m_см смеси рассматриваемых газов, пользуясь уравнением Менделеева-Клапейрона

pV=mRT/m_см

или

p=rRT/m_см,

откуда

m_см=rRT/p.

С другой стороны, можно выразить m_см через молярные массы азота (m₁) и водорода (m₂), а также их концентрации n₁ и n₂, записав уравнение газового состояния для каждого из газов входящих в смесь

pV=m×RT/m_см,

p₁V=m₁RT/m₁,

p₂V=m₂RT/m₂.

Откуда

p=m×RT/(m_cvV),

p₁=m₁RT/(m₁V),

p₂=m₂RT/(m₂V).

На основании закона Дальтона, давление смеси газов равно сумме парциальных давлений

p=p₁+p₂.

Имеем

p=m₁RT/m₁V+m₂RT/m₂V=(m₁/m₁+m₂/m₂)RT/V,

где (m₁/m₁+m₂/m₂)=(m₁+m₂)/m_см, т.е. для молярной массы смеси азота и водорода получаем

m_см=m₁m₂(m₁+m₂)/(m₁m₂+m₂m₁).

Заметим также, что между массой m газа и его концентрацией n существует связь:

m=nVm'=nVm/N_А,

где V – объем газа;

m – его молярная масса;

m' – масса одной молекулы;

N_А – число Авогадро.