Окончательно

d=(m/(pN_А))^1/3.

Произведем вычисления

1.1.4. В баллоне объемом 10 л находится гелий под давлением p₁=1 МПа и при температуре T=300 К. После того как из баллона было взято m=10 г гелия,температура газа понизилась до Т=290 К Определить давление p гелия оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его дважды к начальному и конечному состояниям газа:

;

,

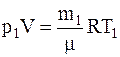где m₁, m₂ – массы гелия в баллоне в начальном и конечном состояниях;

m – молярная масса гелия;

R – универсальная газовая постоянная;

T₁ и T₂ – температуры газа в начальном и конечном состояниях.

Массы m₁ и m₂ гелия найдем из уравнения Менделеева-Клапейрона:

m₁=p₁mV/(RT₁),

m₂=mp₂V/(RT₂).

Тогда масса гелия оставшегося в баллоне будет равна

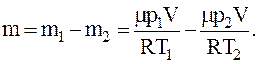
Для давления p гелия, оставшегося в баллоне, будем иметь:

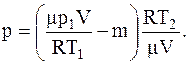
или

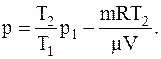
Численно

.

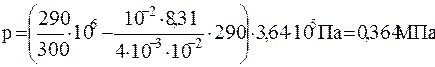1.1.5. Баллон содержит 80 г кислорода и 320 г аргона. Давление смеси 1МПа, температура 300 К. Принимая данные газы за идеальные, определить объем баллона.

Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. Парциальные давления кислорода p₁ и аргона p₂ можно определить, воспользовавшись уравнением Менделеева-Клапейрона

p₁=m₁RT/(m₁V), p₂=m₂RT/(m₂V).

Следовательно, по закону Дальтона, давление смеси газов

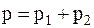или

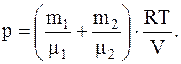
Откуда объем баллона

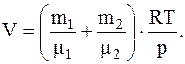
Подставив численные значения, будем иметь

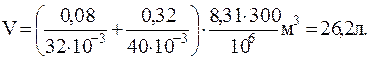
1.1.6. Какое количество молекул находится в комнате объемом 80 м³ при температуре 17 ^oС и давлении 750 мм. рт. ст?

Решение. Количество молекул N, содержащееся в комнате, можно определить, зная массувоздуха m,его молярную массу и число Авогадро N_А. Число молекул в одном киломоле газа равно числу Авогадро. А число киломолей содержащихся в массе m, определяется соотношением:

n=m/m.

Следовательно,

N=m/(mN_А).

Массу m содержащегося в комнате воздуха определяем из уравнения Менделеева-Клапейрона

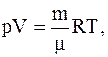
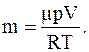
где p – давление воздуха;

V – объем;

R – универсальная газовая постоянная;

T – абсолютная температура (T=t+ 273 );

m – масса воздуха.

Следовательно, для числа молекул воздуха имеем:

Подставляя все данные, предварительно выразив их в системе СИ, будем иметь

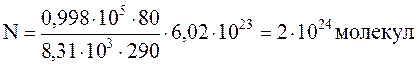
1.1.7. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре T=350 К, а также кинетическую энергию вращательного движения всех молекул кислорода массой 4 г.

Решение. Согласно теореме о равномерном распределении энергии по степеням свободы, накаждую степень свободы приходится энергия:

,

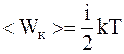где k – постоянная Больцмана;

Т – абсолютная температура.

Молекула кислородадвухатомная, поведение такой молекулы описывается 5-ю степенями свободы (три изних приписываются поступательному движению и две- вращательному).

Следовательно, кинетическая энергия вращательного движения молекулы кислорода может быть рассчитана по формуле:

<Wвр>=2 <Wк>=2×1/2 kТ=kТ.

Энергия вращательного движения всех молекул, содержащихся в 4 г кислорода, может быть определена как произведение числа молекул N на энергию одной молекулы:

Wк=N×<Wвр>=NkТ.

Число молекул определяется соотношением:

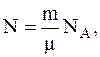
где m – молекулярная масса кислорода;

m – его масса;

N_А – число Авогадро.

Таким образом

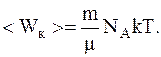
Подставив численные значения, предварительно выразив их в системе СИ, будем иметь:

<W_вр>=1,38×10^-23.350=4,83×10^-21 Дж;

.

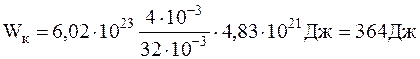1.1.8. Масса 10 г кислорода находится при давлении 304 кПа и температуре 10 ^oС. После расширения вследствие нагревания при постоянном давлении кислород занял объем 10 л. Найти объем газа до расширения, температуру газа после расширения, плотности газа до и после расширения.

Решение. Согласно условию задачи, расширение газа вследствие нагревания происходило при постоянном давлении. В этом случае оказывается справедливым соотношение

.

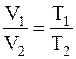Для определения температуры газа после расширениявоспользуемся уравнениемМенделеева-Клапейрона для конечного состояния газа

,

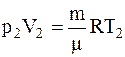где p₂ – давление газа после расширения;

V₂ – его объем после расширения;

m – масса газа;

m – молекулярная масса кислорода;

R – универсальная газовая постоянная;

T₂ – абсолютная температура газа.

Следовательно, дляконечной температуры имеем

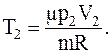
Для определения объема газа до расширения можно вновь воспользоваться уравнением Менделеева-Клапейрона, записанным для первоначального состояния газа:

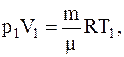
где p₁, V₁, T₁ – его давление, объем и температура до расширения.

Из данногоуравнения имеем

.

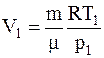Учитывая то, что плотность газа r₁=m/V₁, подставляя значения V₁ и V₂ из уравнений Менделеева-Клапейрона, записанные для соответствующих состояний, для плотности кислорода до и после расширения будем иметь

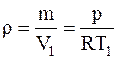и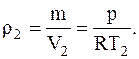

Подставляя численные значения в системе СИ, окончательно имеем:

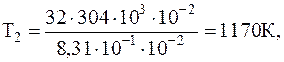
r₁=4,14 кг/м³,

r₂=1кг/м³.

1.1.9.Масса газа 12 г занимает объем 4 л при температуре 7 ^oC. После нагревания газа при постоянном давлении его плотность стала равной 0,6 кг/м³. До какой температуры нагрели газ?

Решение. Воспользовавшись уравнением Менделеева-Клапейрона

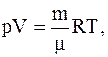
можно показать, что между плотностью газа r=m/V и давлением существует связь

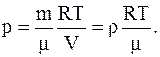
Следовательно, в начальномсостоянии давление газа:

В конечном:

Так как нагревание газа производилось при постоянном давлении, то p₁=p₂

.

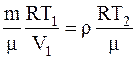Отсюда

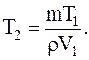
Подставляя численные значения, в системе СИ, для конечной температуры будем иметь:

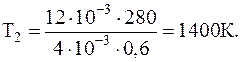
1.1.10. В баллоне находилась масса m₁=10 кг газа при давлении p₁=10 МПа. Какую массу газа взяли из баллона, если давление стало равным p₂=2,5 МПа? Температуру газа считать постоянной.

Решение. Запишем уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) для двух состояний: начального и конечного

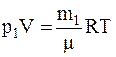и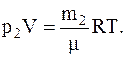

Из второгосоотношения определяем объем сосуда и подставляем его значение в первое, имеем:

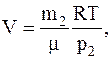
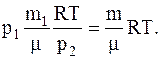
Из последнего соотношения получаемсвязь между давлением газа в сосуде и его массой для данного случая:

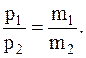
Отсюда масса газа оставшегося в баллоне:

.

Так как масса израсходованного газа Dm=m₁-m₂,то окончательно, после соответствующих преобразований, имеем

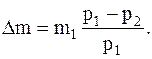
Подставляячисленные значения в системе СИ определяем массу взятого из баллона газа:

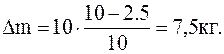
1.1.11. В сосуде находится масса m₁=14 г азота и масса m₂==9 г водорода при температуре 10 ^oС и давлении 1 МПа. Найти молярную массу смеси и объем сосуда.

Решение. По закону Дальтона давление смеси газов равно сумме парциальных давлений компонентов входящих в смесь

p=p₁+p₂,

где p – давление смеси;

p₁ – парциальное давление азота;

p₂ – парциальное давление водорода.

Из уравнения Менделеева-Клапейрона:

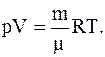
Для каждого из давлений (смеси и парциальных) можно записать:

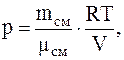
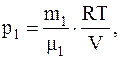
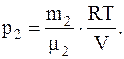
Следовательно, так как p=p₁+p₂, имеем

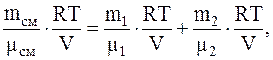
откуда

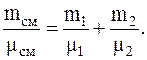
Из последнего соотношения для молекулярной массы смеси будем иметь

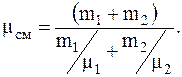
Изуравнения Менделеева-Клапейрона, для смеси газов, объем сосуда равен:

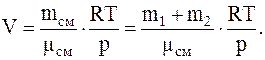
Подставляячисленные значения в системе СИнаходиммолекулярную массу смеси:

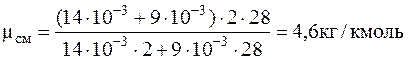
и объем сосуда

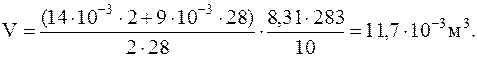
1.1.12. Для получения хорошего вакуума в стеклянном сосуде необходимо прогревать стенки сосуда при откачке для удаления, адсорбированного газа. На сколько может повыситься давление в сферическом сосуде радиусом 10 см, если адсорбированные молекулы перейдут со стенок в сосуд? Площадь поперечного сечения молекул S_o==10^-19 м². Температура газа в сосуде 300 ^oС. Слой молекул на стенках считать мономолекулярным.

Решение. Для определения давления воспользуемся основным уравнением молекулярно-кинетической теории в виде

p=n_okT,

где n_o – число молекул в единице объема;

k – постоянная Больцмана;

Т – абсолютная температура газа.

С учетом того, что

n_o=N/V,

где N – число молекул в объеме V, для давления имеем

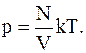
Поусловиюзадачи слой молекул в сосуде мономолекулярный, следовательно число молекул в нем можно определить исходя из соображений:

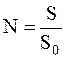
где S=4pr² – площадь поверхности сосуда;

S_o – площадь поперечного сечения молекул газа.

Так как сосуд сферический, то его объем V=4/3pr³.

Таким образом, окончательно для давления газа в сосуде будем иметь соотношение:

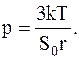
Подставляячисленные значения в полученноесоотношение в системе СИ определяем давление газа в сосуде

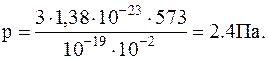
1.1.13. В воздухе содержится 23,6 % кислорода и 76,4 % азота (по массе) при давлении 100 кПа и температуре 13 ^oС. Найти плотность воздуха и парциальные давления кислорода и азота.

Решение. Для определения плотности воздуха воспользуемся уравнением Менделеева-Клапейрона

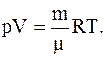
откуд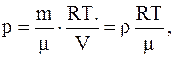а

а .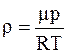

Для определения парциальных давлений также воспользуемся уравнением Менделеева-Клапейрона, записанным для каждого из компонентов, входящих в смесь воздуха:

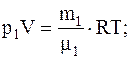
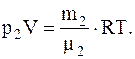
где V – объем воздуха.

Откуда

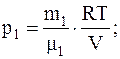
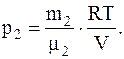
Так как r=m/V, то V=m/r, следовательно

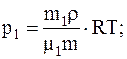
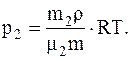
Подставляячисленные значения в системе СИ для плотности воздуха и парциальных давлений кислорода иазота будем иметь:

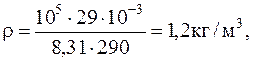
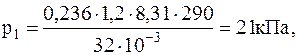
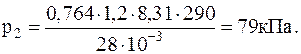
1.1.14. В сосуде находится количество n=10^-7 моль кислорода и масса m₂==10^-6 г азота. Температура смеси 100 ^oС, давление в сосуде p=133 мПа. Найти объем сосуда, парциальные давления кислорода и азота и число молекул в единице объема.

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, записанным для смеси газов в виде

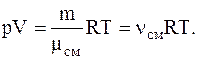
где n_см=n₁+n₁=(n₁+m₂/m₂) – число молей или киломолей газов составляющих смесь.

Имеем

pV=(n₁+m₂/m₂) RT.

Отсюда

V=(n₁+m₂/m₂) (RT/p).

Парциальные давления компонентов образующих смесь определяем так же из уравнения Менделеева-Клапейрона, записанным для каждого из газов

p₁V=n₁RT и p₂V =(m₂/m₂)RT.

Откуда для парциальных давлений кислорода и азота соответственно имеем

p₁=n₁RT/V;

p₂=m₂RT/m₂V.

Для определения числа молекул в единице объема необходимо воспользоваться основным уравнением молекулярно-кинетической теории для давления

p=n_okT.