Рейс дальностью 5000 миль 1 страница
Судно с однородным грузом в трюмах (m = 1.487 м3/т)
при осадке по летнюю грузовую марку (отход)
| Статья нагрузки | P, т | Z, м от ОЛ | Mz , тм | X, м от Ä | Mx, тм | Попр. dMz, тм | ||
| Судно порожнем | 7261.9 | 10.09 | -13.82 | -100383 | ||||
| Экипаж, провизия, снабжение | 11.5 | -476 | ||||||
| Танк 1.20 расх.кот. топ. ПрБ Танк 1.22 расходный ДП | 1.50 52.7 | 11.85 11.33 | -36.57 -36.42 | -55 -1919 | ||||
| Танк 2.6 расходный ЛБ | 7.7 | 11.33 | -36.77 | -283 | ||||
| Танк утечн. масла 3.2 ПрБ Танк сепарир.масла 3.3 ЛБ Танк сепарир.масла 3.4 ПрБ Танк сточн. масла 3.5 ДП Танк утечн. масла 3.7 ЛБ Танк отработ.масла 3.8 ДП Танк цилинд.масла 3.9 ПрБ Танк запасн.масла 3.10 ПрБ Танк запасн масла 3.11 ПрБ | 0.5 7.2 7.2 16.0 2.0 5.9 3.7 10.4 5.2 | 0.75 0.50 0.62 0.95 1.16 0.35 10.70 11.13 10.85 | 5.6 | -53.45 -46.00 -46.24 -47.83 -53.45 -57.35 -65.30 -65.14 -69.10 | -27 -331 -333 -765 -107 -338 -242 -677 -359 | |||
| Танк охлажд. воды 4.1 ЛБ Танк кот. питат. в. 4.2 ПрБ Танк кот.питат. в. 4.3 ЛБ Танк питьевой воды 4.6 ДП Танк охлажд. воды 4.8 ДП | 17.1 57.8 57.8 24.0 | 0.98 7.25 7.25 11.74 3.00 | -40.94 -57.96 -57.96 -66.03 -62.81 | -700 -3350 -3350 -1585 -151 | ||||
| Фекальный танк 3.12 ЛБ Танк гр. в. мед. бл. 3.16 ЛБ | 7.9 2.1 | 11.37 11.86 | -36.14 -24.84 | -286 -52 | ||||
| Трюм 1 низ Трюм 1 середина Трюм 1 верх Трюм 2 низ Трюм 2 середина Трюм 2 верх Трюм 3 низ Трюм 3 середина Трюм 3 верх Трюм 4 низ Трюм 4 середина Трюм 4 верх | 492.0 542.0 721.0 755.0 701.0 779.0 909.0 782.0 849.0 845.0 780.0 861.0 | 3.78 7.21 11.46 3.73 7.18 11.42 3.69 7.18 11.42 3.72 7.18 11.42 | 40.86 41.73 41.88 22.43 23.03 22.97 -4.46 -4.81 -4.65 -24.37 -24.93 -24.87 | -4054 -3761 -3948 -20593 -19445 -21413 | ||||
| Груз на палубе | 0.0 | 0.0 | 0.0 | |||||
| Всего балласта | 0.0 | |||||||
| Водоизмещение | 17375.3 | 8.62 | -5.25 | -91296 | ||||
| Всего поправка dMz, тм | ||||||||
| Момент Mz расчетный, тм | ||||||||
| ЦМ судна Zg расчетный, м | 8.79 | |||||||
| ЦМ судна Zg допустимый, м | 9.11 | |||||||
| Аппликата метацентра Zm, м | 9.33 | |||||||
| Метацен-трическая высота | Без поправки ho = Zm - Zg, м Поправка dh, м Исправленная h = ho - dh, м | 0.64 К*=3.15 0.10 0.54 | ||||||
| Осадка | Средняя dср, м Носом dн, м Кормой dк, м | 7.94 6.92 8.96 | ||||||
Рис. 2.3.
2.3 Расчет объемного водоизмещения и координат центра величины судна
Значение объемного водоизмещения и его распределение по длине и высоте судна характеризуют строевые по шпангоутам и ватерлиниям, представленные на рис. 2.4.
Строевая по шпангоутам (рис. 2.4,а) представляет собой огибающую площадей шпангоутов в координатах х – А, вычисленных для заданной ватерлинии. Площадь, ограниченная строевой, соответствует объемному водоизмещению Ñ, абсцисса ЦТ этой площади – величине хс. Величина объемного водоизмещения и абсцисса ЦВ определяются выражениями
Ñ =  ; хс = (1/Ñ)
; хс = (1/Ñ) 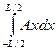 . (2.4)
. (2.4)
Входящие в выражения определенные интегралы вычисляют по правилам приближенного интегрирования. Используя способ трапеций, получаем
Ñ = dL[A1 + A2 + ... + A19 + ½(A0+ A20)]; (2.5)
xc = [(dL)2/Ñ][9,5(A0 - A20) + 9(A1 – A19) +...+ (10 – n) (An - A20-n)]. (2.6)
Приведенные выражения соответствуют использованию 21 теоретического шпангоута и, соответственно, размер теоретической шпации dL = L/20.
Строевая по ватерлиниям (рис. 2.3, б) представляет собой огибающую площадей ватерлиний в координатах z - S. Площадь, ограниченная строевой, соответствует объемному водоизмещению Ñ, аппликата ЦТ этой площади – величине zс. Величина объемного водоизмещения и абсцисса ЦВ определяются выражениями
Ñ = 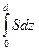 ; zс = (1/Ñ)
; zс = (1/Ñ)  . (2.7)
. (2.7)
Используя способ трапеций для вычисления определенных интегралов, входящих в приведенные выражения, получаем
Ñ = dd[S1 + ... + Sm-1 + ½(S0+ Sm)];
zc = [(dd)2/Ñ][S1 + 2S2 + ... + (m – 1)Sm-1 +(S0 + (2m –1)Sm)/4]. (2.8)
В приведенных выражениях d d = d/m – расстояние между соседними ватерлиниями.
Для определения объемного водоизмещения Ñ и абсциссы ЦВ хс судна с дифферентом используют различные диаграммы. Наиболее распространенной диаграммой является масштаб Бонжана (рис. 2.5), представляющий собой совокупность интегральных кривых площадей шпангоутов A(z), рассчитанных для 21 теоретического шпангоута для значений z от 0 до zmax, соответствующего палубе переборок.
                   а) А
An+1
An
An-1
20 0 X
L/2 L/2
Ä а) А
An+1
An
An-1
20 0 X
L/2 L/2
Ä
| б) z Sm Sm-1 d S2 S1 0 S |
Рис. 2.4. Строевые по шпангоутам (а) и ватерлиниям (б)
| А16 | А14 | dн |
Рис. 2.5. Масштаб Бонжана
Для определения Ñ и хс на масштабе Бонжана необходимо провести ватерлинию и отметить точки ее пересечения с линиями теоретических шпангоутов. Площади шпангоутов Ai снимаются по горизонтали и представляют собой расстояние от точки пересечения ватерлинии с линией шпангоута до соответствующей интегральной кривой. Подставляя снимаемые с масштаба Бонжана значения Ai в выражения (2.5) и (2.6), получают искомые Ñ и хс.
2.4 Гидростатические кривые
Гидростатические кривые или кривые элементов теоретического чертежа представляют собой совокупность кривых водоизмещения D, объемного водоизмещения Ñ, координат ЦВ xc и zc, площади ватерлинии S, абсциссы ЦТ площади ватерлинии xf, моментов инерции площади ватерлинии Ix и Iyf, метацентрических радиусов r и R, коэффициентов полноты корпуса a, b и CB, выражающих зависимость соответствующих параметров от осадки судна d. Шкала осадки располагается вдоль горизонтальной оси диаграммы.
В некоторых случаях указанные параметры приводятся в виде таблицы, называемой таблицей гидростатических элементов. Общий вид гидростатических кривых показан на рис. 2.6. Масштабы кривых выбирают исходя из обеспечения необходимой точности и удобства их использования в практических расчетах.
Совокупность кривых Ñ и zm называют метацентрической диаграммой, а зависимость D = f(d) – грузовым размером.

           xc xf r zc R S Ñ D b a CB xc xf r zc R S Ñ D b a CB
|
 КВЛ КВЛ
|
 0 d, м
0 d, м
Рис. 2.6. Гидростатические кривые
3 Остойчивость
Остойчивостью называется способность судна, наклоненного внешним воздействием, возвращаться в исходное положение после прекращения воздействия, вызвавшего наклонение.
Различают остойчивость поперечную и продольную, статическую и динамическую, начальную и остойчивость при больших наклонениях.
Если говорят остойчивость без определения, то предполагают начальную статическую поперечную остойчивость и/или ее показатель – начальную поперечную метацентрическую высоту.
3.1 Начальная остойчивость
3.1.1 Схема образования восстанавливающего момента
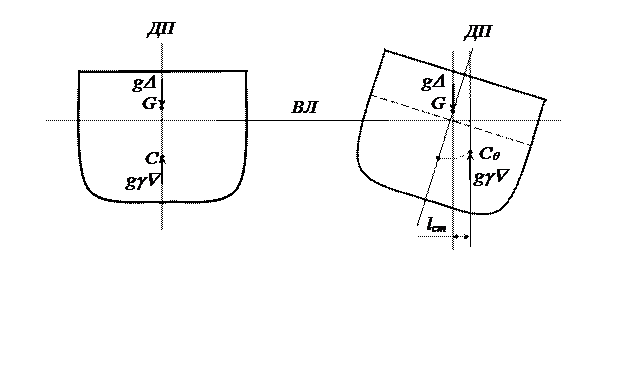
Рассмотрим малое поперечное равнообъемное наклонение судна (наклонение, в процессе которого водоизмещение судна не изменяется). Схема образования восстанавливающего момента при наклонении судна показана на рис. 3.1 (рис.3.1, а – судно в прямом положении; б – в наклонном положении; в – схема наклонения).
Предположим, что в исходном положении крен отсутствует, а для простоты изображения на схеме показываем наклонение ВЛ.
В начальный момент судно находилось в равновесии под действием сил тяжести и поддержания gD = grÑ, находившихся на одной линии. Под воздействием внешнего кренящего момента Мкр судно наклонилось на угол крена q, при этом ЦВ сместился в сторону наклонения и сила поддержания совместно с силой тяжести создали восстанавливающий момент Мв, равный по величине кренящему моменту Мв= Мкр. Равенство кренящего и восстанавливающего моментов выражает основной закон статических наклонений. Смещение ЦВ в сторону наклонения обусловлено тем, что при наклонении судна один борт (в приведенной схеме – правый) погружается в воду, а другой (левый) выходит из воды, это приводит к перераспределению погруженного объема корпуса судна и как следствие, смещение центра тяжести объема.
Согласно теореме Эйлера ось малого равнообъемного наклонения проходит через ЦТ площади действующей ВЛ. Поскольку на приведенной схеме в начальный момент крен отсутствовал, то в силу симметрии корпуса ЦТ площади действующей ВЛ находился в ДП, в этой точке пересекаются ватерлинии судна ВЛ и ВЛq. При малых наклонениях кривую центра величины ССq можно заменить дугой окружности радиуса r, называемого начальным поперечным метацентрическим радиусом, центр этой окружности находится в точке m, которая называется начальным поперечным метацентром.
а) б)
в)
|


|


|



|

|

|





|




|









 Z
Z
|
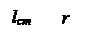 | |||
| |||
|
|
 ВЛ
ВЛ
|
 ВЛq
ВЛq
Мв
|
Рис. 3.1
Возвышение метацентра над центром тяжести называется начальной поперечной метацентрической высотой (МЦВ) h = zm - zg. Возникший при наклонении восстанавливающий момент как момент пары сил (тяжести и поддержания) равен произведению одной из сил на плечо, равное кратчайшему расстоянию между линиями действия этих сил. Это плечо обозначается lст и называется плечом статической остойчивости или плечом восстанавливающего момента. Восстанавливающий момент Мв = lстgD (кНм) илив размерности [тм] Мв = lстD. Из прямоугольного треугольника при m lст = h sinq. В итоге получаем метацентрическую формулу поперечной остойчивости
Мв= D h sinq, тм. (3.1)
Поскольку наклонения малы, что соответствует малым значениям угла крена q, можно воспользоваться известными математике соотношениями, справедливыми для малых углов, выраженных в радианах (радиан – единица безразмерная) sinq » q = q°/57,3°; cosq » 1,0 и получить метацентрическую формулу поперечной остойчивости в окончательном виде
Мвq = 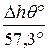 , тм. (3.2)
, тм. (3.2)
Приведенное выражение показывает линейную зависимость восстанавливающего момента от угла крена. При положительных значениях МЦВ (точка m расположена выше точки G) восстанавливающий момент положителен; при h = 0 (точки m и G совпадают) восстанавливающий момент равен нулю и судно остойчивостью не обладает; при отрицательных значениях МЦВ (точка m расположена ниже точки G) возникающий при наклонении судна момент увеличивает кренящий момент. Таким образом, знак и величина восстанавливающего момента определяется знаком и величиной МЦВ, и поэтому МЦВ используется в качестве показателя начальной остойчивости судна. Произведение Dh называется коэффициентом поперечной остойчивости.
Схема образования восстанавливающего момента при продольном наклонении показана на рис. 3.2. В общем случае, в силу большой величины отношения длины судна к его осадке, любые продольные наклонения можно считать малыми, поэтому все допущения, примененные при рассмотрении поперечных наклонений, применимы для продольных наклонений. Продольный метацентр обозначается M, его координаты – xM и zM, МЦ радиус – R, продольная МЦВ – H = zM - zg. Точкой F на схеме обозначен ЦТ площади действующей ВЛ. Выражение 3.1 для продольных наклонений записывается в виде
Мвy = DHsiny, тм.
Поскольку на практике в качестве параметра продольного наклонения используется величина дифферента, а не его угол, то по рис. 3.2 можно определить, что tg y = Df /L. Поскольку угол y мал, то в силу свойств малых углов sin y » tg y, а выражение продольного восстанавливающего момента имеет вид
Мвy =  , тм. (3.3)
, тм. (3.3)
Основной закон статических наклонений для продольных наклонений выражается равенством дифферентующего момента Мдиф и продольного восстанавливающего момента Мвy.
Выражение (3.3) называется метацентрической формулой продольной остойчивости, а произведение DH - коэффициентом продольной остойчивости.

 |

| |||||
| |||||
 |

|
|
|

 |


 |

Дата добавления: 2014-12-29; просмотров: 760;















































 dк
dк