Рейс дальностью 5000 миль 3 страница
d h = - lпР/D. (3.25)
 |








 |

 | |||||
 | |||||
 |

 | |||
 |
Рис. 3.8. Подвешенный груз
3.2.4 Жидкий груз со свободной поверхностью
В качестве жидкого груза рассматривается только жидкость в судовом помещении (цистерне, трюме), имеющая свободную поверхность. Если свободная поверхность отсутствует, как, например, в запрессованном танке, то жидкость рассматривается как твердый груз.
Если на судне имеется жидкий груз, то при наклонениях судна жидкость за счет свободной поверхности перетекает в сторону наклонения и создает дополнительный кренящий момент. Таким образом, жидкость в судовых помещениях, имеющая свободную поверхность, ухудшает остойчивость.
На рис. 3.9 показан отсек с жидкостью со свободной поверхностью. Цифрами 0 – 0 обозначена поверхность и буквой f - ЦТ жидкости в отсеке в прямом положении судна, цифрами 1 – 1 и буквой f1 – то же при крене судна
q. Если обозначить буквой а точку пересечения линий действия силы тяжести, приложенной к жидкости, то по аналогии с подвешенным грузом остойчивость судна изменится на величину
d h = - afР/D = af vgж/D, (3.26)
где Р, v и gж – масса, объем и плотность жидкости в отсеке.
Смещение ЦТ жидкости в отсеке аналогично перемещению ЦВ судна при малых наклонениях. По формуле для метацентрического радиуса судна (3.8) af = ix /v, где ix – момент инерции площади свободной поверхности жидкости в отсеке относительно продольной оси. Подставив af в выражение (3.26), получим формулу поправки на свободную поверхность
d h = - ixgж /D. (3.27)
Из приведенного выражения следует, что поправка на свободную поверхность зависит от момента инерции площади поверхности, плотности жидкости в отсеке, водоизмещения судна и не зависит от количества жидкости в отсеке. 






















Рис. 3.9. Жидкий груз со свободной поверхностью
В Информации об остойчивости судна для судовых цистерн приводятся значения поправки на свободную поверхность в виде поправки к моменту водоизмещения относительно ОП, рассчитанные с учетом плотности жидкости, для перевозки которой предназначена цистерна,
d mz = ixgж. (3.28)
Поскольку при больших наклонениях площадь свободной поверхности изменяется существенно, то в Информации об остойчивости могут быть приведены значения поправок на свободные поверхности для значений угла крена 0°, 30° и 60°, обозначаемые, соответственно, d mz0, d mz30 и d mz60.
Если цистерна заполнена жидкостью почти полностью или жидкости очень мало, то при наклонениях площадь свободной поверхности существенно уменьшается и поправка на свободную поверхность не существенна. Эти случаи называются недейственной потерей остойчивости. По Правилам Регистра цистерна, заполненная менее, чем на 5%, считается пустой, а более чем на 95% - запрессованной, и в этих случаях поправки на свободную поверхность не учитываются.
3.3 Остойчивость при больших наклонениях
При больших наклонениях кривую центра величины нельзя заменить дугой окружности, поскольку возникающие от подобной замены погрешности неприемлемы для практических расчетов. Поэтому при больших наклонениях используется другой способ расчета плеча статической остойчивости.
На рис. 3.10 представлена схема поперечного наклонения судна на угол, для которого замена кривой центра величины дугой окружности недопустима. Точка mq является центром кривизны кривой ССq в точке Сq.
Пользуясь обозначениями, приведенными на рис. 3.10, плечо статической остойчивости lст, выраженное отрезком GK, определяется выражением
GK = CB + BF – CA.
Выразив входящие в выражения отрезки через координаты ЦТ и ЦВ в прямом положении и при крене q, получим искомое выражение плеча статической остойчивости
lст = y сosq + (z – zc) sinq - (zg – zc) sinq. (3.29)
В выражении (3.29) первые два слагаемые выражают расстояние от ЦВ т. С до линии действия силы поддержания судна с креном и включают в себя координаты ЦВ судна при крене q, зависящие от формы корпуса, поэтому их сумма называется плечом формы lф = y cosq + (z – zc) sinq; последнее слагаемое выражает расстояние от т. С до линии действия силы тяжести судна с креном и зависит от водоизмещения и координат ЦТ судна, поэтому называется плечом веса lв= (zg – zc) sinq.
Выражение (3.29) принимает вид
lст = lф - lв. (3.30)
Если плечо статической остойчивости определять относительно т. 0, то плечо формы выражается отрезком 0М и обозначается lф* - расстояние от т. 0 до линии действия силы поддержания, а плечо веса будет равно lв* = zg sinq - расстояние от т. 0 до линии действия силы тяжести и, таким образом, выражение (3.30) будет иметь вид
lст = lф* - lв*. (3.31)



|
|





|
|
|
|
|
| |
|






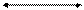










Рис. 3.10. Схема большого наклонения
3.4 Диаграмма статической остойчивости
Диаграмма статической остойчивости (ДСО) представляет собой графическую зависимость плеча статической остойчивости или восстанавливающего момента от угла крена.
Поскольку корпус судна симметричен относительно ДП, ДСО имеет две симметричные относительно точки 0 диаграммы ветви, однако изображается только одна – правая ветвь (рис. 3.11).
Поскольку ДСО является графическим изображением выражения lст = lф - lв, то для конкретного судна заданным значениям водоизмещения D и аппликаты ЦТ zg соответствует единственная кривая ДСО, для которой восстанавливающий момент Мв = lстD, тм.
3.4.1 Точки диаграммы статической остойчивости
При симметричной относительно ДП загрузке судна (yg =0) ДСО проходит через т. 0.
Максимум диаграммы lmax показывает максимальный восстанавливающий момент Мвmax = lmaxD, соответствующий данной загрузке; этот момент называется статическим опрокидывающим моментом Мсст - судно может быть опрокинуто только кренящим моментом, превосходящим по величине Мсст.
Максимуму диаграммы соответствует угол максимума qm, делящий ДСО на восходящую (0 < q < qm) и нисходящую ветви (qm < q < qv). Для того, чтобы определить, как ведет себя судно, находясь на той или иной ветви, на ДСО проведем линию, соответствующую действию постоянного статического кренящего момента. Эта линия имеет две точки пересечения с диаграммой, соответствующие равенству кренящего и восстанавливающего моментов (Мкр = Мв).













Рис. 3.11. Диаграмма статической остойчивости
Рассмотрим, как ведет себя судно, находящееся в положении равновесия на восходящей (т. 1) и нисходящей (т. 2) ветвях. Если судно, находящееся в т. 1, дополнительным малым кренящим моментом наклонить влево (т.1¢) и отпустить, то в т. 1¢ момент восстанавливающий будет больше кренящего момента Мв > Мкр и судно вернется в т. 1; если судно из т. 1 отклонить вправо в т. 1², то Мкр > Мв и судно снова вернется в т. 1; таким образом, т. 1 является точкой устойчивого равновесия, а участок ДСО от 0 до qm – ветвью устойчивого равновесия. Если судно, находящееся в т. 2 наклонить вправо (т.2¢) и отпустить, то в т. 2¢ момент восстанавливающий будет больше кренящего момента Мв > Мкр и судно вернется в т. 1; если судно из т. 2 отклонить влево в т. 2², то Мкр > Мв и судно опрокинется; таким образом, т. 2 является точкой неустойчивого равновесия, а участок ДСО от qm до qv – ветвью неустойчивого равновесия. Соответственно этому, угол максимума qm делит диаграмму на зоны устойчивого и неустойчивого равновесия и показывает максимальное значение безопасного крена, поскольку для любого значения угла крена q > qm случайное воздействие может привести к опрокидыванию судна.
Угол заката ДСО qv показывает максимальное значение угла крена, до которого диаграмма соответствует положительным значениям восстанавливающего момента. Если у судна угол заливания (угол крена qf, при котором опасные отверстия, через которые забортная вода может поступить внутрь непроницаемого корпуса, входят в воду) qf < qv, то ДСО заканчивается углом заливания.
3.4.2 Начальная метацентрическая высота на ДСО
Рассмотрим Дсо в районе точки 0.
При малых наклонениях судна зависимость плеча статической остойчивости от угла крена определяется из выражения (3.1) как lст = h sinq. Продифференцируем данное выражение по углу крена


 =
= 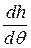 sin q + h cosq. (3.32)
sin q + h cosq. (3.32)
Подставив в выражение (3.32) q = 0, получим
 ½q = 0= h, (3.33)
½q = 0= h, (3.33)
т.е. начальная метацентрическая высота равна производной от диаграммы статической остойчивости в точке 0.
Как известно, производная от кривой в точке равна тангенсу угла наклона касательной к кривой в этой точке (угол a на рис. 3.10); поскольку тангенс угла равен отношению противолежащего катета к прилежащему, то, если прилежащий к углу a катет равен единице (1 рад = 57,3°), то противолежащий катет – тангенсу угла, который, в свою очередь, равен метацентрической высоте. Это свойство метацентрической высоты используется для проверки правильности построения ДСО, а треугольник с катетами, равными одному радиану и метацентрической высоте, называется проверочным – у правильно построенной ДСО начальный участок совпадает с гипотенузой проверочного треугольника.
Проверочный треугольник позволяет также выделить на ДСО участок, соответствующий начальной остойчивости .
Участок ДСО, совпадающий с касательной к диаграмме в точке 0 соответствует начальной остойчивости и описывается линейной зависимостью плеча статической остойчивости от угла крена lст = hq/57,3°, а остальная часть диаграммы соответствует остойчивости при больших наклонениях и описывается выражением lст = lф – lв. Величина lф определяется через координаты ЦВ наклоненного судна, значения которых аналитически не выражаются, поэтому задачи остойчивости при больших наклонениях решаются графически при помощи ДСО.
3.4.3 Построение диаграммы статической остойчивости
Как указывалось выше, перед каждым рейсом на судне производится расчет водоизмещения и координат ЦТ судна на отход и на приход. Завершается этот расчет построением диаграмм статической остойчивости на отход и приход. В зависимости от материалов, имеющихся в Информации об остойчивости, применяется два метода построения ДСО – графоаналитический и графический.
Графоаналитический метод построения основан на использовании пантокарен – интерполяционных кривых плеча формы, показанных на рис. 3.12.
Пантокарены представляют собой кривые зависимости плеча формы lф от водоизмещения судна D для значений угла крена, кратного 5° или 10°. Шкала D включает все возможные значения водоизмещения судна. На поле графика обычно указывается формула, по которой рассчитываются плечи ДСО - lст = lф – lв (3.30) или lст = lф* – lв* (3.31),
где lв = (zg – zc ) sinq; lв* = zg sinq.
Расчет выполняется в табличной форме по образцу таблицы 3.1.
В Информации об остойчивости вместо диаграммы пантокарен может быть приведена таблица зависимости плеч формы от водоизмещения для различных значений угла крена.





 | |||
 | |||
Рис. 3.11. Кривые плеча формы
Таблица 3.1 - Расчет плеч диаграммы статической остойчивости
lст = lф – а sinq
| D= zg = zc= a = zg - zc = | ||||||||
| q, град | ||||||||
| sinq | 0,000 | 0,174 | 0,342 | 0,500 | 0,643 | 0,766 | 0,866 | 0,940 |
| lф | ||||||||
| a sinq | ||||||||
| lст |
Графический способ построения ДСО основан на использовании универсальной диаграммы статической остойчивости, показанной на рис. 3.13.
Универсальная диаграмма статической остойчивости имеет две вертикальных оси: левая – ось плеч статической остойчивости и правая – ось аппликат ЦТ судна (направлена верх) или метацентрических высот (направлена вниз).
На поле диаграммы нанесены кривые плеча формы (из формулы 3.31) для различных значений водоизмещения судна. Для нахождения плеч ДСО на универсальной диаграмме на правой оси откладывают значение аппликаты ЦТ судна или МЦВ; из полученной точки (на рисунке – zg зад) проводят прямую до точки 0 оси углов; поскольку значения углов крена на оси абсцисс диаграммы нанесены на расстояниях от т. 0, пропорциональных синусу соответствующих углов (если расстояние от 0 до 90° принять равным l, то расстояние от 0 до q на оси абсцисс равно l sinq ), эта прямая будет представлять собой плечо веса (zg sinq); кривая плеча формы для заданного водоизмещения D зад проводится методом графического интерполирования между кривыми, соответствующими ближайшим большему и меньшему водоизмещению; искомые плечи ДСО равны длинам отрезков между построенными кривой и прямой (на рисунке – выделенные отрезки).
 |  |










Рис. 3.13. Универсальная ДСО
3.4.4 Практическое использование ДСО
3.4.4.1 Поперечное перемещение (смещение) груза
Кренящий момент, возникающий от смещения груза, пропорционален косинусу угла крена (см. «Перенос малого груза») Мкр = Рlу сosq, где Р – масса сместившегося груза, lу - поперечное смещение ЦТ груза. Подставляя в выражение кренящего момента значения угла крена, получаем точки кривой, которые наносим на ДСО (рис. 3.14). Точка пересечения построенной кривой кренящего момента с кривой восстанавливающего момента на диаграмме определяет величину угла крена qст от смещения груза.
Используя указанный метод, можно определить максимальная масса сместившегося груза Рпр, не приводящее к опрокидыванию судна и предельный угол крена qпр от смещения груза. Для этого необходимо подобрать косинусоиду, касательную к ДСО. Точка касания кривых определяет угол qпр, а коэффициент косинусоиды - Рпр.
Аналогичный подход используется при расчете кренгования судна – наклонения для производства работ на обшивке погруженного участка корпуса судна. Кренящий момент создается перемещением жидких запасов в бортовые цистерны или приемом жидкого балласта.










 |  |
Рис. 3.14
3.4.4.2 Спрямление судна с несимметричной загрузкой
При несимметричной загрузке ЦТ судна не будет находиться в ДП и, соответственно, судно будет иметь статический крен qст . Диаграмма, соответствующая такому случаю загрузки, представлена на рис. 3.15.
Для спрямления судна необходимо создать кренящий момент Мкр, в представленном случае – на левый борт, равный
Мкр = Dyg,
где D - водоизмещение судна; yg - ордината ЦТ судна с несимметричной загрузкой.
Дата добавления: 2014-12-29; просмотров: 950;
