Рейс дальностью 5000 миль 2 страница

Рис. 3.2.Схема продольного наклонения

Если в выражении (3.3) принять дифферент равным одному метру D_f = 1,0 м, то получим выражение момента, дифферентующего на 1 метр

М_1М = . (3.4.)

Если при расчете координат ЦТ судна получено x_g ≠ x_с , то судно будет иметь дифферент, создаваемый продольным моментом сил тяжести и поддержания, равным D(x_g - x_с). Величина дифферента определяется выражением

D_f = .

Осадки носом и кормой определяются по формулам

d_н = d + ( 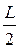- x_f ) ; d_к = d - ( 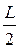+ x_f ) ,

где d – осадка по грузовому размеру.

3.1.2 Расчет метацентрических радиусов

Рассмотрим равнообъемное наклонение плавающего тела произвольной формы (рис. 3.3). Тело имеет погруженный объем V, площадь ватерлинии S, ЦТ площади ватерлинии находится в точке F, ось ординат 0Y лежит в плоскости ВЛ. При бесконечно малом наклонении тела на угол dj центр величины тела точка С смещается в сторону наклонения по дуге окружности радиуса r, центр этой окружности находится в точке m.

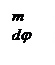
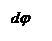
Рис. 3.3. Схема наклонения тела произвольной формы

Пусть ВЛ – начальная ватерлиния плавающего тела, соответствующая его прямому положению, а В₁Л₁ – близкая к ней равнообъемная ватерлиния после наклонения тела на бесконечно малый угол dj. Согласно теореме Эйлера ось рассматриваемого равнообъемного наклонения проходит через точку F – ЦТ площади ватерлинии ВЛ (по нормали к плоскости чертежа). В результате входа в воду клина FЛ₁Л и выхода из воды равновеликого ему клина FВ₁В центр величины переместится из точки С в точку С₁ с ординатой dy_c. Статический момент погруженного объема тела изменится на величину dM_V = Vdy_c. Поскольку угол dj бесконечно малый, dy_c можно считать равной дуге СС₁, тогда dy_c = rdj, а dM_V = Vrdj. Изменение статического момента погруженного объема тела равно статическому моменту объема, вызвавшему это изменение – объема тела, заключенного между ватерлиниями ВЛ и В₁Л₁.

Для определения последнего выделим элементарный объем, представляющий собой призму с основанием dS и вертикальными образующими. Объем призмы равен dS(y – y_f)dj, а статический момент объема - dSy(y – y_f)dj. Проинтегрировав полученный элементарный статический момент по площади ватерлинии S, получим искомое значение dM_V

Vr dj = dj = dj [ - y_f ]. (3.5)

В полученном выражении = I_x – момент инерции площади ватерлинии относительно ее продольной оси 0х; = y_f S. Следовательно, выражение (3.5) принимает вид

Vr = I_x - y_f S = I_F , (3.6)

где I_F – момент инерции площади ватерлинии относительно оси наклонения.

В итоге получаем выражение для начального метацентрического радиуса

r = 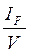(3.7)

Перейдя от плавающего тела произвольной формы к судну, имеющему строгую ориентацию ватерлинии относительно осей 0х и 0у, наклонениям судна относительно главных центральных осей ватерлинии будут соответствовать два главных метацентра m и M и два главных метацентрических радиуса r и R, один из которых будет наименьшим, а другой – наибольшим. В частном случае, когда судно сидит прямо и на ровный киль, проекция на ОП главной продольной оси совпадает с осью 0х, а проекция главной поперечной оси 0y_f параллельна оси 0у. Соответственно этому, выражения для поперечного r и продольного R метацентрических радиусов имеют вид

r = ; R = 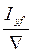, (3.8)

где I_x – момент инерции площади ватерлинии относительно главной продольной оси; I_yf – момент инерции площади ватерлинии относительно главной поперечной оси (оси, параллельной 0у, проходящей через ЦТ площади ватерлинии точку F).

Моменты инерции площади плоской фигуры, имеющей размеры l вдоль оси 0х и b вдоль оси 0у, определяются выражением

i_x = k_x lb³; i_y = k_y l³b, (3.9)

где k_x и k_y– коэффициенты, зависящие от формы фигуры; для прямоугольника k_x = k_y =1/12.

Для судна выражения (3.9) имеют вид

I_x = k_x LB³; I_yf = k_y L³B. (3.10)

Выражения (3.10) позволяют оценить соотношение между продольным и поперечным метацентрическим радиусом

R/r = (k_yL³B /Ñ)/ (k_xLB³/Ñ) = k₁(L/B)², (3.11) где k₁ = k_y/k_x – коэффициент, по величине близкий к 1.

При отношении длины к ширине промыслового судна 5...7 отношение метацентрических радиусов равно 25...50.

Выразим метацентрические высоты через метацентрические радиусы

h = r – (z_g – z_c); H = R – (z_g – z_c).

Поскольку поперечная МЦВ величина малая (обычно 0,2...1,0 м), то возвышение ЦТ судна над ЦВ близко по величине к поперечному метацентрическому радиусу и, следовательно, продольные метацентрическая высота и радиус близкие величины.

Выражение (3.10) позволяет также оценить влияние главных размерений судна на его начальную остойчивость. Поскольку МЦВ отличается от МЦ радиуса на постоянную для данной загрузки величину, то последний также может быть использован в качестве показателя начальной остойчивости. Если подставить в выражение МЦ радиусов Ñ = С_ВLBd, то получим

r = I_x/Ñ = k_xLB³/С_ВLBd = k_rB²/d; R = I_yf/Ñ = k_yL³B/С_ВLBd = k_RL²/d, где k_r = k_x/С_В, k_R= k_y/С_В – коэффициенты, зависящие от формы корпуса судна.

Таким образом, поперечный МЦ радиус прямо пропорционален квадрату ширины судна, а продольный – квадрату длины судна.

Полученные выводы позволяют оценить влияние формы корпуса судна на изменение остойчивости при изменении дифферента.

На рис. 3.4. показан корпус судна, на котором изображены шпангоуты в кормовой части, в районе миделя и в носовой части. Подобная форма корпуса характерна для большинства транспортных судов. Ватерлиния ВЛ соответствует положению судна на ровный киль, В₁ Л₁ – дифференту на нос и В₂Л₂ – дифференту на корму. На нижнем рисунке показаны соответствующие формы ватерлинии. Из рисунка следует, что при дифференте на нос ватерлиния становится шире, а при дифференте на корму – уже. Соответственно, дифферент на нос увеличивает остойчивость, а на корму – уменьшает. Для новых судов в судовой документации z_m дается с учетом дифферента.

Рис. 3.4. Изменение формы ватерлинии

3.2 Некоторые практические расчеты остойчивости

Изложенная выше теория начальной остойчивости позволяет решать большой объем практических задач, возникающих в процессе эксплуатации судна.

3.2.1 Перемещение груза

Пусть на судне водоизмещением D тонн с координатами ЦТ x_g и у_g сидящем прямо и на ровный киль со средней осадкой d_ср груз массой Р перемещается из точки А(x₁; y₁; z₁) в точку В(x₂; y₂; z₂).

Чтобы найти изменение посадки и остойчивости судна от произвольного перемещения груза, рассмотрим раздельно вертикальное, горизонтальное поперечное и горизонтальное продольное перемещения.

Вертикальное перемещение из точки А(x₁; y₁; z₁) в точку А₁(x₁; y₁; z₂) не создает кренящий или дифферентующий момент, а приводит только к изменению координат ЦТ судна, поэтому посадка судна не изменится, а изменится только остойчивость, выражаемая метацентрическими высотами. Поскольку h = z_m – z_g и H = z_М – z_g, при неизменных аппликатах метацентров изменения метацентрических высот будет равно изменению аппликаты ЦТ судна d h = d H = - d z_g. Для определения dz_g составим уравнение статических моментов – изменение статического момента водоизмещения равно статическому моменту, вызвавшего это изменение Ddz_g = Р(z₂- z₁), откуда получаем dz_g = Р(z₂- z₁)/D. В итоге

d h = d H = - Р(z₂ - z₁)/D. (3.12)

Из полученного выражения следует, что перемещение груза вверх (z₂ > z₁) уменьшает остойчивость, а вниз (z₂ < z₁) – увеличивает.

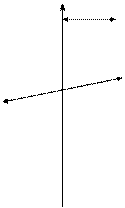
Горизонтальное поперечное перемещение из точки А₁(x₁; y₁; z₂) в точку А₂(x₁; y₂; z₂). При поперечном перемещении груза возникает кренящий момент М_кр, вызывающий наклонение судна на угол q, уравновешиваемый восстанавливающим моментом М_вq = М_кр. Из рис. 3.5 видно, что М_кр = Р(y₂ - y₁) сosq. Используя для определения восстанавливающего момента выражение 3.1, получим

D h sinq = Р(y₂- y₁) сosq.

В итоге, угол крена определяется выражением

q° = arctg . (3.13)

С учетом (3.1.1) это выражение имеет вид

q° = . (3.13.1)

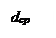
Горизонтальное продольное перемещение из точки А₂(x₁; y₂; z₂) в точку В(x₂; y₂; z₂) показано на рис. 3.6. При продольном перемещении груза возникает дифферентующий момент М_диф = Р(х₂- х₁). Используя (3.4.1), получим

D_f = . (3.14)

Осадки носом и кормой находятся по формулам

d_н = d_ср + ( 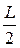- x_f) ;(3.15)

d_к = d_ср - ( 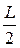+ x_f) ,(3.16)

где x_f – абсцисса ЦТ площади ватерлинии – определяется по гидростатическим кривым.

3.2.2 Прием/снятие малого груза

Малым называется груз, прием или снятие которого существенно не изменяет площадь и форму действующей ватерлинии. В практических расчетах для судна обычных обводов масса малого груза не превышает 5…10 % от водоизмещения судна.

Рассмотрим, как влияет на посадку и остойчивость судна прием малого груза.

Пусть на судно водоизмещением D с координатами ЦТ (x_g, y_g, z_g) и начальной МЦВ h, параметрами посадки d_ср и q = Y = 0, принимается малый груз массой Р в точку (x, y, z). Необходимо определить, какими будут в результате приема груза значения остойчивости h₁ и посадки d_ср1, d_н1, d_к1, D_f1, q₁.

		Y

Рис. 3.5. Поперечное перемещение груза

Р

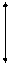
Рис. 3.6. Продольное перемещение груза

Поставленную задачу будем решать в два приема: вначале примем груз в такую точку, чтобы крен и дифферент судна не изменились, и определим, как изменится средняя осадка и остойчивость, а затем известными методами рассчитаем изменение посадки при перемещении груза в заданную точку.

Крен и дифферент судна не изменятся, если ЦТ принятого груза будет находиться на одной вертикали с ЦТ объема, добавленного к погруженному объему судна за счет приема груза Р. Если крен и дифферент судна при приеме груза не изменяются, то новая ватерлиния судна будет параллельна исходной ватерлинии, а ЦТ добавленного объема будет находиться на одной вертикали с ЦТ площади ватерлинии.

Таким образом, считаем, что вначале груз принимается в точку с координатами (x_f, 0, z). Для определения изменения средней осадки запишем уравнение плавучести для судна с принятым грузом

D₁ = gÑ₁,

где D₁ = D + Р; Ñ₁ = Ñ + v; v = Р/g - приращение объемного водоизмещения от приема груза.

Поскольку по определению, при приеме малого груза форма и площадь действующей ватерлинии не изменяется, то приращение объемного водоизмещения v имеет форму прямой призмы, в основании которой лежит ватерлиния, а высота равна приращению средней осадки dd. Таким образом, v = Sd d, Р = g Sd d. Если в полученную формулу подставить значение d d = 1 см = 0,01 м, получим выражение, определяющее q – число тонн на сантиметр осадки

q = 0,01g S, (3.17)

где S – площадь действующей ватерлинии.

Искомая величина изменения средней осадки от приема малого груз Р будет равна d d = Р/gS (м) = Р/(100q), а новая средняя осадка d_ср1 = d_ср + dd.

Для определения изменения остойчивости запишем выражение метацентрической высоты судна, принявшего груз, через метацентрический радиус

h₁ = r₁ – z_g1+ z_c1,

где h₁ = h + d h, r₁ = r + d r, z_g1 = z_g+ d z_g, z_c1= z_c + d z_c;

d h = d r - d z_g + d z_c. (3.18)

Таким образом, используя выражение 3.16, найдем изменение МЦВ d h через приращения соответствующих параметров.

Используя выражение 3.8, запишем d r = r₁ - r = I_x1 /Ñ₁ - I_x /Ñ. Поскольку при приеме малого груза площадь и форма ватерлинии не изменяется I_x1= I_x, а Ñ₁ = Ñ + v. Тогда dr = I_x(1/(Ñ + v) - 1/Ñ) = - (I_x/Ñ)(v/(Ñ + v)) = - rv/(Ñ + v). Умножив числитель и знаменатель полученного выражения на плотность забортной воды g, получим

d r = - rР/(D + Р). (3.19)

Приращение аппликаты ЦТ судна d z_g найдем из уравнения статических моментов (относительно нового ЦТ судна G₁) dz_g(D + P) = (z – z_g)P, откуда

d z_g = (z – z_g)Р/(D + P). (3.20)

Приращение аппликаты ЦВ судна d z_с найдем из уравнения статических моментов объема (относительно нового ЦВ судна С₁) d z_с(Ñ + v) = vl_v, где l_v - плечо объема v. Из рис. 3.7 видно, что l_v = d + d d/2 - z_с; d z_с(Ñ + v) = v(d + d d/2 - z_с); d z_с = (d + d d/2 - z_с)v/ (Ñ + v). Умножив числитель и знаменатель полученного выражения на r, получим

d z_с = (d + d d/2 - z_с)Р/(D + P). (3.21)

Z

Рис. 3.7.

Подставив в (3.18) выражения (3.19 – 3.20), получим

d h = (-r + z_g – z + d + d d/2 – z_c).

Поскольку – r + z_g – z_c = – h, получим

d h = (d + d d/2 – h – z)Р/(D + Р), (3.22) или с учетом (3.17)

d h = (d + d d/(200q) – h – z)Р/(D + Р), (3.23)

Из выражения (3.22) следует, что при приеме малого груза Р остойчивость не изменится (d h = 0), если (d + d d/2 – h – z) = 0 или z = d + d d/2 – h. Последнее выражение является уравнением горизонтальной плоскости, называемой нейтральной плоскостью. Если аппликата ЦТ принимаемого груза оказывается в нейтральной плоскости, то остойчивость судна не изменяется; если груз принимается выше нейтральной плоскости, то остойчивость ухудшается, если ниже – улучшается. Для судна с небольшой МЦВ нейтральная плоскость близка к ватерлинии.

При снятии груза Р и d d меняют знак и выражение (3.22) для приема/снятия груза будет иметь вид

d h = ±(d ± d d/2 – h – z)Р/(D ± Р), (3.24) где верхние знаки соответствуют приему груза, а нижние – снятию.

3.2.3 Подвешенный груз

Рассмотрим подъем груза Р из трюма судовым грузовым устройством. При подрыве груза натяжение шкентеля становится равным весу Р груза. Рис. 3.8 показывает, что при подъеме груза при любом его положении по высоте и любом наклонении судна линия действия силы тяжести, приложенной к грузу, проходит через точку подвеса, что соответствует нахождению ЦТ груза в этой точке. Таким образом, подвешенный груз влияет на остойчивость так же, как при его перемещении в точку подвеса. Если l_п - расстояние между ЦТ груза до подъема и точкой подвеса, то влияние на остойчивость подвешенного груза определится выражением