Методы расчета волноводно-щелевых антенн 7 страница

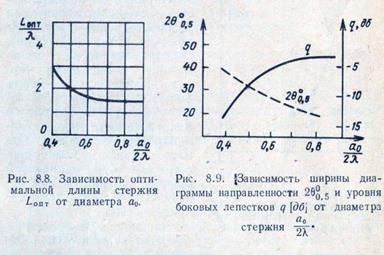
длине L, для которой рассматриваемый метод расчета несправедлив. Зависимость L_oпт от диаметра стержня приведена на рис. 8.8 [Л 3]. Характер зависимости шири­ны диаграммы направленности по уровню половинной мощности 2θ_0,5 и уровня боковых лепестков q от диа­метра стержня при его оптимальной длине приведен на рис. 8.9 [Л 3].

На практике обычно применяются цилиндрические стержни с диаметром a₀=0,3÷0,5λ. Для таких стержней диаграмма направленности антенны определяется мно­жителями F₁(θ) = соsθ и F₃(θ) из рис. 8.6 при c₁=0,5. Однако, как следует из рис. 8.6, ширина основного ле­пестка диаграммы направленности 2θ_0,5 весьма мало зависит от величины c_1. Поэтому при расчете антенны по заданной ширине диаграммы направленности в плоскости Е используется

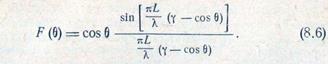
В плоскости Н диаграмма направленности оказыва­ется несколько шире, чем в плоскости Е, из-за отсутст­вия множителя cosθ.

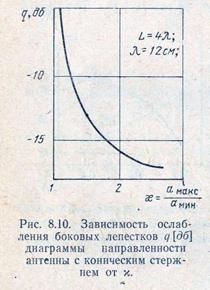
Наряду с цилиндриче­скими стержнями получили распространение конические стержни (см. рис. 8.3,б). Экспериментальные иссле­дования показывают, что они позволяют получить большее ослабление боко­вых лепестков диаграммы направленности, чем ци­линдрические стержни. Од­нако длина конических стержней при одинаковой ширине диаграммы направ­ленности больше, чем ци­линдрических.

На рис. 8.10 приведена зависимость ослабления бо­ковых лепестков диаграммы направленности антенны с коническим стержнем в зави­симости от соотношения его диаметров

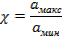
Величина 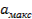для конического стержня определяется из условия (8.5), а величину 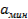следует выбирать из соотношения

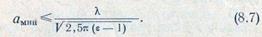
Примером оптимального соотношения диаметров ко­нического полистиролового стержня ε = 2,5 являются 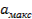= 0,46λ, 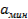=0,31λ.

Расчет диаграммы направленности антенны с кони­ческим стержнем проводится так же, как и для антенны с цилиндрическим стержнем, при условии замены кони­ческого стержня цилиндрическим среднего диаметра.

8.4. К. н. д. и усиление антенны

Коэффициент направленного действия (к. н. д.) ди­электрической стержневой антенны оптимальной длины в осевом направлении вычисляется по формуле

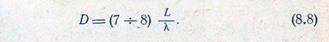
Формула (8.8) характерна для к. н. д. антенны бегущей волны с равномерным непрерывным распределением эле­ментарных диполей по оси антенны, которая является приближенной моделью диэлектрической стержневой антенны.

К. н. д. антенны можно вычислить также по извест­ной ширине диаграммы направленности в плоскости Е и Н.

Коэффициент усиления антенны зависит от величины тепловых потерь в диэлектрическом стержне, которые обычно пренебрежимо малы. Поэтому величину коэффи­циента усиления антенны можно считать равной величи­не к. н. д.

8.5. Возбуждение антенны

Эффективность возбуждения антенны характеризует­ся отношением величины мощности, переносимой волной НЕ₁₁ в стержне к полной мощности, подводимой к антен­не. Эффективность возбуждения во многом зависит от выбора типа возбудителя. Исследования показывают, что наиболее эффективными возбудителями волны типа НЕ₁₁ и в диэлектрическом стержне являются штыревой вибратор и линейная щель, прорезанная в торцевой стенке круглого волновода. Для щели характерна зави­симость эффективности возбуждения от замедления вол­ны в стержне. Этого недостатка лишен штыревой вибра­тор, который обеспечивает более устойчивое возбужде­ние.

При длине волны λ>8 см распространение получила схема возбуждения рис. 8.1, при которой штыревой ви­братор (возбуждения возбуждает диэлектрический стер­жень, заполняющий круглый волновод. Вибратор является продолжением внутреннего проводника ко­аксиальной линии, питающей антенну. Такой возбуди­тель называют волноводно-коаксиальным переходом.

Размеры и положение вибратора в круглом волно­воде выбираются так, чтобы отражения, вызываемые его входным сопротивлением Z_BX в питающей коаксиальной линии в рабочем диапазоне частот, были достаточно ма­лыми. Это обеспечивает минимальные потери в коакси­альной линии, увеличивает ее электрическую прочность и облегчает согласование антенны с генератором или приемником.

Строгий расчет входного сопротивления Z_BX = R_BX + jXвх волноводно-коаксиального перехода весьма сло­жен. При упрощенном методе расчета предполагается, что вибратор возбуждает только основную волну типа Н₁₁ в круглом волноводе, и мощность, излучаемая виб­ратором, приравнивается мощности переносимой этой волной. Это предположение позволяет вычислить сопро­тивление излучения вибратора, составляющего активную часть входного сопротивления R_BX. Расчет проводится по формуле

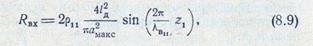
где 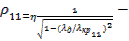волновое сопротивление круглого волновода для волны типа Н₁₁; l_д— действующая длина вибратора;

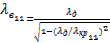—длина волны Н₁₁ в волноводе, заполненном диэлектриком;

λ_д — длина волны рабочего диапазона в диэлектрике; λ_кр11—критическая длина волны Н₁₁, .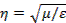

Из выражения (8.9) следует, что величина R_BX может существенно меняться с изменением и достигает макси­мального значения при z₁ = λ_В11 /4.

Реактивная часть входного сопротивления Х_вх волноводно-коаксиального перехода обусловлена возбуждени­ем высших типов волн. Волновод для этих воли является закритическим и они локализованы вблизи вибратора. Теоретический расчет величины Х_вх оказывается доста­точно сложным и на практике она определяется обычно экспериментально. Величина Х_вх, как и величина R_BX, за­висит от положения вибратора в волноводе и может изменяться при его смещении в осевом направлении и в направлении, поперечном оси.

Согласование Z_BX с питающей коаксиальной линией осуществляется подбором величины R_вх из (8.9), равным волновому сопротивлению линии, изменением длины ви­братора при z₁ = λ_B11 /4.

Изменение положения вибратора в круглом волново­де нерационально, так как ведет к значительному иска­жению поля основной волны и появлению интенсивных волн высших типов, ухудшающих диапазонные свойства волноводно-коаксиального перехода. Поэтому для ком­пенсации реактивной составляющей входного сопротив­ления Х_вх в коаксиальной линии используются согласу­ющие элементы в виде шайб, четвертьволновых транс­форматоров или шлейфов с подвижными замыкателями.

Длина стакана L₁ (см. рис. 8.1) от вибратора до раскрыва круглого волновода выбирается так, чтобы выс­шие типы волн не искажали распределение поля основ­ной волны в раскрыве волновода. Ослабление амплитуд ν_mn, ближайших к основной волне высших типов волн, рассчитывается по формуле

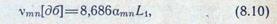
где 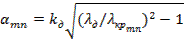— коэффициент затухания

волн высших типов; k_д=2π/λ_д—волновое число в диэлект­рике;

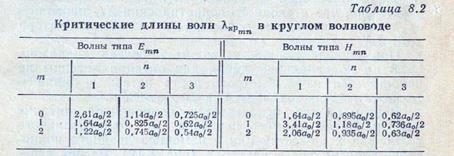
λ_кр —критические длины волн в круглом волноводе

(табл. 8.2).

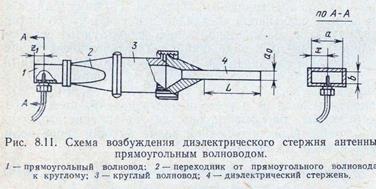
Величина ослабления ν_mn должна быть более 40 дб. Наряду с рассмотренной схемой возбуждения антен­ны (см. рис. 8.1) находит применение схема возбужде­ния, представленная на рис. 8.11. Штыревой вибратор

возбуждает волну Н₁₀ в отрезке прямоугольного волно­вода 1, которая, в свою очередь, через переходник 2 и круглый волновод 3 возбуждает диэлектрический стер­жень 4. Волноводно-коаксиальный переход для прямо­угольного волновода имеет несколько лучшие диапазон­ные свойства и позволяет согласовать Z_BX перехода с питающей коаксиальной линией выбором положения вибратора в прямоугольном волноводе как при его сме­щении по Z, так и по X. Расчет активной части входно­го сопротивления R_вх перехода проводится, как в гл. 6.

Длина отрезков прямоугольного 1, круглого 2 волново­дов и переходника 3 выбирается в соответствии с соот­ношением (8.10).

Величина R_BX выбирается равной волновому сопро­тивлению питающей коаксиальной линии. Компенсация реактивной части входного сопротивления Х_вх проводит­ся экспериментальным подбором смещения вибратора по Z и X.

При уменьшении длины волны рабочего диапазона λ≤8 см коаксиальная линия для питания антенны не используется из-за быстрого роста потерь в линии и технологических трудностей ее изготовления.

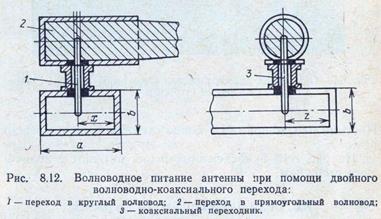
В этом случае используется волноводное питание антенны путем прямого перехода от прямоугольного волновода к круглому или с помощью двойного волноводно-коаксиального перехода (рис. 8.12). Расчет двой­ного перехода проводится на основе выражений для оди­ночных волноводно-коаксиальных переходов 1 и 2. Согла­сование двойного коаксиального перехода с волноводной линией осуществляется выбором положения вибратора в прямоугольном волноводе (z, х). Согласование одиночных волноводно-коаксиальных переходов между собой осу­ществляется размещением согласующих элементов в пе­реходнике 3 и выбором длины последнего.

С целью уменьшения потерь в возбуждающем устрой­стве используется частичное заполнение круглого волно­вода диэлектриком. Форма стержня, вставляемого в круглый волновод, подбирается обычно эксперимен­тально с целью уменьшения отражений, возникающих для основной волны в волноводе.

Частотные свойства входного сопротивления антенны зависят от изменения отражений, возникающих в волноводно-коаксиальном переходе и в диэлектрическом стержне в рабочем диапазоне частот.

Для улучшения диапазонных свойств волноводно- коаксиального перехода, а также его электрической прочности используются вибраторы специального вида [ЛО 1].

Величина коэффициента отражения от конца диэлек­трического стержня поля основной волны оценивается по формуле

|Γ|<|γ-1|,

где γ — коэффициент замедления.

С увеличением диаметра стержня коэффициент |Г| увеличивается. Обычно, для цилиндрических стержней с диаметром а₀<0,5λ и ε = 2,5 величина |Г|≤0,15. Для конических стержней эта величина будет еще меньше.

Поэтому отражениями от конца стержня можно пренеб­речь.

На рис. 8.13 приведен общий вид антенны с кониче­ским стержнем.

8.6. Виды диэлектрических стержней

Помимо антенн со сплошными диэлектрическими стержнями круглого поперечного сечения находят при­менение антенны с диэлектрическими стержнями поло­винного поперечного сечения, помещенными на металли­ческом экране. Поле волны HE₁₁ в таком стержне не искажается, так как оно симметрично относительно пло­скости Н (см. рис. 8.2), а к. н. д. антенны увеличивается вдвое за счет зеркального отображения. В остальном остаются справедливыми все значения, относящиеся к расчету стержней полного поперечного сечения. Такие антенны находят применение в качестве маловыступающих антенн. Кроме того, они весьма удобны для экс­периментального исследования диэлектрических стерж­невых антенн.

Наряду с антеннами, в которых используются сплош­ные диэлектрические стержни, применяются антенны с полыми стержнями пли диэлектрическими трубами. Применение диэлектрических труб предполагает суще­ствование двух границ раз­дела диэлектрик — воздух, что существенно усложняет их изучение. Поэтому в на­стоящее время при проекти­ровании таких антенн осно­вываются лишь на резуль­татах экспериментального исследования.

В отличие от сплошного диэлектрического стержня для диэлектрической трубы характерен сравнительно малый уровень боковых ле­пестков диаграммы направ­ленности (около 10% по полю от уровня основного ле­пестка). Для формирования направленного излучения наиболее удобны тонкостен­ные трубы с толщиной сте­нок 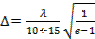Обычно в качестве материа­ла используются текстолиты с ε≈6, которые придают достаточную жесткость кон­струкции антенны.

На рис. 8.14 приведена за­висимость ширины основного

лепестка диаграммы направленности по уровню 6 дб

в зависимости от диаметра трубы [ЛО 13]. Увеличение диаметра трубы приводит к сужению основного лепестка диаграммы при практически неизменном уровне боковых лепестков. Диаметр трубы а следует выбирать равным 1,0÷1,2λ. На рис. 8.15 приведена зависимость величины 2θ_0,5 от длины диэлектрической трубы. Формирование диаграммы направленности диэлектрической трубой про­исходит так же, как в случае антенн бегущей волны с фазовой скоростью, близкой к скорости света. Поэтому диаграмму направленности такой диэлектрической антенны можно рассчитать по формуле

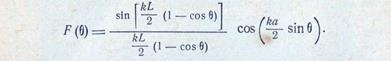
Диаграмма направлен­ности антенны в Е плоско­сти практически не отли­чается от диаграммы в Н плоскости.

Кроме диэлектрических стержней в качестве про­дольных излучателей могут использоваться ферритовые стержни [Л. 1]. Преимущест­вом ферритовых стержней является большое значение диэлектрической проницае­мости (ε=10÷15), что по­зволяет уменьшить размеры излучателя и иметь возмож­ность управления характе­ристиками излучения при подмагничивании стержней. Это свойство, в частности, используется в сканирующих антенных решетках.

8.7. Решетка из диэлектрических стержневых антенн

Решетка из диэлектрических стержневых антенн (рис. 8.16) применяется для сужения диаграммы на­правленности, повышения (коэффициента направленного действия и уменьшения уровня боковых лепестков. Бла­годаря слабой связи между элементами такой решетки упрощается настройка и фазировка этих элементов по сравнению с настройкой решеток, выполненных из эле­ментов других типов.

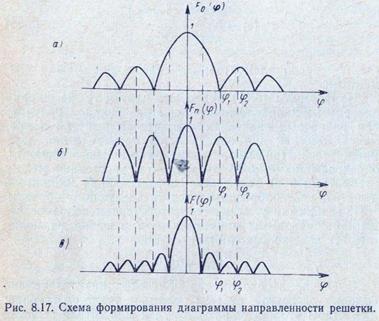
Диаграмма направленности решетки определяется произведением двух множителей

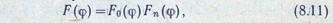
где F₀(φ) —множитель элемента, определяемый прибли­женно формулами (8.1) — (8.3) или (8.6); F_n(φ)—мно­житель решетки.

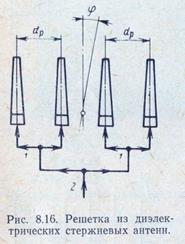
Простейшим случаем является однорядная одноэтаж­ная решетка, позволяющая сузить диаграмму направ­ленности в одной плоскости. Такие диаграммы требуют­ся, например, на корабельных радиолокационных стан­циях.

Множитель решетки в этом случае при синфазном питании элементов в плоскости углов ср определяется формулой

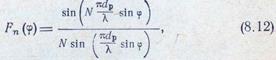
где N— число элементов; d_р — расстояние между эле­ментами.

Из формулы (8.11) видно, что одну и ту же ширину диаграммы направленности решетки можно получить при различных значениях множителей решетки и эле­мента, так как она определяется произведением двух множителей. При выборе размеров отдельного элемента, определяющих множитель элемента, расстояния между элементами и их количества, определяющих множитель решетки, целесообразно поступать следующим образом.

При значении угла φ₀, соответствующем половине за­данной диаграммы направленности решетки по полю, в (8.11) должно выполняться (условие

F (φ₀) =0,707.

В случае необходимости получения низкого уровня боковых лепестков, вторым условием является требова­ние, чтобы угол φ₂ одного из нулей множителя решетки (рис. 8.17,б) совпал с углом максимума первого боко­вого лепестка множителя элемента (рис. 8.17,а). При этом, как видно из рис. 8.17,в уровень боковых лепест­ков значительно уменьшается.

Целесообразно, кроме того, добиваться, чтобы направление φ₁ первого нуля множителя элемента было близким к направлению одного из первых максимумов множителя решетки.

Можно принять, что коэффициент направленного действия решетки в N раз больше, чем коэффициент направленного действия отдельного элемента и опреде­ляется формулой

D≈ND₁

где D₁ — коэффициент направленного действия отдель­ного элемента. Наиболее распространенной схемой питания синфаз­ной решетки является разветвленная схема (см. рис. 8.16). В этой схеме в точках 1 и 2 разветвле­ния фидеров необходимо соблюдать условие согласова­ния. Наиболее широкополосным является согласование без применения трансформаторов сопротивления, когда волновое сопротивление фидера, подводящего питание к точке разветвления, берется вдвое меньше, чем вол­новое сопротивление каждого из двух параллельно под­ключенных к этой точке получающих питание фидеров. Такой способ, однако, мало пригоден при большом чис­ле элементов решетки.

Литература

1. Рудольф Кюн. Микроволновые антенны. Изд-во «Судо­строение», 1967.

2. James I. R. Теоретическое исследование цилиндрических диэлектрических стержневых антенн, Ргос. IiEE (Electronics Record) 1967, april, NT-2, v. .114.

3. Journal Inst. Electr. Comm. Engrs, Japan, 1965 april, v. 48, № 4.

4.

Глава 9

СПИРАЛЬНЫЕ АНТЕННЫ

9.1. Принцип действия

Спиральные антенны относятся к классу антенн бе­гущей волны. Они представляют собой металлическую спираль, питаемую коаксиальной линией. Существуют цилиндрические (рис. 9.1,а), конические (рис. 9.2) и плоские (рис. 9.3) спиральные антенны. В зависимости от числа ветвей спирали, они могут быть однозаходные (одна ветвь), двухзаходные (две ветви) и т. д.

Спиральные антенны формируют диаграмму направ­ленности, состоящую из двух лепестков, расположенных вдоль оси спирали по разные стороны от нее (рис. 9.4).

На практике обычно требуется одностороннее излучение, которое получают, помещая спираль перед экраном или в отражающей полости.

Подробные исследования (см., например, [ЛО 13]) показали, что на излучающей цилиндрической спирали одновременно существует несколько типов волн тока, отличающихся друг от друга амплитудой и числом пе­риодов, укладывающихся вдоль одного витка спирали. Каждая волна распространяется по спирали со своим затуханием и со своей фазовой скоростью. Однако фор­ма диаграммы направленности спирали зависит, в основном, лишь от одной, преобладающей волны, тип

которой определяется соотношением между длиной вит­ка спирали и рабочей длиной волны.

Введем следующие обозначения:

λ — рабочая длина волны в свободном пространстве;

T_q — волна тока в спирали q-го типа; q = 0, 1, 2, ... целое число, указывающее, сколько периодов волны то­ка укладывается вдоль одного витка спирали;

v_q — скорость распространения волны тока T_q по про­воду спирали;

с — скорость света в свободном пространстве;

D — диаметр витка цилиндрической спирали. Известно три режима работы цилиндрической спи­ральной антенны:

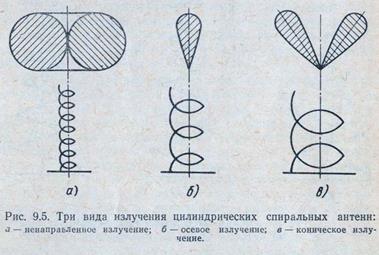
1. Когда длина витка спирали меньше 0,65λ (при этом длина волны λ>5D), на ней преобладает волна Т₀, характеризующаяся изменением фазы тока в пределах 360° на протяжении нескольких витков. Волна Т₀ имеет постоянную по длине спирали амплитуду и фазовую ско­рость Vo = c. Отражение волны Т₀ от конца спирали при­водит к образованию стоячих волн, которые и форми­руют диаграмму направленности антенны. Волна Т₁ име­ет весьма малую амплитуду и в излучении не участвует. Максимальное излучение для этого случая получается в плоскости, перпендикулярной оси спирали (рис. 9.5,а) и в этой плоскости оно не направлено.

2. Если длина витка спирали лежит в пределах от 0,75λ÷1,Зλ, (длина волн соответственно равна λ=4D÷2,2D), на ней преобладает волна T₁, фазовая скорость которой меньше скорости света υ₁≈0,8с. Волна T₁ интен­сивно излучается всеми витками, поэтому в спирали устанавливается бегущая волна тока, формирующая максимум излучения вдоль оси спирали (рис. 9.5,б). Имеющаяся также на спирали волна Т₀ быстро затухает по длине спирали и ее вклад в диаграмму направленно­сти невелик.

Режим осевого излучения является основным, наи­более используемым режимом для работы спиральных антенн, поэтому волна. Т₁ являющаяся преобладающей, когда длина провода витка спирали примерно равна ра­бочей длине волны, называется основной.

3. При длине витка спирали, большей 1,5λ (в этом случае λ<2D), на цилиндрической спирали помимо основного типа волны Т₁ возникают волны Т_2, Т₃ и т. д. Волна Т₁ становится затухающей, в то время как Т₂ имеет постоянную амплитуду и является определяющей в излучении. Максимальное излучение получается в на­правлениях, образующих острый угол относительно оси антенны, и пространственная диаграмма получается в форме конуса (рис. 9.5,в).

Ширина диапазона осевого излучения цилиндриче­ской спирали составляет ±0,Зλ, при этом электрические характеристики изменяются несущественно. Кониче­ская спираль позволяет расширить этот диапазон в два раза, благодаря тому, что область существования основ­ной волны T₁ при изменении частоты автоматически пе­ремещается вдоль спирали.

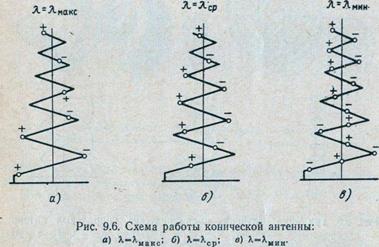
Коническая спираль имеет витки различной длины. Вследствие этого на ней есть группы витков с .преобла­дающими типами волн Т₀, Т₁, Т₂ и т. д. На рис. 9.6,а, б, в схематически показано распределение фаз тока на ко­нической спирали на разных частотах. На этих рисунках видно, что на любой частоте рабочего диапазона на спирали имеется группа витков, на каждом из которых укладывается примерно одна длина волны. Эти виткитна средних частотах диапазона находятся в средней части спирали и работают в режиме, аналогичном ре­жиму излучения цилиндрической спирали, т. е. на них преобладает волна Т₁. На более низких частотах диапа­зона эти витки находятся в области максимальных зна­чений диаметра спирали, на более высоких частотах — в области минимальных значений диаметра.

На витках, диаметр которых меньше требуемого для режима осевого излучения, преобладает волна Т₀, у ко­торой изменение фазы тока в пределах 360^О происхо­дит на протяжении нескольких витков. При этом токи на отдельных витках имеют разные фазы, вследствие чего излучение одних витков ослабляет излучение других витков. В результате участок опирали, на котором суще­ствует волна Т₀, слабо излучает по сравнению с группой витков, возбужденных волной Т₁

На витках, диаметр которых больше требуемого для режима осевого излучения, преобладают волны Т₂, Т₃ и т. д., которые характеризуются тем, что в пределах одного витка укладывается две и более длины волны (фаза тока вдоль одного витка нарастает больше, чем на 720°). Это значит, что на каждом из таких витков имеются противофазные участки, излучение которых взаимоослабляется. Поэтому интенсивность излучения витков, возбужденных волной Т₂ и более высокого по­рядка, также мала по сравнению с излучением группы витков, возбужденных волной Т₁.

Из сказанного следует, что ширина диаграммы на­правленности у конических спиралей определяется не общим числом витков (или полной длиной спирали), а лишь числом витков в группе с волной Т₁ (длиной это­го участка спирали). Излучение остальных витков слабо влияет на форму диаграммы направленности.

Поскольку цилиндрическая спираль сохраняет режим осевого излучения при изменении длины волны от 0,75λ₀ до 1,3λ₀, где λ₀ — длина волны, на которую рассчитыва­ется антенна, то считается, что у конической спирали в группе с волной Т₁ находятся те витки, длина которых составляет от от 0,75λ до 1,3λ,где λ — любая длина волны рабочего диапазона волн конической спиральной ан­тенны.

Хотя вышеприведенные рассуждения, касающиеся работы конической спиралькой антенны, недостаточно строги, они дают простой метод расчета этой антенны,обеспечивающий удовлетворительное совпадение с экс­периментом.

Плоские спиральные антенны выполняются из спира­лей двух видов: равноугольных логарифмических (см. рис. 9,3,а) и архимедовых (см. рис. 9,3,б). Ветви спиралей могут быть либо проводниками, расположен­ными на диэлектрической подложке, либо выполняться в виде щелей в проводящей плоскости. Обычно плоские спирали имеют две ветви и в зависимости от фазовых соотношений в точке возбуждения могут работать в двух режимах: осевом и ненаправленного излучения.

Если две ветви спирали возбуждаются в противофазе, то возникает режим осевого излучения, при котором главный лепесток диаграммы направленности направлен вдоль оси спирали. Для получения противофазного воз­буждения питающий (коаксиальный кабель проклады­вают по одной ветви антенны, электрически соединяя его оболочку с этой ветвью, и замыкают внутренний проводник на вторую ветвь в вершине спирали. Для улучшения симметрии возбуждения на второй ветви также прокладывают коаксиальный кабель, у которого накоротко соединяют центральную жилу с оболочкой.

Режим ненаправленного излучения, при котором ноле максимально в плоскости спирали, имеет место при синфазном возбуждении ее ветвей, когда нейтральный проводник питающего кабеля подключается к точке соединения обеих ветвей спирали, а внешняя оболочка соединяется с экраном.

Объяснение работы плоской спиральной антенны, вы­полненной из архимедовой спирали (см. рис. 9.3,б), ба­зируется на утверждении [Л 1], что ее излучение определяется в основном той полосой на ее поверхности, где токи в смежных элементах спирали почти синфазны. Та­кая полоса имеется как при противофазном, так и при синфазном питании за счет геометрии спирали, т. е. за счет того, что длина каждого последующего витка воз­растает.

При противофазном возбуждении ветвей спирали первая такая полоса (основная) имеет место на витках, периметр которых равен одной длине волны. При син­фазном возбуждении ветвей условие синфазности токов в смежных элементах выполняется на витках, периметр которых приблизительно равен двум длинам волн.

За пределами основной излучающей полосы тока су­ществуют дополнительные полосы, периметры которых кратны периметру основной полосы. Однако экспери­ментальные данные показывают, что эти гармониковые полосы излучают лишь малую часть энергии.

При изменении длины волны основная излучающая полоса автоматически перемещается вдоль спирали, сохраняя постоянство своей электрической длины, вслед­ствие чего диаграмма направленности антенны оказыва­ется частотно независимой.