Методы расчета волноводно-щелевых антенн 1 страница

Существует несколько методов расчета волноводно- щелевых антенн.

Строгие методы расчета связаны со значительными мат ем атич ескими трудностями, поэтому использование их для инженерных расчетов и применения в задачах синтеза не представляется возможным.

При инженерных расчетах обычно используются приближенные методы имеющие ту или иную Степень точности.

С «помощью энергетичеакого метода [ЛО Г, Л О 9], который не учитывает взаимного -влияния щелей по внут­реннему и внешнему .•пространствам, можно приближенно рас считать во л нов о д н о - щ ел ев у ю антенну, В этом методе расчета (предполагается, что фазовый сдвиг между .со­седними 'излучателями по питающему волноводу .равен электрическому расстоянию между ними (2n/X_B)d и фа­зовое распределение в раскрыве антенны линейное.

Однако из-за внешнего и внутреннего взаимного влия­ния щелей в волноводе происходит существенное откло­нение амплитудно-фазового распределения от требуемо­го, а реализуемой ДН от заданной, и. это отличие обус­ловлено ib основном взаимным влиянием щелей по основ­ному типу волны в волповоде [Л 6].

Следующим методом расчета; обеспечивающим при­ближение реализуемого распределения в раскрыве антен­ны к з а данному, по ср авнению с ' энергетическим, явля,- ется метод рекуррентных соотношений |[JI 7], учитываю­щий взаимное влияние щелей по основному типу волны в (питающем волноводе.

Наиболее точный расчет волноводно-щелевои антенны можно выполнить методом последовательных приближе­ний [ЛО 12], который учитывает (внешнее' и внутреннее (по основному и высшим типам волн) взаимодействие щелей в (волноводе. Однако расчет в этом «случае услож-^ няетея.

Рассмотрим два метода расчета вол ново дно-щелевой антенны: метод рекуррентных «соотношений и энергети­ческий.

Метод рекуррентных соотношений [Л. 7]

На рис. 5.8,6 приведена эквивалентная схема вОлно- водно-щелевой антенны с произвольными резонансными щелями (см. рис. 5.1) в виде двухпроводной линии fe шунтирующими пр овод и м о стя м и. Расстояние между соседними проводимостями складывается из расстояния между щелями и отрезков двухпроводной линии, вхо­дящих в эквивалентную схему щелей. Обозначим через ШН u_n-i комплексные амплитуды прямой и обратной волн на входе, а через U._nj и_п комплексные амплитуды прямой и обратной волн ш выходе п-ро 'четырехполюс-

Используя теорию четырехполюсников, можно устано­вить, что действительные А_п-ь Cn-г и мнимые В_пЦ, D_n-1 части комплексных амплитуд прямой и обратной; волн на входе п-го четырехполюсника (U_n-\, u_n-i) сле­дующим образом выражаются через действительные А_п%

С_п и мнимые В_п, Dn части комплексных амплитуд пря­мой и обратной волн (С/_?г>;^:, и_п) на выходе того же четы­рехполюсника:

(n—1)-й и n-й проводимостями на эквивалентной схеме; Д. —электрическое расстояние между щелями вдоль вол-

новода; Д₁^(дг) и Д^^-1*— электрические длины, обусловлен­ные эквивалентной схемой тг-й и (n— 1)-й щелей,

С учетом введенных обозначений мощность, излученная n-й щелью, и фаза излученного щелью ноля Ф_?г соответст­венно равны

где К=0, 1, 2, ...

Используя формулы (5.6)—(5.8), можно проводить расчет волноводно-щёлевых антенн с ^учетом взаимного влияния щелей по основному типу волны в волноводе и без учета их взаимодействия по внешнему пространству и высшим типам волн в волноводе.

При расчете волноводно-щелевых антенн обычно' бы­вают заданными распределения излучаемых мощностей Рп, или амплитуд полей f (z_n) цо щелям и фазы фЦиз­лученных каждой щелью полей. .

Распределение излученных мощностей должно быть нормировано таким образом, чтобы

где мощность на входе антенны принята равной едини­це (Ро= 1 )•; K0P_L/Po — отношение мощности, помещае­мой в нагрузке P_Ly к мощности на входё антенны Рф..

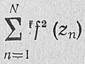
После определения по заданному распределе-

нию по антенне и известному' отноейтельнЪму значению мощности, поглощаемой в нагрузке (обычно;¹, % = 0,05'Я0,1 для получения наибольшего к. -у:, антенны),, находится нормирующий множитель сг, а следовательно, и мощ­ность, излучаемая любой я-й щелью, РЦ [формула (5.10)], 'три условии, что, мощность на входе антенны 'принята равной единице.

Расчет антенны на заданное амплитудное распределе­ние (синтез антенны) .ведется, с" использованием экви­валентной схемц, рис. 5.8, с конца антенны, т. е. с по­следнего :N-ro четырехполюсника. Электрическое рас­стояние,между щелями считается при этом заданным и" постоянным.

Есл<и в нерезоиансной антенне за последней А^-й щелью находится согласованная нагрузка (g_H=1.Un=0),

то в соотношениях (5.6)Bn=Cn=Dn=0 .

Тогда по формуле (5.7) для нормированной проводимо-

Последовательным применением формул (5.6) и (5,13) с предварительной заменой в последней формуле индек­са (N—1) на текущий индекс п, определяются парамет­ры эквивалентной схедш антеннй§||

Величина Д_п== Д^""^ + A J -f- Д{^л)у ; являющаяся элек-

трическим расстоянием между (п — 1)-й и 7г-й проводи- мостями на эквивалентной схеме антенны и входящая в ре­куррентные соотношения (5.6), принимает более простой вид

Дn =Дdn , если в антенне йспользу1бтея продольные щели

в широкой стенке волновода, для которых Д1=-Д2= = 0, рис. 5.8,а [Л 5], а также поперечные щели в широ­кой стенке, у которых Д1=.п/2и Д2=—п/2. В слу­чае более сложных излучателей, например наклонно-сме­щенных щелей в широкой стенке волновода, величины fA^

и Д определяются выражениями, приведенными^ [Л 5].

-Отклонение фазового распределения от линейного в раскрыве антенны, вызванное взаимодействием щелей по основной волне в волноводе, вычисляется по форму­лам

в случае переменнофазно связанных щелей, где Ф_п—- фаза излученного поля л-й щелью {ём. формулу (5.8)].

При вычислениях по формулам (5.14) и (5.14а) в вы­ражении (5.8) для Ф_п число К берется таким, чтобы, раз­ность между величинами, стоящими в правых частях' формул (5.14) и (5.14а),- была наименьшей.

Возможна коррекция фазового распределения в рас­крыве путем изменения расстояния между излучателями d или применением более сложных щелей, но дел ать это нет необходимости, так как в данном методе расчета все равно не учтено внешнее взаимодействие щелей и взаи­модействие по высшим типам волн в волноводе.

Приведенный метод расчета волноводно-щелевых антенн при помощи рекуррентных соотношений (5.6) применим при любом, числе излучателей в антеннах не­резонансного типа при любом амплитудном распределе­нии по раскрыву.

Однако при большом числе излучателей в антенне, т. е. в длинной *) антеене, ее расчет упрощаемся. Дейст­вительно, при большом числе щелей их связь с волново­дом оказывается достаточно слабой и отражения от ще-

*\ Условимся под длинной антенной понимать такую, в которой погонная мощность излучения Мала,

лей пренебрежимо малы. Так как, кроме того, в антенне нерезонансного типа соседние излучатели возбуждаются с небольшим сдвигом по фазе, то на входе антенны по­чти все волны, отраженные от щелей, взаимно компенси­руются и входное сопротивление антенны остается близ­ким к волновому сопротивлению питающего волновода, в котором устанавливается режим, близкий к режиму бе­гущих воли.

В этом случае для расчета параметров антенны мож­но пользоваться энергетическим методом. Укажем при­мерную границу применимости этого метода к антеннам нерезонансного типа.

Проведенные расчеты ;[JI 7] волноводно-щелевых антенн с числом щелей N = 12 на заданное амплитудное распределение энергетическим методом и методом ре­куррентных соотношений показали, что в случае корот­ких антенн (#==12) энергетический метод дает слишком грубое приближение: ошибка в реализуемом распреде­лении мощностей относительно заданного в некоторых излучателях достигает .±-30%. Кроме того, в амплитуд­ное распределение вносится асимметрия.

"Поэтому для приближенного расчету антенны на за­данное амплитудно-фазовое распределение энергетиче­ским методом^ число излучателей следует ориентировочно брать равным: Л/"^: 15, если мощность поглощаемая в со­гласованной нагрузке Шо,05-^-0,1.

При большей мощности, выделяющейся в нагрузке, ччслр N соответственно уменьшается.

Энергетический метод расчета

А н т ен н ы н е-резонансн о г о тип а

Множитель, стоящий в числителе этого выражения (1-х) без^: учета потерь в стенках щелевого волновода,

Учитывая связь [JIO 9] между относительной мощно­стью излучения Р_п, коэффициентом связи щелей с вол­новодом Чп и нормированной проводимостью щели g_n-

можно последовательным пересчетом от последней N-& щели к первой определить сначала относительные мощ­ности излучения Р_п всех щелей по заданному амплитуд­ному распределению и к. п. д. антенны, затем коэффи­циенты связи а_п и, наконец, эквивалентные нормирован­ные проводимости щелей g_n [формула (5.17)]. По извест­ным проводимостям щелей рассчитываются элементы связи, т. е. определяются смещения щелей относительно оси 1в0лновода xl или их угол наклона б (§ 5.2, табл. 5J1), В случае идентичных щелевых излучателей (экспо­ненциальное распределение амплитуд поля по антенне), когда эквивалентные проводимости (или сопротивления) всех щелей равны, для определения последних по задан­ному коэффициенту полезного действия антенны г]_А можно пользоваться формулой (5.17), где

Р е з о н а я с н ы е а н т е h h ы

Резонансная антенна с произвольными резонансными щелями и расстоянием между ними d=X_B/2 (или д?=Я_в), рассчитывается энергетическим методом следующим об­разом.

Если распределение по антенне обозначить, как и ра­нее, через f(z_n) и учесть, что все щели резонансные, то

эквивалентная нормированная; проводимость п-и щели будет равна [ЛО 1]

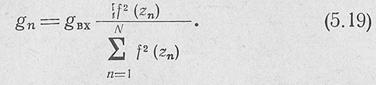
Входящая в формулу (5.19) входная проводимость антенны g_Bx выбирается так, чтобы обеспечить хорошее согласование антенны с -питающим волноводом. Так, ве­личина g_Bx 'может быть выбрана равной единице [ом. ниже § 5.5].

Ант енны ; с согл а со в а н н ы м и щел я: ми

Как указывалось в § 5.3, наряду с простыми щелями применяются и наклонно-смещенные щели на широкой ' стенке волновода, характеризующиеся двумя геометриче­скими параметрами: -смещением 'Xi и. углом поворота Щ с помощью которых можно регулировать ~ независимо амплитуду и фазу поля, излучаемого щелью. Наиболь­ший практический интерес представляхот^соглансованные наклонно-смещенные щели, при применении которых от­сутствует взаимное влияние излучателей по основной волне. Так как отражения от излучателей отсутствуют и в антенне устанавливается режим бегущей волны, расчет антенны на заданное распределение производится энер­гетическим методом по вышеприведенным формулам для нерезонансныхЩнтенн.

Вышеизложенные . методы расчета волноводно-щеле- вьгх антенн со щелями, эквивалентными параллельным проводимостям включенным в линию, эквивалентную волноводу, остаются справедливыми и для щелей, экви­валентных сопротивлениям г_П} которые включены в линию последовательно. Поэтому расчет антенны проводится Аналогично с условием замены в соответствующих вы­ражениях нормированных проводимостей, g_n нормиро­ванными сопротивлениями г_п.

5.5. Согласование щелевой антенны с питающим

волноводом

О согласовании антенны с питающим волноводом обычно судят по величине коэффициента дтражения от входа антенны. В случае нерезонансной антенны с око­нечной согл асованной нагрузкой коэффициент отражения

от входа антенны определяется выражением [ЛО 1]

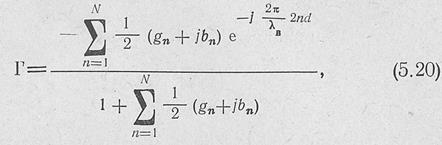
. где g_n+jb_n — полная эквивалентная нормированная проводимость п-й щели,

В , случае идентичных щелевых излучателей, когда проводимости всех щелей одинаковы, это выражение принимает вид ;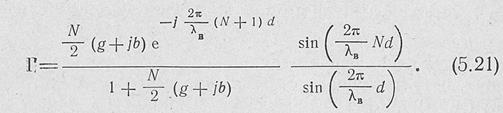

Из формульг (5 21) следует, что коэффициент отра­жения принимает, нулевое значение (к. с. в.= 1) при

Отсюда определяется расстояние, между щелями d так, чтобы во всем рабочем диапазоне изменений Я не получалось резонансного возбуждения антенны и в ДН не появлялись бы главные максимумы высших порядков:

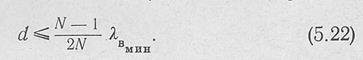
Формула (5:22) получена для частного случая, когда проводимости всех щелей равны. Если проводимости ще­лей в волноводно-щелевой антенне не одинаковы, то при­веденной формулой все же можно пользоваться для ориентировочного определения расстояния между излу­чателями d.

В случае многощелёвой резонансной антенны для обеспечения ее согласования с питающим!; волноводом (к. б. (В.= 1) при любодо амплитудном распределении (по раскрыву часто используют короткозамыкающий пор­шень на ее конце. При расстоянии между излучателями Хв/2 (или Х_в) и расстоянии от центра последней щели до поршня, равном (2/?—1)А,в/4 в случае продольных щёшей

и реяв/г) в случае поперечных (здесь /7=1, 2, .. О/ко­эффициент отражения на входе антенны равен нулю; если сумма проводимостей всех щелей

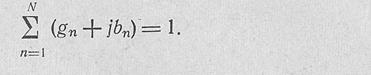
5.6. Влияние изменения частоты на характеристики

антенны

Рассмотрение выражения для коэффициента отраже­ния от входа антенны показывает, что при изменении частоты в формуле (5.20) меняется как величина

— 2nd, так и полная проводимость каждой щели +

Лв

ШЬп.

Расчет и эксперимент показывают*; что при неболь­ших, обычно используемых изменениях частоты, отклоне­ния проводимостей щелей от номинальных значений ма­лы и основное влияние на изменение коэффициента отра­

жения, а следовательно, и в., оказывает изменение электрического расстояния между ними d^J.

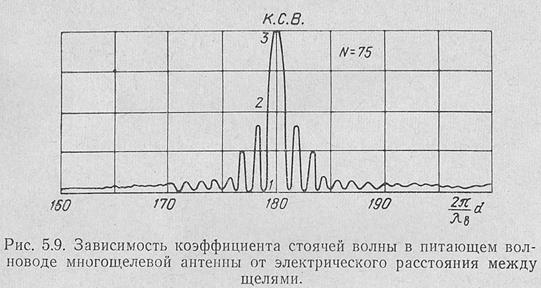
Зависимость к. с. в. многощелевой антенны [JIO 1] от изменения электрического расстояния между излучателя­ми при изменении частоты показана на рис. 5.9.

При выборе расстояния между щелями по формуле (5.22) рабочая полоса антенны лежи#|вне границ «глав­ного лепестка» к. с. в.у определяемых значением к. с. в.—

136 "'== 1и согласование хорошее. Рабочая полоса пропуска- , ния резонансных антенн лежит в области «главного лепестка» к. с. в. (рис! 5.9), что определяет резкое изме­нение коэффициента отражения при изменении частоты.

Изменение чатоты сказывается не только на согласо­вании антенны, но и на излучении. При оценке влияния изменения частоты на излучение: излучающие свойства отдельных элементов; в первом приближении можно счи­тать частотно независимыми i[JI 1), так же как й при рас­смотрении согласования. В этом случае изменение ча­стоты приводит к повороту луча в пространстве [см: гл. 2], что связано с изменением фазового набега вдоль волновода и это отклонение луча может; быть подсчитано по формуле (5.26).

5.7. Направленные свойства волноводно-щелевых

антенн

Для расчета диаграмм направленности многощелевых антенн используют те же методы, что и для многовибра­торных антенн. При этом форма диаграммы направлен­ности определяется амплитудно-фазовым распределе­нием по раскрыву антенны. ⁴

На практике наиболее часто используются следующие виды амплитудных .распределений: равномерное, симме­тричное спадающее относительно центра антенны, экспо­ненциальное. Фазовое распределение чаще всего линей­ное. Случай специальных амплитудных распределений рассмотрен в гл. 4.

Нормированная диаграмма направленности линейной решетки идентичных излучателей может быть записана в виде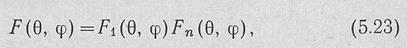

где Fi(0, ф)^Ядиаграмма направленности одного излу­чателя; /чСЭ, ф) —множитель антенны, зависящий от числа щелей в антенне.

Приведем выражения для множителя антенны F_n(0) при различных амплитудных распределениях по антенне. В случае равномерного амплитудного и линейного фазо­вого распределения по длине решетки

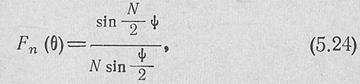
где Ш^^НВЯ—сдвиг по фазе между полями, соз­даваемыми в точке наблюдения соседними излучателями; к == 2я/Я— фазовая постоянная свободного пространства; 0 — угол, отсчитываемый от нормали к линии располо- жения излучателей, рис. 5.10; г|н — разность фаз сосед­них щелей по системе питания; #-эчисло щелей,

В синфазной антенне —0; в нерезонансной антенне с

■ 2тс .

синфазной связью уцелей с полем волновода d; в

Если распределение поля по раскрыву дискретной ли­нейной решетки излучателей э'ксп о;нен ци а л ьн о ё, то

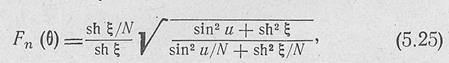
где 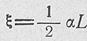— величина, ; характеризующая неравномер­

ность амплитудного распределения по раскрыву; а =-а_Е -(-

+ а_ст — постоянная затухания в неперах/метр, вызванного потерями на излучение и в стенках волновода; в волноводе с малыми потерями а^ а_Е и а ^ а₂;: L WNd — длина ан­тенны; 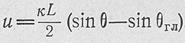обобщенная координата; 0_ГД—

направление главного максимума ДН антенны.

Отклонение главного максимума ДН от нормали к линии расположения излучателей определяется., по формуле

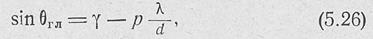
[1] Формула получена Г. А. Евстроповым и Г. К. Фридманом.

где — замедление фазовой скорости в волноводе;

р = 0 для си'нфазно связанных щелей с полем волновода и /? = 0,5 для переменнофазно: связанных щелей.

Для определения постоянной затухания а₂ можно воспользоваться следующим очевидным соотношением:

- 1 у Р₀ ^az 2Nd ^Ш P_L '

В случае антенны .с симметричным относительно центра и "спадающим к краям амплитудным распределением, например косинусоида льны м, р а счет ДН при большом числе излучателей связан с трудоемкими вычислениями [суммы в формулах 2.5 IX, 3.5 IX (ЛО 1)].

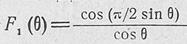
поперечная

Для выполнения расчетов в этом случае можно вос­пользоваться множителем антенны с непрерывным рас­пределением ненаправленных излучателей F_L (0) [Л 8], так как ДН дискретной решетки и непрерывной при

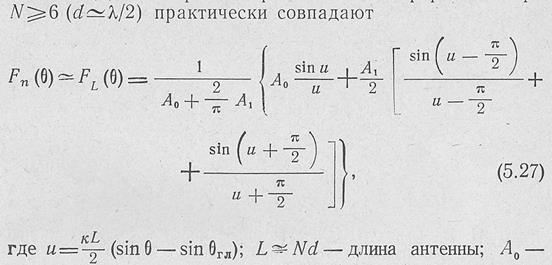
амплитуда поля на краях антенны. При приведении амплитудного распределения по антенне к единице

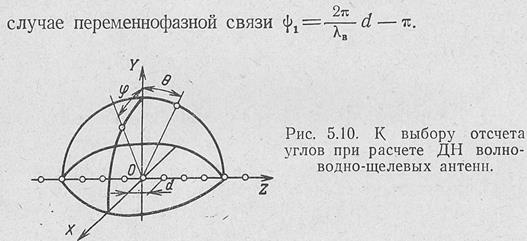
Диаграмму направленности одной/щели F±(0) в плоско­сти YOZ, проходящей через линию расположения излу­чателей (рис. 5.10), можно при инженерных расчетах определять ро формулам ДН щели © бесконечном

экране: продольная щель

F± (б) ==■1, так как длина антенны обычно большая (не­сколько К) и, кроме того, направленные свойства

ШШ ШШИяШШ ННВ . 139

антенны в этой плоскости определяются в основном мно­жителем антенны F_n (Q)-

При определении ДН в поперечной плоскости (пл. YOX рис. 5.10) антенны с продольными щелями в широ­кой стенке волновода следует учитывать, что конечные размеры экрана (поперечного сечения волновода) суще­ственно влияют на форму диаграммы [ЛО 9]: ограничен­ность экрана придает излучению направленность—шоле

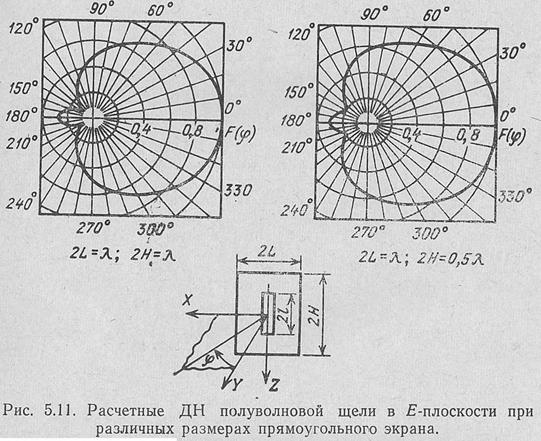
в направлении щрана-уменьшается примерно до (40-:- 50) % относительно значения поля в направлении макси­мума ДН.

Для упрощения нахождения ДН щели в плоскости, нормальной ее продольной оси (плоскость YOX), волно­вод удобно заменить плоской лентой той же ширины [ДО 3]. Топда оказывается, что ери ширине волновода а = (0,7-^-0,8)IX ДН будет близка к любой из диаграмм, изображенных на рис. 5.11.

В случае-поперечных щелей на широкой стенке вол­новода или наклонных в узкой стенке ДН в плоскости YOX можно ориентировочно оценить по формулам ДН щели в бесконечном экране, так как размеры экрана в на-

правлении оси щели мало влияют на ДН как в ^-плоско­сти щели, так и в Я-плоскости [ЛО 9].

В табл. 5:2 приведены формулы для определения ши­рины ДН синфазных щелевых антенн и указаны уровни первых боковых лепестков в децибелах при различных амплитудных распределениях по антеше.

Указанными формулами ширины луча можно вос­пользоваться и в случае нерезонансных антенн* так как расстояние между излучателями в таких антеннах [фор­мула (5.22)] незначительно отличается от синфазного случая и угол отклонения луча от нормали к антенне мал.

В тех специальных случаях, когда требуется значи­тельное отклонение луча от нормали к антенне в форму­лы для ширины луча 20_о,₅ следует вместо длиньь антенны L<^.Nd подставить эффективную длину раскрыва £_Эф — cos 0_rjT.

Коэффициент ^направленного действия (к. н. д .) антенны с переменнофазными щелями в широкой или узкой стенках

волновода при 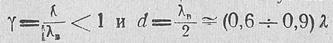рпредё- ляется следующей приближенной формулой:

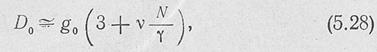
где для продольных щелей в широкой стенке и

vp для наклонных щелей в узкой стенке волновода (при 6^15°).

Входящий в формулу (5.28) коэффициент использо­вания раскрыв a go зависит от амплитудного распределе­ния по антенне: при равномерном распределении go —-1; при экспоненциальном g|§=0,85 и 0,92, если к=Рь/Ро — =5%' или 10%; при косинусоидальном распределении, когда амплитуда (поля «а краях антенны имеет значения Ао$0 или А₀=0,5 щЩ0,81 и 0,965.

По формуле (5.28) можно оценить к. н. д. антенны и при сканировании, если угол отклонения луча 0гл^ ^40°, dfX^Ofi и длина антенны так как из­

менение к. н. д. антенны при сканировании в указанных пределах из-за изменения эффективной длины раскрыва компенсируется тем, что линейная антенна при 0_ГЛ—^90° становится направленной в двух плоскостях, в то время как при 0гл = О° антенна ймела ; направленность в одной плоскости [JT 9].

В отличие от линейной плоская решетка излучателей имеет направленность в обеих главных плоскостях и по­этому ее к. н. д. при сканировании сразу же начинает па­дать за счет уменьшения эффективной апертуры ре­шетки. I

Коэффициент полезного действия (к. п. д.) нерезо- йяансной вошовото-щелевой антенны т)_А может быть подсчитан по формулам (2.8) или (2.11) гл. 2.

Так как в резонансной антенне вместо поглощающей нагрузки обычно устанавливают короткозамыкающий поршень, ее к. п. д. выше, чем нерезонансной антенны тех же размеров. При известных к. п. д. и к. н. д. антенны коэффициент усиления вычисляется по формуле

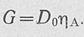
5.8. Возможные схемы построения вол ново дно-щелевых антенн и примеры конструкций

В зависимости от назначения антенны она может быть выполнена в виде линейной и плоской волноводно- щелевой антенны или состоять из набора линейных ще­левых антенн, расположенных по образующим поверхно­сти летательного аппарата (ри.сД 5.12-Ш5.17). Схематич­ное изображение части линейной антенны с наклонными щелями в узкой стенке волновода, используемой в судо­вых радиолокационных устройствах, показано на рис. 5.12. Для ослабления паразитной составляющей по-

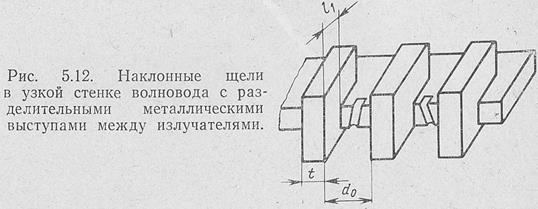
ля излучения такой антенны, поляризованной поперечно волноводу, между соседними щелями установлены раз­делительные металлические выступы [Л 1]. При извест­ном расстоянии ме^кду соседними излучающими щелями с использованием основных положений'о затухании волн