Инерционное (апериодическое) звено
Инерционным (апериодическим) звеном 1 – го порядка называется такое звено, связь между выходом и входом определяется линейным заданным уравнением первого порядка вида
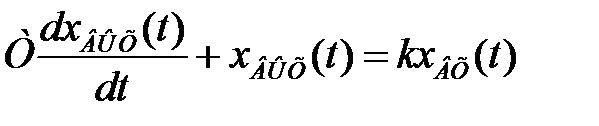 , (2.22)
, (2.22)
где Т – постоянная времени инерционного звена, обусловленная наличием
массы, момента инерции, индуктивности ёмкости и т.д.;
k – коэффициент усиления (или передачи).
При линеаризации уравнений и соответствующем упрощении математического описания примерами инерционных звеньев могут служить многие объекты: генераторы, двигатели, электрические печи, а также исполнительные механизмы, электронные усилители, проходные четырёхполюсники, содержащие индуктивности или ёмкости.
Применяя к (2.22) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
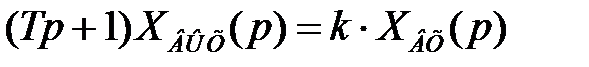 , (2.23)
, (2.23)
Передаточная функция инерционного звена первого порядка на основании (2.23) запишется как
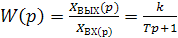 , (2.24)
, (2.24)
Решение уравнений (2.23) или (2.24) может быть представлено в виде
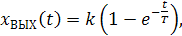 (2.25)
(2.25)
(рисунок 2.9, а).
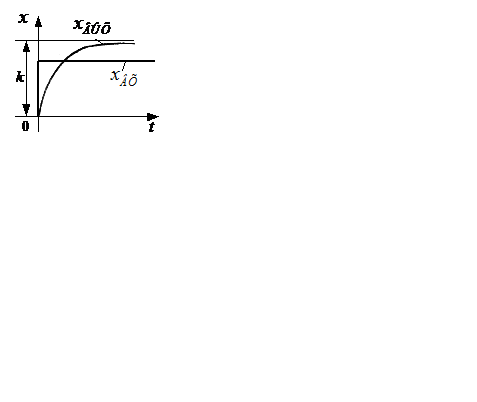 а) б)
а) б)

Рисунок 2.9 – Переходная функция (а) и изображение (б)
инерционного звена
Изображение инерционного звена на структурных схемах показано на рисунке 2.9,б.
Частотная функция звена первого порядка получается путём замены р на jω в выражении (2.24)
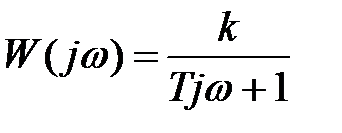 , (2.26)
, (2.26)
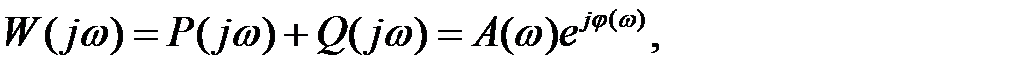 или (2.27)
или (2.27)
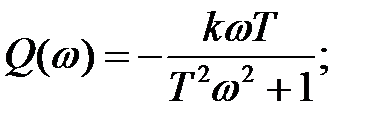
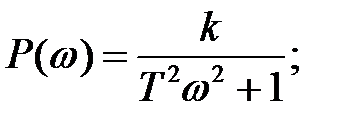 где
где
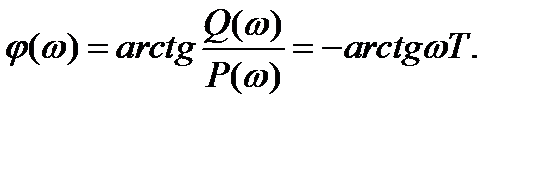
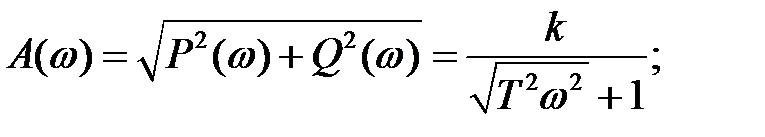 (2.28)
(2.28)
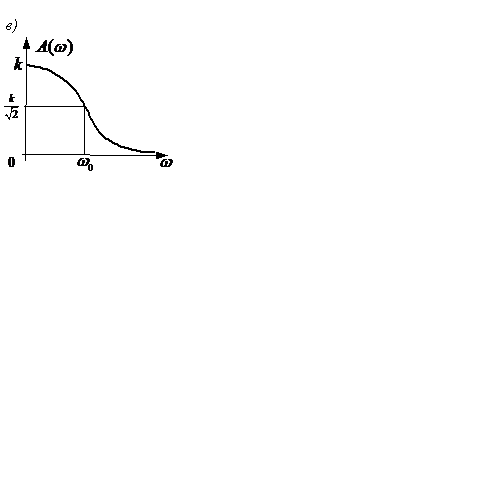 Частотный годограф и частотные характеристики инерционного звена рассчитаны в таблице 2.1 и показаны на рисунке 2.10,а и б,в . Таким образом, АФЧХ инерционного звена представляет собой полуокружность радиуса
Частотный годограф и частотные характеристики инерционного звена рассчитаны в таблице 2.1 и показаны на рисунке 2.10,а и б,в . Таким образом, АФЧХ инерционного звена представляет собой полуокружность радиуса 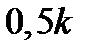 с центром окружности, отстоящим от начала координат на
с центром окружности, отстоящим от начала координат на 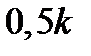 , и при изменении частоты от
, и при изменении частоты от 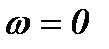 до
до 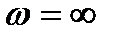 вектор
вектор 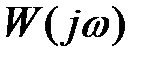 поворачивает на угол, равный
поворачивает на угол, равный 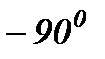 .
.
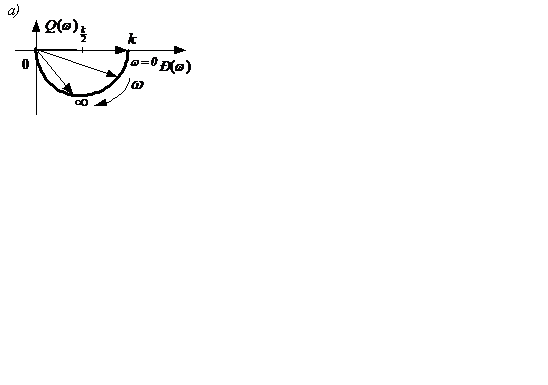
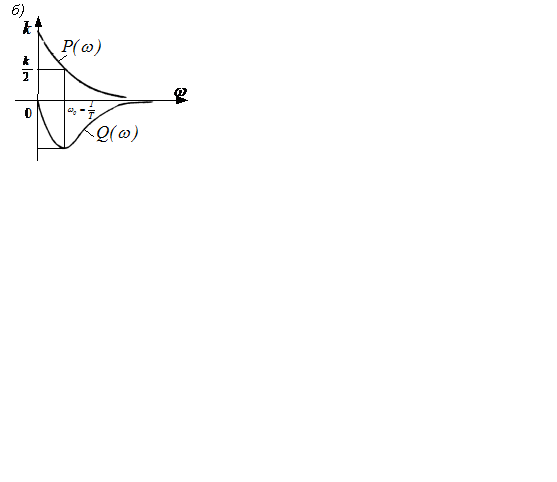
Рисунок 2.10
Логарифмическая амплитудно-фазовая частотная характеристика имеет вид
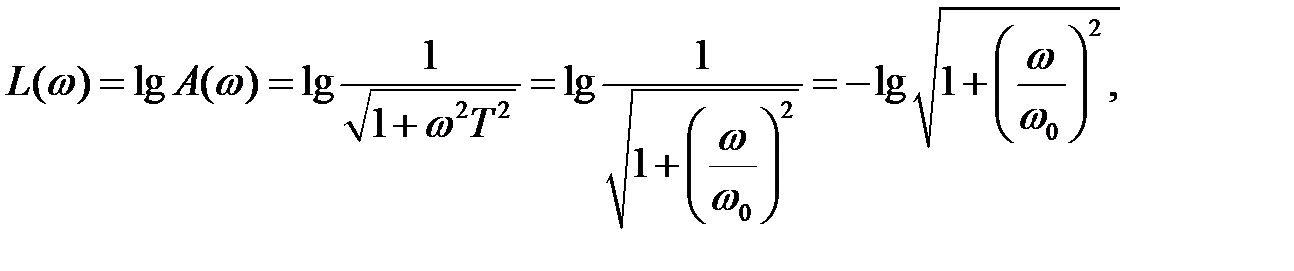
(2.29)
где 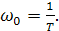
Точное построение L(ω) заключается в последовательном определении значений L(ω) при различных частотах ω (таблица 2.1 и рисунок 2.11). Построение ЛАХ обычно упрощают, заменяя точную L’(ω) асимптотами. Первая асимптота характеризует 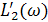 при малых частотах, когда величиной ω2Т2 можно пренебречь, т.е. принимают
при малых частотах, когда величиной ω2Т2 можно пренебречь, т.е. принимают
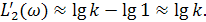 (2.30)
(2.30)
Эта асимптота не зависит от частоты. Вторая асимптота характеризует 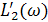 при больших частотах, когда ω2Т2 »1,
при больших частотах, когда ω2Т2 »1,
т.е. принимают
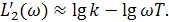 (2.31)
(2.31)
Эта асимптота зависит от частоты. Если принять приращение частоты на одну декаду (ω2=10 ω1), то амплитуда изменится на величину
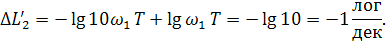
Следовательно, для второй асимптоты известен наклон, характеризующий убывание амплитуды на 1 лог при возрастании частоты на 1дек (она проходит под углом -45° в том масштабе, который дан в п. 1.3). Точка сопряжения обеих асимптот будет удовлетворять равенствам (2.30) и (2.31)
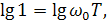
откуда 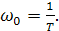
Величина ω0 определяется постоянной времени инерционного звена первого порядка и называется сопрягающей частотой.
Таблица 2.1
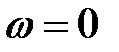
| 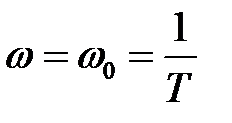
| 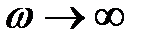
| |
| P(ω) | k | k/2 | |
| Q(ω) | -k/2 | ||
| A(ω) | k | 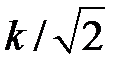
| |
| L(ω) | lg k | 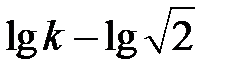
| 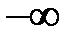
|
| φ(ω) | 0o | -45o | -90o |
На основании изложенного можно сформулировать следующий порядок построения ЛАЧХ инерционного звена первого порядка, имеющего коэффициент усиления k: 1) определяется логарифм амплитуды частотной функции в логах; 2) рассчитывается сопрягающая частота в декадах; 3) через 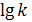 проводится горизонтальная прямая до точки сопрягающей частоты; 4) проводится прямая с наклоном -1
проводится горизонтальная прямая до точки сопрягающей частоты; 4) проводится прямая с наклоном -1  после точки сопрягающей частоты от конца горизонтального участка ЛАЧХ (рисунок 2.11). Максимальное отклонение асимптотической ЛАЧХ L2 от действительной L1 равно 0,15 лог при частоте ω0 и незначительно при других частотах.
после точки сопрягающей частоты от конца горизонтального участка ЛАЧХ (рисунок 2.11). Максимальное отклонение асимптотической ЛАЧХ L2 от действительной L1 равно 0,15 лог при частоте ω0 и незначительно при других частотах.
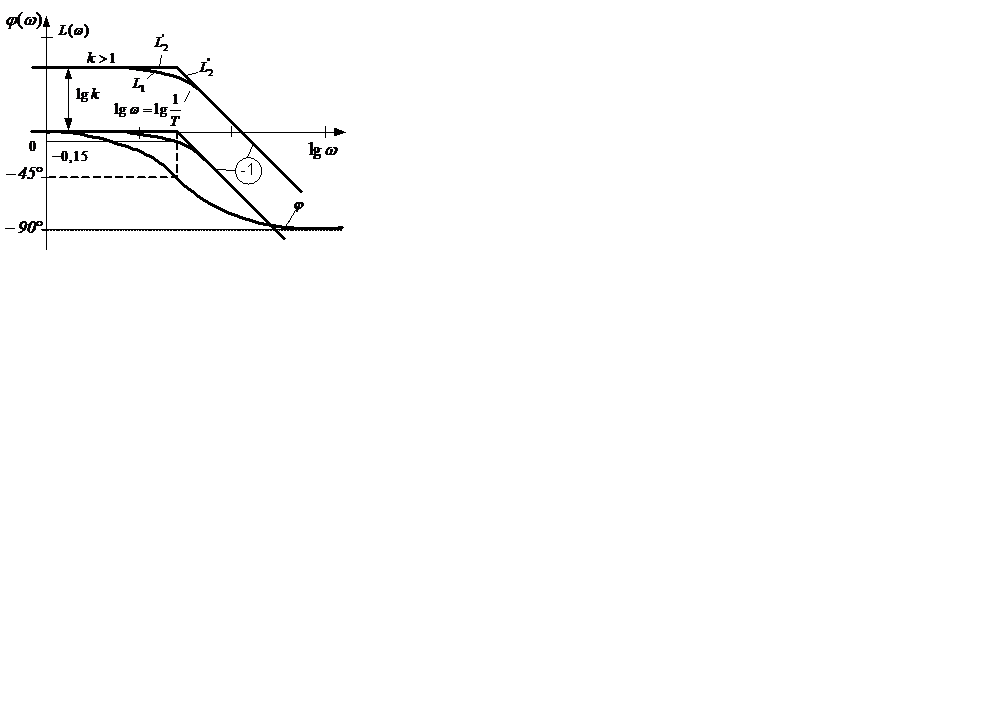
Рисунок 2.11 – ЛАЧХ и ЛФЧХ инерционного звена первого порядка
Логарифмическая фазо-частотная характеристика инерционного звена первого порядка 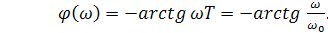
Для сопрягающей частоты фаза
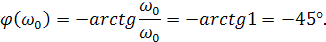
Логарифмическую фазо-частотную характеристику целесообразно строить по шаблонам или по точкам относительно ординаты сопрягающей частоты (таблица 2.1).
Примерами инерционного звена первого порядка являются: пассивные четырёхполюсники, состоящие из сопротивления и индуктивности или из сопротивления и ёмкости; термопара, генераторы постоянного и переменного тока; электрические двигатели (если вход – ток якоря, а выход – угловая скорость) и т.д., если уравнения можно представить в виде (2.22).
Дата добавления: 2014-12-22; просмотров: 1647;
