Реальное дифференцирующее звено первого порядка
Это звено, у которого связь между выходной и входной величиной определяется уравнением вида
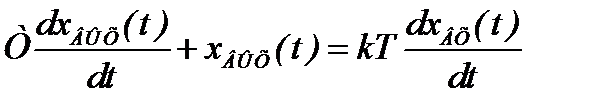, (2.32)
где Т – постоянная времени звена;
k – коэффициент усиления звена.
Такие звенья называются реальными дифференцирующими, или инерционно-дифференцирующими. Реальные дифференцирующие звенья применяются как средство корректирования переходных процессов, например, стабилизирующий трансформатор, дифференцирующие мостовые схемы и другое.
Применяя к (2.32) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
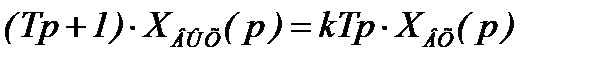. (2.33)
Переходная функция звена
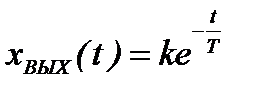. (2.34)
Переходная функция реального дифференцирующего звена, построенная по (2.34) при единичном ступенчатом воздействии, представляет собой экспоненциальную кривую (рисунок 2.12,а).
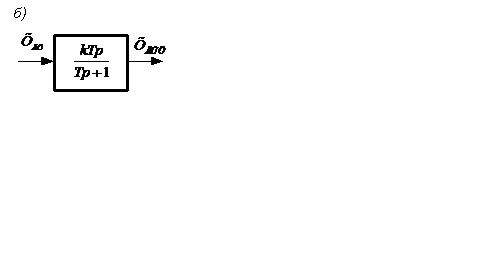
Рисунок 2.12 – Переходная функция (а) и изображение (б)
на структурных схемах реального дифференцирующего звена
Передаточная функция реального дифференцирующего звена на основании (2.33) запишется как
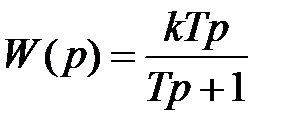. (2.35)
Комплексный коэффициент передачи получается заменой p на jω в выражении (2.35):
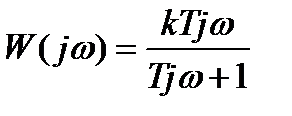, (2.36)
или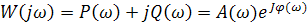 
, (2.37)
где
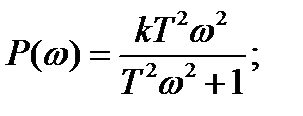
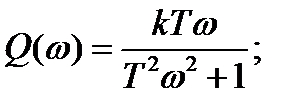(2.38)
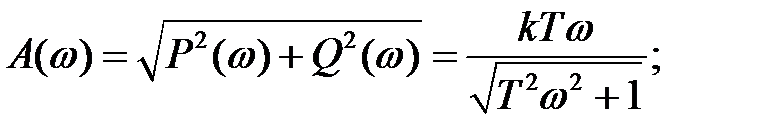
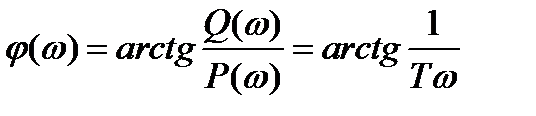. (2.39)
Частотные характеристики показаны на рисунке 2.13, а…в.
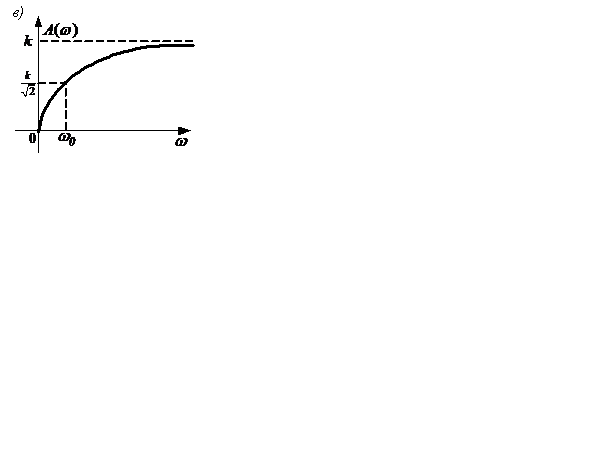
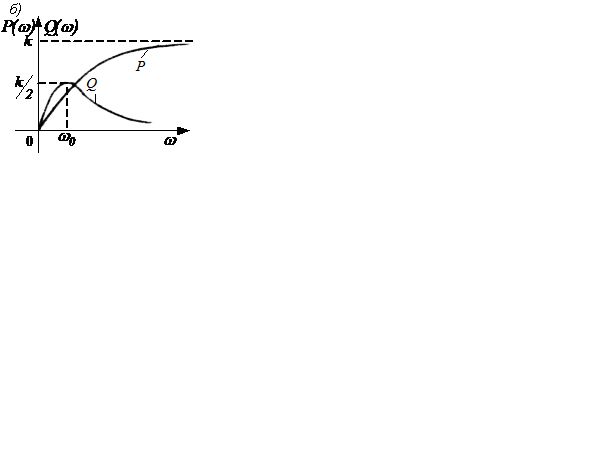
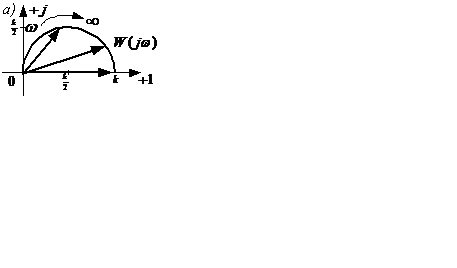
Рисунок 2.13
Логарифмическая амплитудно-частотная характеристика
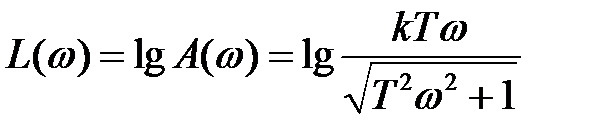(2.40)
рассчитана по формуле (2.40) в таблице, аналогичной инерционному звену первого порядка, и представлена на рисунке 2.14
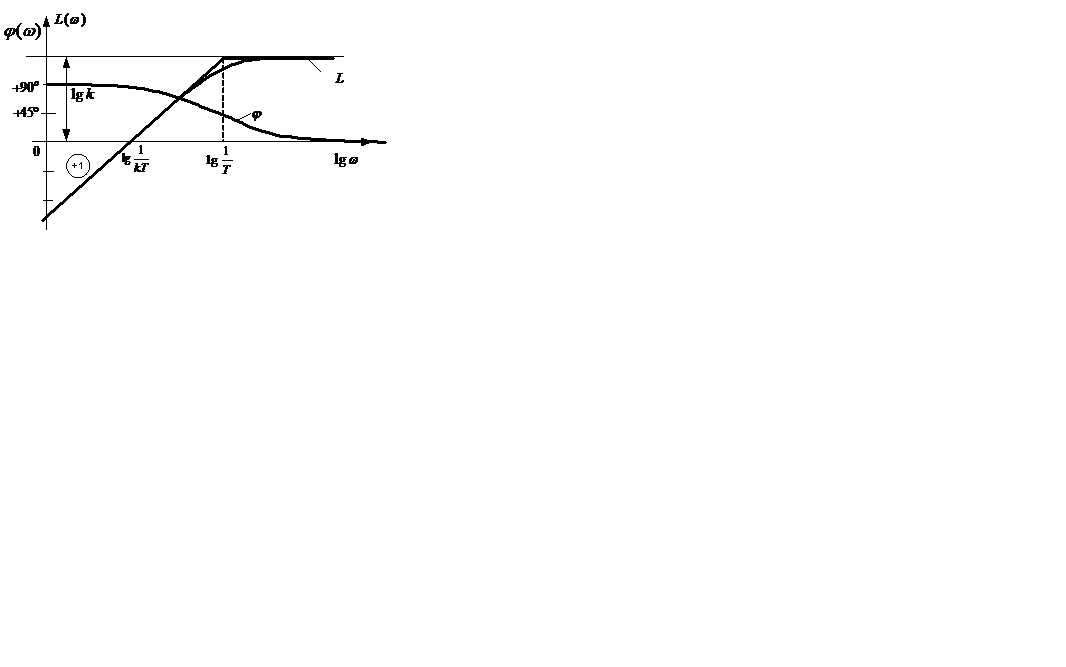
Рисунок 2.14 – ЛАЧХ и ЛФЧХ реального дифференцирующего звена
Асимптотическая характеристика состоит из двух полупрямых
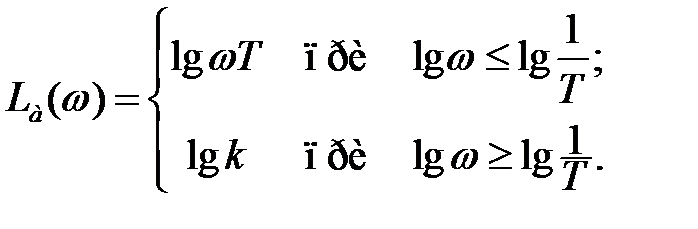
Так же, как и в инерционных звеньях, поправка к асимптотической характеристике имеет вид кривой на рисунке 2.11, но с противоположным знаком.
Логарифмическая фазо-частотная характеристика реального дифференцирующего звена
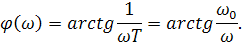
Эта характеристика является характеристикой инерционного звена первого порядка, но приподнятой на 90° вдоль оси φ(ω).
2.1.3 Форсирующее звено 1 – го порядка
Звено, описываемое дифференциальным уравнением
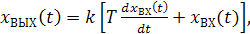(2.41)
называется форсирующим звеном. Такое звено получается в результате соединения пропорционального и дифференцирующего звеньев.
В уравнении (2.41) Т – постоянная времени, k – коэффициент усиления.
Применяя к (2.41) преобразование Лапласа при начальных нулевых условиях, получим операторное уравнение
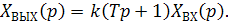(2.42)
Переходная функция звена
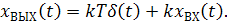(2.43)
Передаточная функция форсирующего звена на основании (2.42) запишется как
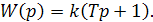(2.44)
Комплексный коэффициент передачи форсирующего звена получается путём замены p на jω в выражении (2.44):
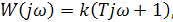(2.45)
или
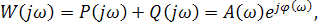(2.46)
где
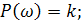
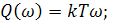
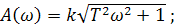
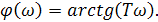(2.47)
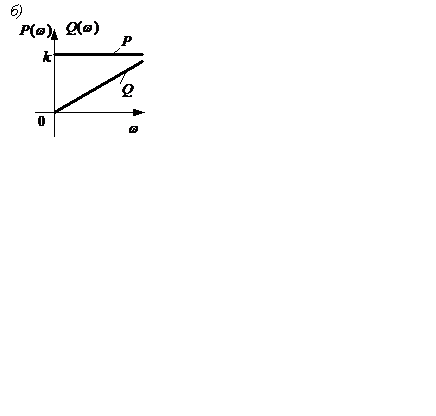
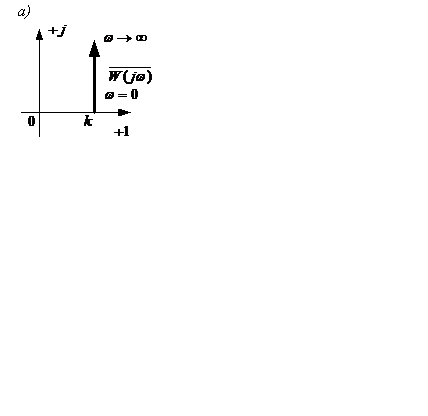Годограф W(jω) и частотные характеристики представлены на рисунке 2.15, а…в.
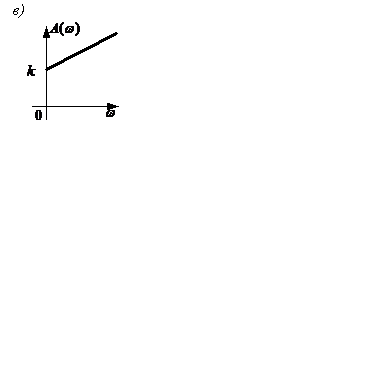
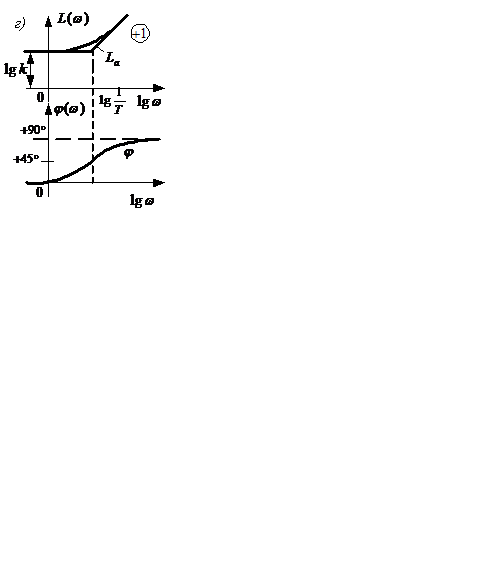
Рисунок 2.15
Логарифмическая амплитудно-фазовая характеристика
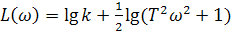. (2.48)
Асимптотические характеристики состоят из двух полупрямых
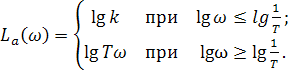(2.49)
Отсюда видно, прямая амплитудно-фазовая характеристика форсирующего звена аналогична инверсной характеристике инерционного звена первого порядка. Это, в свою очередь, отражается на точных логарифмических амплитудных и фазовых характеристиках (рисунок 2.15, г).
Так же, как и дифференцирующее звено, форсирующее звено в идеальном виде не может быть реализовано. В реальных форсирующих устройствах всегда имеются малые параметры, создающие инерционность; они характеризуются полиномом в знаменателе W(p), порядок которого выше, чем порядок числителя.
Дата добавления: 2014-12-22; просмотров: 5869;