Основные формулы и соотношения. 1) Концентрация внимания руководства на решающих работах.

1) Концентрация внимания руководства на решающих работах.

2) В любой момент руководство располагает исчерпывающей информацией.

3) Реализуется принцип непрерывности планирования хода работ и управления ими.

4) Система обеспечивает возможность рационального маневрирования выделенными для данной разработки ресурсами.

5) Устанавливается чёткая взаимосвязь между ответственными исполнителями отдельных работ.

ПСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ

Кафедра «Теоретические основы электротехники»

В.Г.Мацевич, Т.А.Федотова

" ИЗМЕРИТЕЛЬНАЯ ТЕХНИКА"

Методические указания и сборник задач

Псков

Г.

Часть 1. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ

Основные формулы и соотношения

1.1. Основной частью аналогового электроизмерительного прибора является измерительный механизм (ИМ). Его назначение преобразовать входную электрическую величину (ток, напряжений, мощность и т.д.) в угол отклонения указателя, который пропорционален размеру этой величины. Таким образом, выходной величиной ИМ является угол отклонения указателя, жестко связанного с подвижной частью ИМ. В зависимости от рода взаимодействия подвижной и неподвижной частей ИМ делятся на системы: магнитоэлектрическую, электромагнитную, электродинамическую, ферродинамическую, электростатическую, индукционную и др. Таким же образом на системы подразделяются и аналоговые измерительные приборы. Измерительные механизмы в сочетании с другими измерительными преобразователями, указателем и шкалой, проградуированной в единицах входной величины, образуют электроизмерительные приборы.

Подвижная часть прибора в процессе измерения входной величины испытывает воздействие нескольких моментов сил: вращающего, противодействующего, успокоения, трения. Наиболее общие выражения для этих моментов сил имеют вид:

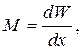
где W – энергия взаимодействия по координате х.

Момент вращения возникает в результате взаимодействия подвижной и неподвижной частей прибора:

,

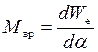где 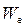- электромагнитная энергия взаимодействия, a - угол поворота подвижной части.

Противодействующий момент создается в результате воздействия на подвижную часть упругих элементов, закрепленных между подвижной и неподвижной частями:

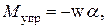
где w – коэффициент жесткости спиральной пружины; a - угол отклонения указателя от нулевого положения.

Момент успокоения создается с помощью специального успокоителя (демпфера):

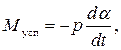
где р – коэффициент успокоения; 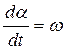- угловая скорость поворота подвижной части.

Момент сил трения стараются свести к нулю.

В результате воздействия этих моментов сил подвижная часть приобретает угловое ускорение и ее движение можно описать уравнением:

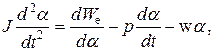
где 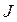- момент инерции подвижной части, 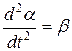- угловое ускорение.

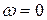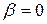При снятии показаний с прибора, подвижная часть его находится в покое, поэтому и . Уравнение прибора, когда его указатель находится в положении относительно нуля, соответствующем измеряемой величине, приобретает вид

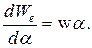
1.2. В соответствии с этим для магнитоэлектрического амперметра получим уравнение

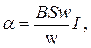
где 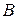- магнитная индукция в рабочем зазоре прибора; 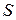- площадь рамки, состоящей из 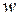витков провода; 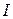- измеряемый ток.

Уравнение магнитоэлектрического вольтметра имеет вид

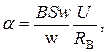
где 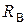- сопротивление вольтметра; 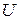- измеряемое напряжение.

Уравнения электромагнитных амперметра и вольтметра соответствуют выражениям

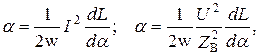
где 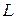- индуктивность катушки прибора; 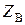- полное сопротивление вольтметра.

Уравнения электродинамических амперметра и вольтметра соответственно принимают вид

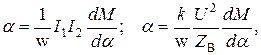
где 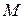- коэффициент взаимной индукции подвижной и неподвижной катушек прибора.

Уравнение электростатического вольтметра соответствует выражению

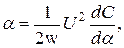
где С – емкость прибора.

Выражение

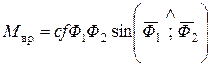
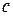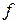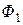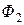соответствует уравнению индукционного измерительного механизма, который является основной частью счетчика электрической энергии. В выражении для вращательного момента, действующего на подвижный диск счетчика - постоянный коэффициент, - частота тока, и - магнитные потоки, пересекающие диск, ( 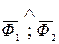) – угол сдвига фаз между магнитными потоками.

1.3. Помимо уравнения прибора важной характеристикой является его чувствительность к входной величине 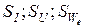. Общие выражения для чувствительностей по току и напряжению амперметров и вольтметров определяются как

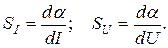
Применяя эти операции дифференцирования к написанным выше уравнениям приборов, получим:

- для магнитоэлектрических амперметра и вольтметра

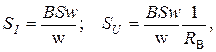
- для электромагнитных амперметра и вольтметра

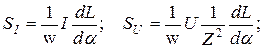
- для электродинамических амперметра и вольтметра

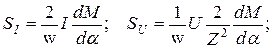
- для электростатического вольтметра

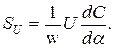
Чувствительность амперметров к току измеряется обычно в 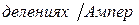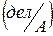, чувствительность вольтметров к напряжению обычно измеряется в .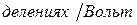

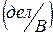1.4. Постоянная прибора. Величина, обратная чувствительности, называется постоянной прибора

.

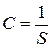Постоянная прибора равна отношению измеряемой велиины к отклонению подвижной части.

На практике часто вместо постоянной прибора пользуются термином цена деления, т. е. значением измеряемой величины, приходящимся на одно деление шкалы. Например:

,

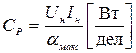где С_р - цена деления (или постоянная) ваттметра; U_н - номинальное напряжение ваттметра; I_н - номинальный ток ваттметра; 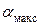- максимальное отклонение стрелки прибора в делениях шкалы.

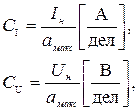
где С - цена деления, соответственно, амперметра и вольтметра; U_н, I_н -номинальные значения шкалы амперметра и вольтметра.

1.5. Мощность, потребляемая прибором. Для действия прибора расходуется электрическая мощность. При измерениях в цепях маломощных источников большое потребление мощности самим прибором может изменить режим цепи и привести к погрешностям. Поэтому малое потребление мощности приборами является достоинством рассматриваемых приборов.

Чтобы при включении амперметра происходило наименьшее изменение режима цепи, его сопротивление должно быть как можно меньше, так как затрачиваемая в нем мощность

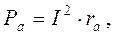
где I - ток, протекающий через амперметр; r_а - сопротивление амперметра.

Для вольтметра это требование удовлетворяется при наибольшем его сопротивления, так как затрачиваемая в нем мощность равна

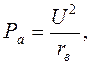
где U - напряжение на зажимах вольтметра; r_в - сопротивление вольтметра.

1.6. Погрешности приборов. Погрешности приборов делятся на две категории:

1) основная погрешность, обусловленная внутренними свойствами и качеством прибора. Эта погрешность наблюдается у приборов, находящихся в так называемых нормальных условиях: температура окружающей среды 20°С или указанная на шкале прибора; частота 50 Гц или указанная на шкале; нормальное положение прибора, обозначенное определенным знаком на шкале; отсутствие вблизи прибора ферромагнитных масс и внешних полей, кроме земного; номинальные напряжения и соsj. Эти условия соблюдаются при градуировании приборов;

2) дополнительные погрешности, вызванные отступлением от нормальных условий, обусловленные влиянием внешних факторов.

Для количественной оценки точности прибора вводятся три вида погрешностей:

а) абсолютная погрешность, представляющая собой разность между показанием прибора и действительным значе­нием измеряемой величины. Последнее обычно определяется по образцовому прибору.

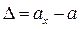
где 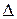- абсолютная погрешность, выражаемая в тех же единицах, что и измеряемая величина; 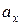- значение величины, измеренной прибором; 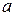- действительное значение измеряемой величины.

Абсолютная погрешность, взятая с обратным знаком, носит название поправки, обозначается g; поправка есть величина, которую надо алгебраически прибавить к показаниям прибора, чтобы получить действительное значение измеряемой величины:

.

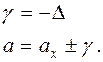б) относительная погрешность, представляющая собой отношение абсолютной погрешности к действительному значению измеряемой величины. Относительная погрешность, обозна­чаемая b (в некоторых книгах δ ) и обычно выражаемая в процентах, равна

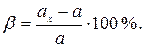
в) приведенная погрешность (в %), представляющая со­бой отношение абсолютной погрешности к максимальному зна­чению шкалы поверяемого прибора

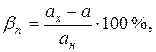
где 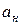- номинальное значение шкалы прибора. В некоторых книгах вместо 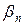используют обозначение .

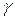Если прибор имеет двустороннюю шкалу, (с нулем посре­дине), то приведенную погрешность берут от суммы пределов, измерений по обе стороны от нуля.

1.7. Классы точности аналоговых приборов. Класс точности средства измерения определяет пределы допускаемых основной и дополнительной погрешностей. Эти пределы выражаются в форме приведенной относительной, относительной или абсолютной погрешностей. Если аддитивная погрешность средства измерений преобладает над мультипликативной, то класс точности выражается в виде приведенной относительной погрешности

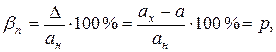
где р – отвлеченное положительное число, выбираемое из ряда 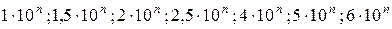(n = 1, 0, -1, -2, -3…). Для аналоговых приборов обычно р принимает значения 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4.

Нормирующее значение 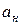принимается равным

a) конечному значению шкалы прибора, если нулевая отметка прибора находится на краю или вне шкалы;

b) номинальному значению, если прибор предназначен измерять величины, имеющие номинальное значение;

c) арифметической сумме конечных значений диапазона измерений, если прибор имеет двустороннюю шкалу, т.е. нулевая отметка находится на середине шкалы;

d) длине шкалы, если шкала резко нелинейная (гиперболическая, логарифмическая).

Если мультипликативная погрешность средства измерения преобладает над аддитивной, то класс точности выражается через относительную погрешность

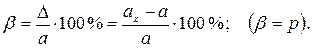
Для средств измерений с аддитивной и мультипликативной погрешностями класс точности выражается двучленной формулой

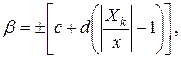
где 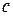и 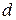- числа из приведенного выше ряда, причем 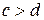, 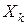- конечное значение диапазона измерений прибора, 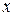- измеренное значение. Обычно такой способ выражения класса точности используется для цифровых приборов, многозначных мер и приборов сравнения.

Обозначение класса точности на средстве измерения в случае относительной приведенной погрешности выполняется в виде числа из приведенного ряда, например, 0,5; если шкала прибора существенно неравномерная, то класс точности обозначается в виде числа с галочкой, например 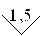, если класс точности выражается через относительную погрешность, то число из ряда заключается в скобки, например (2,5); если класс точности выражается по двучленной формуле, то класс точности выражается в виде дроби 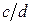, например 0,02/0,01.

1.8. Погрешности измерений. Погрешности измерений возникают вследствие несовершенства электроизмерительных приборов; из-за непостоянства условий, при которых происходили измерения; в результате ошибок экспериментаторов и т. д.

Погрешности измерения можно разделить на три класса:

а) систематические; б) случайные; в) промахи.

К систематическим погрешностям относятся:

- инструментальные погрешности, являющиеся следствием конструктивных недостатков измерительной аппаратуры, ее неисправности или неправильного градуирования;

- погрешности установки вследствие неправильного расположения измерительной аппаратуры (например, наличие вблизи электроизмерительных приборов магнитных полей, которые могут искажать показания приборов, и т. п.);

- личные погрешности, вызываемые индивидуальными особенностями наблюдателя;

- погрешности метода (теоретические погрешности), являющиеся следствием недостаточной теоретической обоснованности метода измерения или применения приближенных формул.

Приборные или инструментальные погрешности обусловлены несовершенством устройства приборов, наличием собственного входного сопротивления (у амперметров) или малым входным сопротивлением (у вольтметров), ограниченной точностью приборов, на что указывает их класс точности. Например, относительная погрешность измерения тока в цепи с сопротивлением 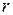при сопротивлении амперметра 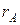равна

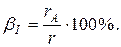
Относительная погрешность измерения напряжения на участке цепи сопротивлением 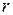при сопротивлении вольтметр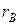а равна

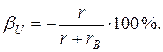
Эти формулы применимы и для измерения мощности и энергии электрического тока.

Инструментальная погрешность, обусловленная неточностью приборов, рассчитывается с помощью класса точности. Если класс точности прибора выражается через приведенную погрешность 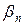, то относительная погрешность показания прибора будет равна для амперметра

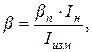
где 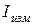- показание амперметра, 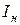- его номинальное значение.

Аналогично и для вольтметра

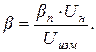
Если класс точности выражается через относительную погрешность 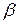, то погрешность показания равна классу точности прибора.

Дополнительные погрешности, так же относящиеся к систематическим инструментальным погрешностям, обусловлены отклонением условий измерений от нормальных. На показания приборов существенное влияние могут оказывать изменение температуры внешней среды, отклонение от нормальных значений частоты, формы кривой тока или напряжения и т.д.

Различные приборы в зависимости от принципа действия и конструкции по-разному реагируют на влияние внешних факторов.

Например, в магнитоэлектрических приборах изменение температуры окружающей среды приводит к следующим изменениям: изменяются сопротивления измерительной цепи, изменяются упругие свойства пружин, изменяются магнитные свойства постоянного магнита, но последние два явления почти полностью взаимно компенсируются.

В магнитоэлектрических приборах рамка делается из меди (реже из алюминия), сопротивление которой изменяется на 4% на каждые 10°С изменения температуры. Поэтому в простейшем случае, когда через рамку протекает весь измеряемый ток (в микроамперметрах и миллиамперметрах с пределами измерения, не превышающими 30-50 мА), изменение сопротивления рамки не вызывает погрешности в измерениях.

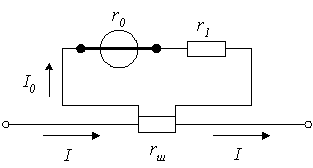
Рис. 1.

В схемах амперметров с шунтами, так как шунты делают из манганина (сопротивление манганина практически не зависит от температуры), приходится применять схемы температурной компенсации. В простейшем случае последовательно с рамкой включают сопротивление r₁ из манганина, рис. 1. Тогда температурный коэффициент сопротивления цепи рамки уменьшится и температурная погрешность будет 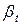определяться формулой

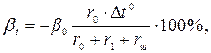
где β₀ —температурный коэффициент сопротивления цепи рамки;

r₀ — сопротивление рамки, пружинок и соединительных проводов;

r_ш — сопротивление шунта;

r₁ — добавочное сопротивление из манганина;

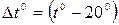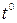; - температура во время измерения.

В приборах высокого класса точности применяют последовательно-параллельную схему температурной компенсации.

При отсутствии температурной компенсации

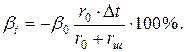
Температурная погрешность магнитоэлектрических вольтметров определяется формулой

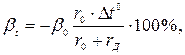
где r_Д - добавочное сопротивление из манганина.

Из формулы видно, что температурную погрешность вольтметра можно уменьшить, увеличивая добавочное сопротивление из манганина.

Для электромагнитных и электродинамических вольтметров температурная погрешность зависит от температурного коэффициента момента пружин и температурного коэффициента сопротивления катушек и определяется формулой

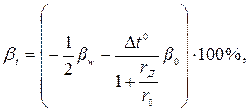
где 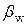- температурный коэффициент момента пружинок (он отрицателен и составляет 0,2¸0,3% на 10°С).

Второй член этого выражения зависит от предела измерения прибора. Наибольшей погрешностью обладает вольтметр на самом низком пределе измерения, т.к. 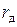в этом случае минимально.

В электродинамических амперметрах с последовательной схемой соединения катушек и в электромагнитных амперметрах температура влияет только на упругие свойства пружин. Поэтому температурная погрешность их не превышает ±0,2% на 10°С и не требует специальных способов компенсации.

На электродинамические и электромагнитные вольтметры существенное влияние оказывает частота. Главной причиной расхождения их показаний на постоянном и переменном токе является наличие индуктивного сопротивления .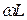

Частотная погрешность 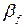при переходе от постоянного тока к переменному будет

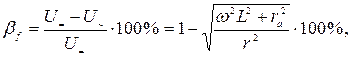
где r – сопротивление вольтметра на постоянном токе;

r_а – активное сопротивление цепи вольтметра на переменном токе.

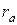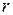При частотах до 2000 Гц, при которых работают эти приборы, можно считать отличие и , обусловленное вихревыми токами, в толще меди обмотки и окружающих металлических частях пренебрежимо малым. Тогда, принимая r_а 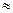r, получим:

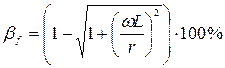
или

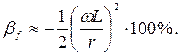
Для компенсации этой погрешности часть добавочного со­противления вольтметра (рис. 2) шунтируется емкостью С так, чтобы индуктивность цепи вольтметра стала малой. Однако при рассмотрении частотной погрешности электромагнитных вольтметров надо иметь в виду, что индуктивность изменяется с изменением угла отклонения и погрешность будет различной при различных показаниях. Поэтому частотная компенсация справедлива для одного показания, т. е. мало эффективна.

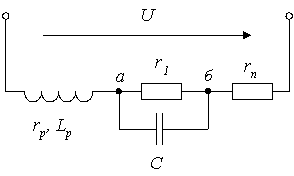
Рис. 2.

На электростатические вольтметры частота и форма кривой не влияют, и, кроме того, эти приборы обладают очень большим входным сопротивлением, определяемым по формуле

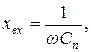
где С_п - емкость прибора.

Отклонение подвижной части выпрямительного прибора пропорционально средневыпрямленному значению протекающего через него тока. Поэтому измерить действующее значение переменного тока можно только в том случае, если известен коэффициент формы кривой переменного тока. Обычно шкалы выпрямительных приборов градуируются в действующих значениях при синусоидальной форме кривой, умножая для этого показания прибора на коэффициент формы 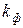=1,11 (так как для синусоиды ).

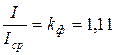Если формы кривой отличаются от синусоидальной, в показаниях возникает погрешность, присущая методу измерения

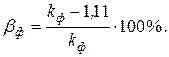
Методические погрешности обусловлены несовершенством метода измерения и, в частности, несовершенством схемы измерения. Так при косвенных измерениях сопротивления и мощности, потребляемой нагрузкой, методом амперметра и вольтметра обычно используют две схемы, рис. 3.

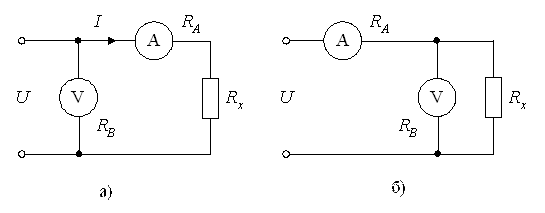
Рис. 3.

Погрешности измерения сопротивления ∆ 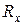и самого 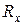по схеме а) равны

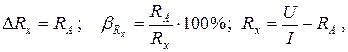
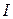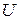где и показания приборов.

Погрешности измерения 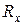по схеме б):

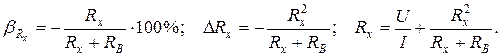
Субъективные или личные погрешности у опытных экспериментаторов обычно малы и ими пренебрегают по сравнению с другими составляющими суммарной систематической погрешности. Принято считать, что эта погрешность 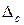не превышает 20% от постоянной прибора, т.е.

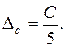
Систематические погрешности, в свою очередь, делятся на погрешности прямого и косвенного измерения. Относительная погрешность результата прямых измерений подсчитывается по формулам, приведенным в п. 2.8. Относительная погрешность косвенного измерения равна сумме относительных погрешностей каждого измерения

,

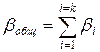где b_общ - погрешность косвенного измерения;

b_i – относительная погрешность каждого прямого измерения;

k – число приборов, используемых при косвенном измерении.

,

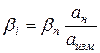где b_n – приведенная погрешность прибора, численно равная его классу;

а_н - номинальное значение шкалы прибора;

а_изм - значение величины, измеренной прибором.

Например, если для определения cosj воспользоваться показаниями ваттметра, амперметра и вольтметра, то относительная погрешность косвенного измерения cos j будет равна сумме относительных погрешностей каждого измерения:

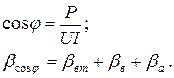
В свою очередь,

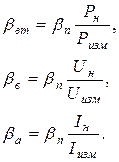
Или, если известны мощность и ток, протекающий в цепи, можно найти активное сопротивление и относительную погрешность его измерения:

.

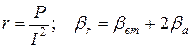Итак, при косвенном измерении надо определить погрешности показаний отдельных приборов, а затем подсчитать погрешность результата измерения.

Однако такой расчет погрешности является излишне завышенным. Более достоверным будет геометрическое сложение погрешностей, когда погрешность косвенного измерения определяется геометрическим сложением погрешностей прямых измерений

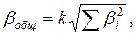
где 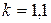. Приведенные выше формулы расчета относительной погрешности косвенных измерений пригодны для линейных функций типа

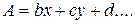
На практике чаще встречаются нелинейные функции. В этих случаях относительная погрешность косвенного измерения рассчитывают по формуле

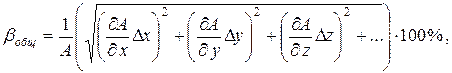
где 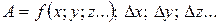- абсолютные погрешности аргументов косвенных измерений.

Независимо от того, каково происхождение систематической погрешности, результирующая суммарная неисключенная абсолютная систематическая погрешность 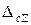представляет собой алгебраическую сумму составляющих

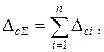
а суммарная неисключенная относительная погрешность равна

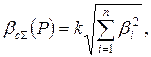
где Р – доверительная вероятность, 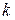- коэффициент, зависящий от 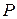; при ; .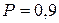

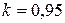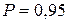
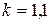Таким образом, систематические погрешности измерения при тщательной постановке опыта могут быть учтены и даже устранены.

Случайные погрешности контролю не поддаются, так как они появляются в результате одновременного действия многих различных причин. Эти погрешности подчиняются законам больших чисел, поэтому здесь возможен только статистический учет, подчиняющийся теории вероятностей.

Случайные погрешности обнаруживаются при многократных измерениях заданной величины в одних и тех же условиях.

1.9. Расширение пределов измерения. Шунты, подключаемые последовательно с нагрузкой в цепь измеряемого тока и параллельно с прибором, служат для расширения предела измерения прибора по току

,

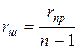где r_ш - сопротивление шунта;

r_пр - сопротивление прибора;

n - коэффициент шунтирования;

,

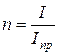где I - ток в неразветвленной части цепи, равный сумме токов: I=I_ш + I_пр;

I_ш - ток, протекающий через шунт; I_пр - ток, протекающий через рамку прибора (амперметра или измерительного механизма).

Добавочные сопротивления, соединяемые последовательно с прибором, дают возможность расширить его предел измерения по напряжению

,

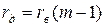где r_д – величина добавочного сопротивления;

r_в - сопротивление вольтметра;

m - коэффициент расширения предела измерения, равный

,

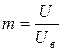где U - измеряемое напряжение;

U_в - напряжение, на которое рассчитан вольтметр.

Измерительные трансформаторы тока. У трансформаторов тока номинальный первичный ток, как правило, больше номинального вторичного, поэтому в них число витков w₁<w₂. Согласно нормам во всех измерительных трансформаторах тока номинальный вторичный ток равен 5 А (реже 1 А)

,

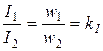где I₁ и I₂ - первичный и вторичный токи;

w₁ и w₂ - число витков в первичной и вторичной обмотках;

k₁ - действительный коэффициент трансформации трансформатора тока.

Определив по амперметру I₂, можно найти ток I₁

.

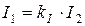Так как действительный коэффициент трансформации не остается строго постоянным, а зависит от режима работы трансформатора, т. е. от величины и частоты тока, характера и величины нагрузки вторичной цепи, качества материала сердечника, то в практике обычно пользуются номинальным коэффициентом трансформации, который всегда указывается на щитке трансформатора в виде дроби:

.

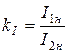Приближенное значение измеряемого тока равно

.

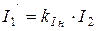Относительная погрешность трансформатора тока, происходящая из-за неравенства действительного и номинального коэффициентов трансформации, может быть определена из следующего выражения:

.

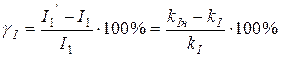Измерительные трансформаторы напряжения. Первичное номинальное напряжение в трансформаторах напряжения всегда больше вторичного номинального напряжения, поэтому в них w₁>w₂.

По принятым нормам вторичное номинальное напряжение равно 100 В

,

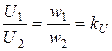где U₁ и U₂ - первичное и вторичное напряжения;

w₁ и w₂ - число витков в первичной и вторичной обмотках;

k_U - действительный коэффициент трансформации трансформатора напряжения;

Измеряемое напряжение равно U₁ = k_U ·U₂.

Так как измерительные трансформаторы тока и напряжения сходны по принципу своего действия, то по аналогии с трансформаторами тока можно написать

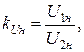
где k_Uн - номинальный коэффициент трансформации трансформатора напряжения;

U_1н, U_2н - номинальные значения первичного и вторичного напряжений, указанные на щитке трансформатора.

Приближенное значение измеряемого напряжения

.

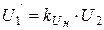Относительная погрешность трансформатора напряжения равна

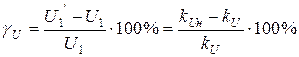
Конденсаторы. Для расширения пределов измерения электростатических вольтметров на переменном токе применяются конденсаторы, подключаемые к вольтметру последовательно (рис. 4а) или с конденсаторным делителем напряжения (рис. 4б)

,

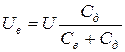где U_в - напряжение между электродами вольтметра;

U - измеряемое напряжение;

С_д - емкость добавочного конденсатора;

С_в - емкость самого вольтметра.

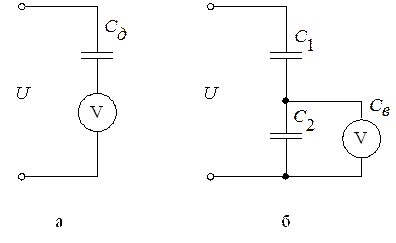
Рис. 4.

Емкость добавочного конденсатора может быть найдена из следующего выражения:

,

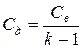где 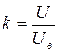называется коэффициентом расширения пределов измерения.

Для схемы 4б

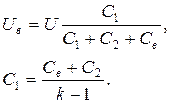
При С_в<С₂ отношение напряжений измеряемого и на зажимах вольтметра остается постоянным и характеристика шкалы вольтметра емкостным делителем напряжения не искажается. При выполнении указанного условия изменение частоты измеряемого напряжения и сопротивления изоляции конденсаторов очень мало влияют на показания вольтметра.

В цепях постоянного тока для расширения пределов измерения электростатического вольтметра применяется делитель напряжения, выполненный из проволочных или непроволочных сопротивлений (рис. 3)

,

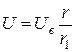откуда 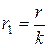, где U - измеряемое напряжение, U_e - напряжение на зажимах вольтметра, .

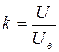В этой схеме сопротивление изоляции прибора должно быть значительно больше сопротивления r_1.

1.10. Магнитный поток, пронизывающий рамку магнитоэлектрического прибора

,

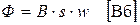где В - индукция в воздушном зазоре, Тл;

s - сечение рамки, м²;

w - число витков на рамке прибора.

1.11. Вращающий момент подвижной части магнитоэлектрического прибора

,

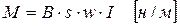где I – ток, протекающий по рамке, А.

1.12. Противодействующий момент прибора при повороте рамки на угол a

,

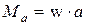где w - удельный противодействующий момент .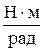

1.13. Коэффициент добротности (характеризующий механические свойства прибора)

,

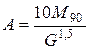где А - практический коэффициент добротности;

М₉₀ - противодействующий момент при повороте подвижной части на 90°;

G - вес подвижной части.

1.14. Магнитоэлектрические амперметры, вольтметры и омметры. Магнитоэлектрический измерительный механизм может быть без шунта включен последовательно в цепь измеряемого тока, если ток не превышает значения, допустимого для рамки прибора. При измерениях напряжений применяется тот же измерительный механизм, но последовательно с рамкой включается добавочное сопротивление.

При изменении окружающей температуры возникает добавочная погрешность от изменения сопротивления рамки, выполненной из медной проволоки, а также вследствие изменения со­противления, пружинок, создающих противодействующий момент. На рис. 6 даны схемы вольтметра и амперметра.

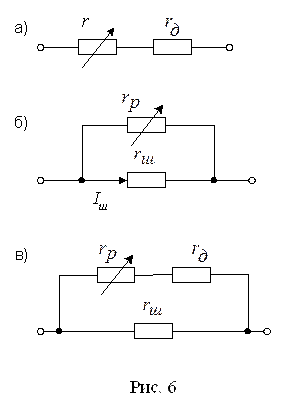
Для схемы рис. 6а справедливо следующее равенство:

,

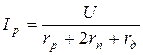где I_р - ток в рамке;

U - напряжение, приложенное к схеме;

r_р - сопротивление рамки;

r_п - сопротивление одной пружинки;

r_д - добавочное сопротивление из манганина.

С изменением окружающей температуры будут изменяться r_р и r_д.

Для схемы рис. 6б

,

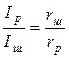где I_р - ток, протекающий через рамку прибора;

I_ш - ток, протекающий через шунт;

r_ш и r_p - сопротивления, соответственно, шунта и рамки с пружинками (прибора).

Так как по схеме рис. 6б изменения показаний от колебаний температуры значительны, то для уменьшения погрешности схему внутренних соединений амперметров осуществляют согласно рис. 6в. Тогда

,

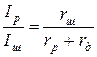где r_д - добавочное сопротивление из манганина, включенное последовательно с рамкой и пружинками. Расчет температурной погрешности см. в п. 2.8.

На рис. 7а изображена последовательная схема омметра. Величина тока в катушке такого омметра

,

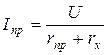(r_пр и r_х - сопротивления прибора и измеряемое).

На рис. 7б дана параллельная схема омметра

.

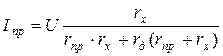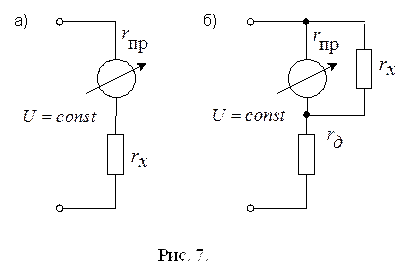
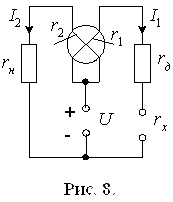
1.15. Логометры магнитоэлектрические. На рис. 8 изображена схема магнитоэлектрического логометра. Для этой схемы

,

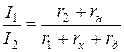где I₁, I₂ - токи, протекающие по рамкам;

r₁, r₂ - сопротивления рамок;

r_н - постоянное сопротивление;

r_д - добавочное сопротивление для защиты рамки от большого тока;

r_х - измеряемое сопротивление.

1.16. Магнитоэлектрические выпрямительные приборы. Для схемы с однополупериодным выпрямлением справедливо равенство

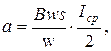
где a - отклонение подвижной части;

I_ср - средневыпрямленное значение тока, протекающего по рамке; для синусоидальных токов 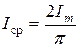, 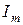- амплитудное значение выпрямленного тока.

Для схемы с двухполупериодным выпрямлением

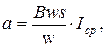
Обычно в цепях переменного тока приходится измерять действующее значение тока, которое связано со средневыпрямленным значением формулой

,

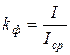где k_ф - коэффициент формы кривой;

I - действующее значение тока.

Заменив средне-выпрямленное значение тока действующим, имеем: для схемы с однополупериодным выпрямлением

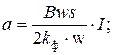
для схемы с двухполупериодным выпрямлением

.

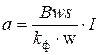Укажем значения коэффициентов формы кривых тока (напряжения) для наиболее часто встречающихся переменных периодических токов (напряжений). Для синусоидальных токов 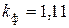; для токов прямоугольной формы (меандр) 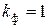; для токов треугольной формы 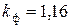. Значения коэффициентов амплитуды 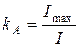для этих кривых соответственно равны 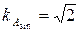; ; 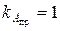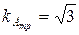. Для однополярных прямоугольных импульсов тока 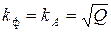, где 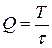- скважность импульсов.

1.17. Термоэлектрические преобразователи.ТермоЭДС 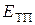термопар, используемых в измерительной технике, подчиняется уравнению

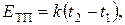
где 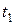- температура холодного спая, обычно находящего при температуре 0⁰С; 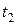- температура горячего спая, находящегося при температуре объекта, с которым она механически контактирует; 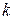- коэффициент, который указывается для различных термопар в справочниках.

Если температура холодного спая не равна 0⁰, то термоЭДС уменьшается и результат измерения с помощью термопары температуры оказывается заниженным. В этом случае необходимо в результат вводить поправку

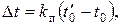
где 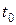- температура холодного спая, при которой градуировалась термопара (обычно 0⁰С); 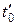- температура холодного спая термопары, при которой производилось измерение. Исправленное значение температуры горячего спая будет равно

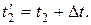
Обычно для термопар из благородных металлов и сплавов 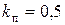, а для медных, константновых и т.д. термопар .

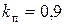Градуировочные таблицы или кривые, отражающие зависимость

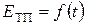
обычно приводятся в справочной литературе.

При измерении температуры с помощью термопар градуировку милливольтметров, измеряющих термоЭДС, следует производить с учетом того, что милливольтметр измеряет напряжение, а не ЭДС. И в данном случае также нужно вводить поправку 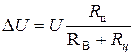, тогда ЭДС 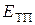будет равна

,

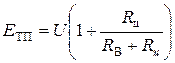где 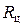- электрическое сопротивление термопары и проводов, соединяющих термопару с милливольтметром (сопротивление цепи); 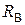- сопротивление вольтметра; U – показание милливольтметра.

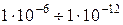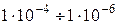1.18. Магнитоэлектрические гальванометры предназначены для измерения малых постоянных токов и напряжений А и В.

Разновидности гальванометров.

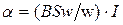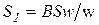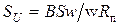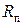Баллистические гальванометры предназначены для измерения электрических зарядов и магнитного потока. Уравнение магнитоэлектрического гальванометра имеет вид , а чувствительность ; , где - сопротивление гальванометра и цепи, куда включен гальванометр.

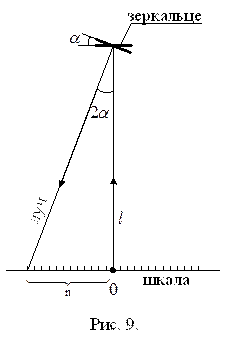У зеркальных гальванометров указателем является световой луч, а шкала отстоит от измерительного механизма на расстоянии 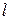метров (рис.9) Деления на шкалу наносятся через каждый 1 мм. Если при протекании тока I через гальванометр его подвижная часть отклонится от нулевого положения на угол 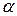(на такой же угол отклонится и зеркальце, расположенное на подвесе подвижной части), то световой луч, отраженный от зеркальца отклонится на угол 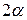. Из рисунка следует 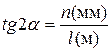. Обычно угол поворота подвижной части не превышает 5⁰, поэтому будет справедливо 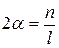. В этом случае чувствительность гальванометра по току будет равна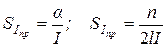 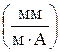. Это приведенная к расстоянию 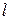чувствительность. Она не зависит от расстояния 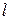. Обычная чувствительность гальванометра, численно равная отношению числа делений 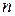на шкале при отклонении "зайчика" от нулевого положения при протекании по нему тока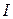 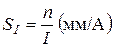зависит от расстояния 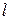и возрастает с ростом 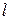. Чувствительность гальванометра по напряжению 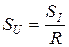, где 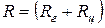- полное сопротивление цепи гальванометра, 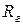- сопротивление гальванометра, 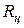- сопротивление цепи.

Для баллистического зеркального гальванометра при измерении электрических зарядов справедливо выражение

,

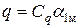где 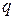- заряд, протекающий через гальванометр; 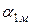- первое максимальное отклонение указателя гальванометра; 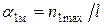; 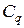- постоянная (цена деления) гальванометра по заряду (баллистическая постоянная по заряду).

Для этого же гальванометра при измерении магнитного потока получим

, ,

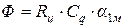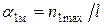где 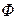- магнитный поток, 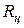- сопротивление цепи, в которую включен баллистический гальванометр. Коэффициент 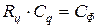называют баллистической постоянной гальванометра по магнитному потоку. Для критического режима работы гальванометра обычно указываются (на шильдике) значения 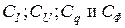. Коэффициент успокоения гальванометров вычисляется по формуле

.

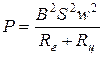1.19. Вращающий момент электродинамического прибора на постоянном токе

,

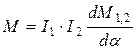где I₁, I₂ - токи в неподвижной и подвижной катушках; M_1,2 - взаимная индуктивность между катушками.

Вращающий момент прибора на переменном токе

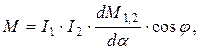
где I₁, I₂ - действующие значения токов в катушках; j - сдвиг по фазе между токами I₁ и I₂.

1.20. Взаимная индуктивность между катушками электродинамического прибора

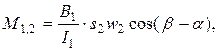
где В₁ - магнитная индукция поля неподвижной катушки; I₁ - ток в неподвижной катушке; s₂, w₂ - площадь и число витков подвижной катушки; b - угол между плоскостями катушек в начальном положении, т. е. при выключенном приборе; a - угол отклонения подвижной катушки.

1.21. Энергия магнитного поля катушек электродинамического прибора

,

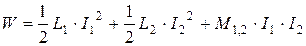где L₁ и L₂ - индуктивности катушек.

В электродинамических вольтметрах катушки соединяются последовательно, поэтому выражение для энергии магнитного поля катушек имеет вид

.

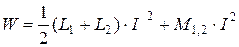1.22. Вращающий момент электромагнитного прибора на переменном токе

,

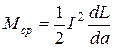где I - действующее значение тока в катушке; L - индуктивность катушки.

1.23. Вращающий момент индукционных приборов

,

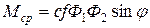где с - коэффициент пропорциональности; f - частота тока; Ф₁, Ф₂ - потоки, создаваемые токами, протекающими по обмоткам двух электромагнитов; j - сдвиг по фазе между потоками Ф₁ и Ф₂.

ЗАДАЧИ

1. Вычислить номинальное напряжение, потребляемую мощность и чувствительность магнитоэлектрического вольтметра, если номинальный ток в рамке прибора 5 мА, сопротивление рамки 50 Ом, сопротивление добавочного резистора 30 кОм, величина магнитной индукции в рабочем зазоре приборе 0,1 Тл, площадь рамки 2 см², число витков в рамке 150, жесткость пружины 1·10^-5 .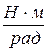

2. Магнитоэлектрический измерительный механизм имеет рамку сопротивлением 40 Ом и номинальный ток 5 мА. Шкала механизма – 100 делений. Для измерения тока к измерительному механизму присоединен шунт сопротивлением 0,201 Ом. Определить номинальный ток амперметра, его чувствительность и потребляемую мощность.

3. Электромагнитный миллиамперметр на 100 мА имеет 100 делений шкалы, сопротивление прибора 30 Ом; жесткость упругих элементов 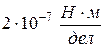; производная 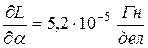. Определить величину вращающего момента и чувствительность прибора при токе 75 мА и потребляемую прибором максимальную мощность.

4. Даны два магнитоэлектрических прибора: вольтметр с верхним пределом измерения 150 В и шкалой, имеющей 100 делений; милливольтметр с верхним пределом измерения 75 мВ и шкалой, имеющей 100 делений.

Определить чувствительность к напряжению этих приборов. Установить, во сколько раз чувствительность к напряжению милливольтметра больше чувствительности вольтметра.

Решение. Чувствительность вольтметра к напряжению

.

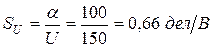Чувствительность милливольтметра к напряжению

.

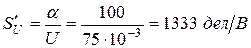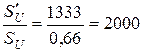, т.е. чувствительность к напряжению милливольтметра в 2000 раз больше.

5. Электродинамический ваттметр изготовлен на предел измерения по напряжению 150 В и по току 5 А; шкала прибора имеет 150 делений. Определить цену деления шкалы ваттметра.

6. Даны: магнитоэлектрический амперметр с верхним пределом. измерения 10 А и шкалой, имеющей 100 делений, и магнитоэлектрический миллиамперметр на 100 мА со шкалой, имеющей 50 делений.

Сравнить чувствительность к току обоих приборов.

Решение. Чувствительность к току амперметра

.

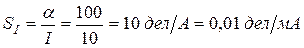Чувствительность к току миллиамперметра

.

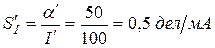Чувствительность миллиамперметра в 50 раз больше чувствительности амперметра, т.е.

.

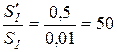7. Магнитоэлектрический прибор имеет номинальное напряжение 75 мВ, сопротивление рамки 10 Ом, шкалу на 100 делений.

Определить его чувствительность к току и напряжению.

Решение. Для определения чувствительности прибора к току надо найти ток, протекающий через его рамку при номинальном напряжении, т.е.

.

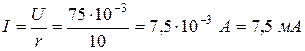Чувствительность прибора к току

.

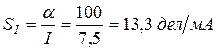Чувствительность прибора к напряжению

.

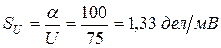8. Магнитоэлектрический прибор со шкалой на 100 делений имеет сопротивление рамки 20 Ом и чувствительность к току 2 дел/мА.

Определить предел измерения по напряжению и цену деления прибора в вольтах.

Решение. Зная число делений шкалы прибора и чувствительность к току, можно найти номинальный ток, протекающий через прибор, т.е.

.

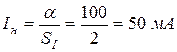Затем можно найти номинальное напряжение (предел измерения) прибора

.

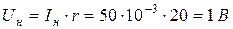Цена деления прибора будет равна

.

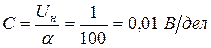9. Падение напряжения на рамке магнитоэлектрического миллиамперметра, имеющей сопротивление 10 Ом, при номинальном токе равно 75 мВ.

Как изменится чувствительность прибора к току, если подключить к нему шунт, сопротивление которого равно 0,53 Ом?

Решение. Определим номинальный ток, протекающий через прибор (без шунта)