Часть 4. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
4.1. Прямые измерения с многократными измерениями.
Правила обработки результатов измерения с многократными наблюдениями учитывают следующие факторы:
- обрабатывается ограниченная группа из n наблюдений;
- результаты наблюдений xi могут содержать систематическую погрешность;
- в группе наблюдений могут встречаться грубые погрешности;
- распределение случайных погрешностей может отличаться от нормального.
Обработка результатов наблюдений производится в следующей последовательности:
1. Исключить известные систематические погрешности из результатов наблюдений (введением поправки).
2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:
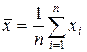 .
.
3. Вычислить оценку среднего квадратического отклонения результатов наблюдения 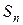 (СКО)
(СКО)
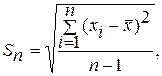
где 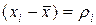 - называется остаточной суммой.
- называется остаточной суммой.
Вычислив оценку СКО результатов наблюдений, целесообразно проверить наличие в группе наблюдений грубых погрешностей (промахов), помня, что при нормальном законе распределения ни одна случайная погрешность хi - 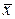 , с вероятностью практически равной единице, не может выйти за пределы ±3σ. Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления
, с вероятностью практически равной единице, не может выйти за пределы ±3σ. Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления 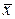 и
и 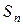 .
.
4. Вычислить оценку СКО результата измерения 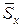 по формуле
по формуле
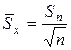 .
.
5. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению.
При числе наблюдений п < 15 принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону.
6. Вычислить доверительные границы ε случайной погрешности результата измерения при заданной вероятности Р:
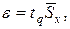
где tq — коэффициент Стьюдента (см. Таблицу 1), зависящий от n и P.
7. Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерений 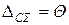 .
.
Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др.
При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении неисключенных систематических погрешностей границы, неисключенной систематической погрешности результата измерения 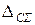 вычисляют по формуле
вычисляют по формуле
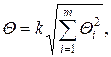
где 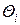 - граница i-й неисключенной составляющей систематической погрешности; k — коэффициент, определяемый принятой доверительной вероятностью (при Р = 0,95 k = 1,1); т — количество не исключенных составляющих.
- граница i-й неисключенной составляющей систематической погрешности; k — коэффициент, определяемый принятой доверительной вероятностью (при Р = 0,95 k = 1,1); т — количество не исключенных составляющих.
Доверительную вероятность для вычисления границ НСП принимают той же, что при вычислении границ случайной погрешности результата измерения.
8. Вычислить доверительные границы погрешности результата измерения.
Анализ соотношения между неисключенной систематической погрешностью и случайной погрешностью показывает, что если 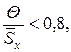 то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата Δ равным ±
то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата Δ равным ± 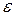 . Если
. Если 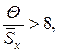 то случайной погрешностью можно пренебречь и принять границы погрешности результата Δ равным ±
то случайной погрешностью можно пренебречь и принять границы погрешности результата Δ равным ± 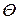 .
.
Если оба неравенства не выполняются, вычисляют СКО результата как сумму неисключенной систематической погрешности и случайной составляющей:
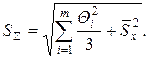 (*)
(*)
Границы погрешности результата измерения в этом случае вычисляют по формуле
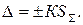 (**)
(**)
Коэффициент К вычисляют по эмпирической формуле
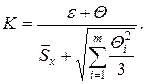 (***)
(***)
Стандартом регламентирована и форма записи результатов измерений. При симметричном доверительном интервале погрешности результат измерения представляют в форме Х ± Δ, Р, где Х — результат измерения.
При отсутствии данных о видах функции распределения составляющих погрешности результата или при необходимости дальнейшей обработки результатов, результат измерения представляют в форме X, 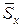 , n,
, n, 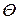 .
.
При анализе результатов наблюдений не всегда просто определить, является ли какое либо значение ряда наблюдений грубой погрешностью. Для обнаружения такого вида промахов используют статистический критерий. Таким критерием служит соотношение
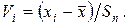
Если
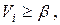
то результат является промахом и отбрасывается из ряда и обработка результатов производится вновь для ряда результатов, состоящего из 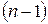 членов. Значения
членов. Значения 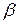 для данного
для данного 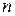 и принятой вероятности
и принятой вероятности 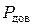 берут из таблицы 2.
берут из таблицы 2.
Оценивая точность измерения, не всегда достаточно определить числовое значение случайной погрешности 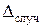 (особенно при ограниченном числе измерений n). В таких случаях задача сводится и к оценке пределов (доверительного интервала
(особенно при ограниченном числе измерений n). В таких случаях задача сводится и к оценке пределов (доверительного интервала 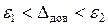 ), в которых с заданной (доверительной) вероятностью Р лежат значения погрешности
), в которых с заданной (доверительной) вероятностью Р лежат значения погрешности 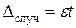 .
.
Доверительный интервал 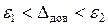 включает истинное значение
включает истинное значение 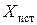 измеряемой величины с доверительной вероятностью
измеряемой величины с доверительной вероятностью
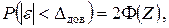
где 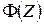 - функция Лапласа (интеграл вероятности), значения которой табулированы (табл. 3);
- функция Лапласа (интеграл вероятности), значения которой табулированы (табл. 3); 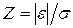 , где
, где 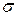 - срднее квадратическое отклонение результатов (СКО).
- срднее квадратическое отклонение результатов (СКО).
Вероятность того, что случайная погрешность окажется за границами интервала 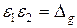
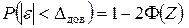
и называется уровнем значимости. При 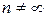 вместо
вместо 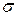 обычно принимают
обычно принимают 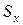 - оценку среднего квадратического отклонения результатов ряда измерений.
- оценку среднего квадратического отклонения результатов ряда измерений.
4.2. Прямые однократные измерения с точным оцениванием погрешности.
Подавляющее большинство технических измерений являются однократными. В обычных производственных условиях их точность может быть вполне приемлемой, а простота, высокая производительность (количество измерений в единицу времени) и низкая стоимость ставят однократное измерение вне конкуренции с любыми другими.
При однократных измерениях для получения результата измерения используется одно-единственное значение отсчета показаний прибора. Будучи по сути дела случайным, однократный отсчет х включает в себя инструментальную, методическую и личную составляющие погрешности измерения, в каждой из которых могут быть выделены систематические и случайные составляющие.
При измерении с точным оцениванием погрешности проблема заключается в выявлении и оценке систематических и случайных составляющих погрешностей с последующим их раздельным суммированием.
Особенностью однократного измерения является то, что законы распределения случайных составляющих неизвестны и представление о них приходится формировать на основе ограниченной априорной информации, а иногда и волевым порядком.
Сравнительно легко, путем поверки или по паспортным данным может быть получена оценка систематической погрешности прибора, а анализом метода измерения — оценка систематической погрешности методического происхождения. При наличии в документации на прибор сведений о дополнительных систематических погрешностях, обусловленных влияющими величинами, эти погрешности также оцениваются и учитываются.
После исключения из отсчета всех известных систематических погрешностей можно полагать, что погрешность исправленного результата хиспр состоит из неисключенных остатков систематических погрешностей и случайных составляющих погрешностей. Неисключенные систематические погрешности переводят в категорию случайных и оценивают каждую составляющую своими границами. При этом рекомендуется распределение вероятностей принимать равномерным, если погрешности заданы границами и нормальным, если заданы средним квадратическим отклонением.
В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допустимых основных и дополнительных погрешностей средств измерений, применявшихся при поверке в качестве образцовых, погрешности расчетных поправок и др.
Если неисключенные систематические погрешности оценены своими границами 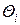 , то доверительные границы суммарной неисключенной систематической погрешности определяют по формуле
, то доверительные границы суммарной неисключенной систематической погрешности определяют по формуле 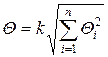 .
.
Составляющие случайных погрешностей могут быть заданы оценками средних квадратических отклонений 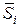 , найденными предварительно опытным путем по результатам многократных наблюдений, либо доверительными границами Δхi. В первом случае доверительные границы
, найденными предварительно опытным путем по результатам многократных наблюдений, либо доверительными границами Δхi. В первом случае доверительные границы 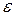 результирующей случайной погрешности результата определяются по формуле
результирующей случайной погрешности результата определяются по формуле
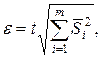
где 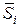 — оценка СКО i-й составляющей, t — коэффициент, зависящий от доверительной вероятности и числа наблюдений. В качестве t можно использовать коэффициент Стьюдента, соответствующий оценке той составляющей, которая вычислена по меньшему числу наблюдений.
— оценка СКО i-й составляющей, t — коэффициент, зависящий от доверительной вероятности и числа наблюдений. В качестве t можно использовать коэффициент Стьюдента, соответствующий оценке той составляющей, которая вычислена по меньшему числу наблюдений.
Если же случайные составляющие погрешности заданы доверительными границами Δxi, отвечающими одной и той же вероятности, то доверительные границы случайной погрешности результата вычисляют по формуле
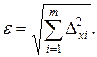
Получив по отдельности оценки неисключенной систематической и случайной погрешностей результата однократного измерения, целесообразно сопоставить их между собой. В случае, когда оказывается необходимым учитывать обе составляющие, суммирование их выполняется по формуле
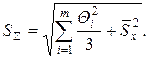
Как и при измерениях с многократными наблюдениями однократный отсчет показаний может содержать грубую погрешность. Во избежание грубой погрешности однократное измерение рекомендуется повторить 2 — 3 раза, приняв за результат среднее арифметическое. Статистической обработке эти отсчеты не подвергаются. Результат однократного измерения записывается в форме хиспр ± Δ, где 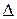 вычисляется по формулам (**) и (***).
вычисляется по формулам (**) и (***).
4.3. Однократные измерения с приближенным оцениванием погрешности.
Для таких измерений в качестве результата измерения принимают значение отсчета х, а оценивание погрешностей производится на основе нормативных данных о свойствах используемых средств измерений (пределов допускаемой основной погрешности, дополнительных погрешностей и др.). Поскольку эти данные относятся к множеству средств измерения данного типа, то у конкретного экземпляра прибора, используемого в измерении, действительные свойства могут значительно отличаться от нормированных. Тем не менее, не имея другой достоверной информации о реальных метрологических характеристиках, мы вынуждены производить оценку погрешности измерения на основе предельных норм. Такие оценки хотя и грубо, но все же дают возможность оценить погрешность сверху; но для корректировки результата измерения, для введения поправок они недостаточно надежны.
Общую схему оценивания погрешностей можно представить следующим образом. Выбрав, исходя из условий измерительной задачи, необходимое средство измерения (прибор), уточняют условия измерения (нормальные, рабочие) и оценивают возможные дополнительные погрешности прибора, возникающие от воздействия влияющих величин.
В результате для оценивания погрешности измерения имеем сведения о погрешностях средства измерения:
предел допускаемой основной погрешности прибора Δпр;
дополнительные погрешности Ψ1, …, Ψm.
Методические погрешности должны быть учтены заранее. Личные погрешности при измерениях предполагаются малыми и их не учитывают.
Таким образом, задача сводится к суммированию составляющих погрешности Δпр , Ψ1, …, Ψm.
Верхняя оценка погрешности результата измерения ΔΣ (без учета знака) может быть найдена суммированием составляющих по абсолютной величине:
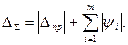
Более реальная оценка погрешности может быть получена статистическим сложением составляющих погрешности. Поскольку основная и дополнительные погрешности средства измерения заданы границами, то, считая их случайными величинами с равномерным распределением, границы их суммы вычислим по формуле 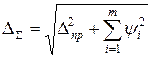 .
.
4.4. Косвенные измерения.
При косвенных измерениях искомое значение величины находят расчетом на основе измерения других величин, связанных с измеряемой величиной известной зависимостью
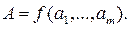 (1)
(1)
Результатом косвенного измерения является оценка величины А, которую находят подстановкой в предыдущую формулу оценок аргументов аi.
Поскольку каждый из аргументов аi, измеряется с некоторой погрешностью, то задача оценивания погрешности результата сводится к суммированию погрешностей измерения аргументов. Однако особенность косвенных измерений состоит в том, что вклад отдельных погрешностей измерения аргументов в погрешность результата зависит от вида функции.
Для оценки погрешностей существенно разделение косвенных измерений на линейные и нелинейные косвенные измерения. При линейных косвенных измерениях уравнение измерений имеет вид
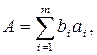 (2)
(2)
где bi — постоянные коэффициенты при аргументах аi.
Любые другие функциональные зависимости относятся к нелинейным косвенным измерениям.
Результат линейного косвенного измерения вычисляют по формуле (2), подставляя в нее измеренные значения аргументов.
Погрешности измерения аргументов могут быть заданы своими границами Δai, либо доверительными границами Δa(P)i, с доверительными вероятностями Рi.
При малом числе аргументов (меньше пяти) простая оценка погрешности результата ΔA получается суммированием предельных погрешностей (без учета знака), т.е. подстановкой границ Δа1, Δа2, … , Δаm в выражение
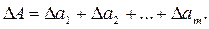
Однако эта оценка является излишне завышенной, поскольку такое суммирование фактически означает, что погрешности измерения всех аргументов одновременно имеют максимальное значение и совпадают по знаку. Вероятность такого совпадения практически равна нулю. Для нахождения более реалистичной оценки переходят к статистическому суммированию погрешностей аргументов. Полагая, что в заданных границах погрешности аргументов распределены равномерно, доверительные границы ΔА(Р) погрешности результата измерения рассчитывают по формуле
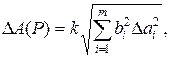
где коэффициент k =1,1 при Р = 0,95.
Если погрешности измерения аргументов заданы доверительными границами с одинаковыми доверительными вероятностями, то полагая распределение этих погрешностей нормальным, доверительные границы результата находят по формуле
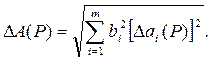
При различных доверительных вероятностях погрешностей аргументов их необходимо привести к одному и тому же значению Р.
Нелинейные косвенные измерения характеризуются тем, что результаты измерений аргументов подвергаются функциональным преобразованиям. Но, как показано в теории вероятностей, любые, даже простейшие функциональные преобразования случайных величин, приводят к изменению законов их распределения. В этом случае приходится ограничиваться приближенной оценкой границ погрешности результата косвенных измерений. В основе приближенной оценки погрешности нелинейных косвенных измерений лежит линеаризация функции 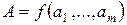 и дальнейшая обработка результатов, как при линейных измерениях. Исходя из выше написанного, приближенное значение абсолютной погрешности результата косвенного измерения
и дальнейшая обработка результатов, как при линейных измерениях. Исходя из выше написанного, приближенное значение абсолютной погрешности результата косвенного измерения 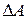 будет равно
будет равно
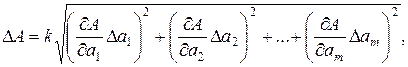
где k = 1,1 при доверительной вероятности Р = 0,95.
Относительная погрешность результата косвенного измерения (в процентах)
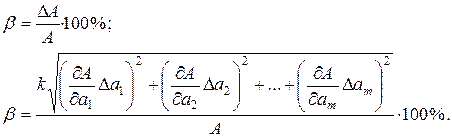
При этом предполагается, что распределение погрешностей аргументов функции подчиняется равномерному закону.
ЗАДАЧИ
141. Шестикратное измерение сопротивления резистора дало следующие результаты: 72,361; 72,357; 72,352; 72,344; 72,345.
Найти результат измерения и доверительный интервал его при вероятности Р = 0,99. Будем считать, что неисключенные систематические, погрешности очень малы по сравнению со случайными. Результаты подчиняются распределению Стьюдента.
Решение:
а) Находим среднее арифметическое результатов:
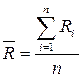 ;
; 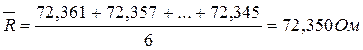 .
.
б) Находим остаточные суммы ri;
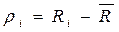 ;
; 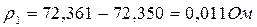
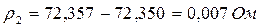
…………………………………..
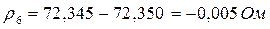 .
.
в) Находим сумму квадратов остаточных сумм:
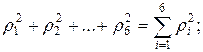
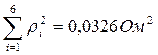 .
.
г) Определим оценку среднего квадратического отклонения результатов измерений:
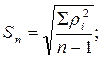
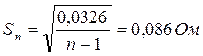 .
.
д) Определим оценку среднего квадратического отклонения среднего результата (результата измерения):
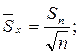
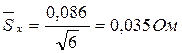 .
.
е) Для n = 6 и Р = 0,99 коэффициент Стьюдента (по таблице № 1) равен t = 4,03.
Доверительный интервал результата измерения
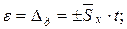
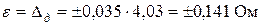 .
.
ж) Результат измерения запишется в виде:
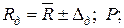

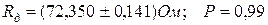 ,
,
где Rд – действительное значение сопротивления.
142. Получен ряд наблюдений при измерении сопротивления тензодатчика для определения величины деформации детали: 9,992; 9,995; 9,997; 9,999; 10,000; 10,001; 10,003; 10,005; 10,007; 10,121 Ом.
Определить есть ли промахи при данных измерениях?
Решение:
Подозрительным является результат 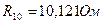 , т.к. он по величине отличается от остальных.
, т.к. он по величине отличается от остальных.
Определим среднее арифметическое значение сопротивления тензодатчика:
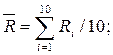
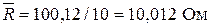 .
.
Определим оценку среднего квадратического отклонения результатов.
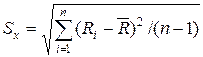 ;
; 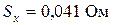 .
.
Подозрительный результат (в нашем случае десятый) можно считать промахом, если 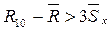 (правило трех сигма).
(правило трех сигма).
Проверяем: 10,121-10,012 = 0,109 = 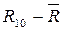
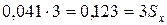
Данный результат не является промахом, т.к. 0,109>0,123 (Ом).
143. Определить мощность, выделяющуюся на резисторе 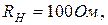 если падение напряжения на нем равно
если падение напряжения на нем равно 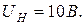 Погрешность измерения сопротивления
Погрешность измерения сопротивления 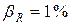 .
.
Определить абсолютную и относительную погрешности измерения мощности. Погрешность измерения напряжения 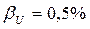 .
.
Решение:
Мощность определим по формуле:
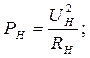
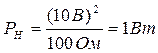 .
.
Относительная погрешность измерения может быть вычислена по формуле:
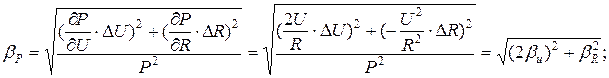
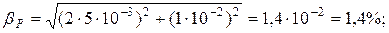
т.к. 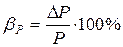 , то
, то 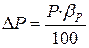 ,
, 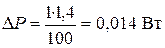 .
.
144. Пусть цена деления равномерной шкалы равна Хд единиц измеряемой физической величины, длина деления равна Lд мм. Определить наибольшее значение личной погрешности 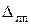 .
.
Решение:
При условии, что средний оператор может интерполировать в пределах деления шагами по 0,2 деления, т.е. по 0,2Lд, наибольшее значение личной погрешности
 Δлп = Хд · 0,2Lд/Lд = 0,2Хд.
Δлп = Хд · 0,2Lд/Lд = 0,2Хд.
145. Напряжение источника ЭДС Ux с внутренним сопротивлением Ri = 60±10 Ом измерено вольтметром класса точности 0,5. Сопротивление вольтметра RВ = 5 кОм и известно с погрешностью ±0,5%. Показание вольтметра UВ = 12,35 В. Найти поправку, которую нужно внести в показание прибора для определения действительного значения напряжения источника ЭДС.
Решение:
Показания вольтметра соответствуют падению напряжения на нем:
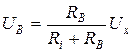 .
.
Относительная систематическая методическая погрешность, обусловленная ограниченным значением сопротивления RВ,
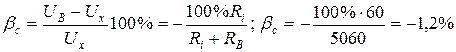 .
.
Поправка к показанию вольтметра равна абсолютной погрешности, взятой с обратным знаком. Т.к. 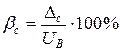 , то
, то 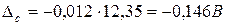 ;
; 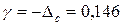 . Погрешность полученного значения поправки определяется погрешностью, с которой известно сопротивление Ri. Ее предельное значение составит
. Погрешность полученного значения поправки определяется погрешностью, с которой известно сопротивление Ri. Ее предельное значение составит 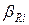 = 10/60=0,167. Погрешностью из-за неточности оценки RВ, равной 0,005, можно пренебречь. Следовательно, погрешность определения поправки
= 10/60=0,167. Погрешностью из-за неточности оценки RВ, равной 0,005, можно пренебречь. Следовательно, погрешность определения поправки 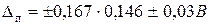 .
.
Таким образом, поправка, которую необходимо ввести в показания вольтметра с учетом округления  = + 0,15B. Тогда исправленное значение U’x = 12,35 + 0,15 = 12,50B. Этот результат имеет определенную погрешность, обусловленную допустимой погрешностью вольтметра и, в том числе, неисключенный остаток систематической погрешности Δ = ± 0,03 В или
= + 0,15B. Тогда исправленное значение U’x = 12,35 + 0,15 = 12,50B. Этот результат имеет определенную погрешность, обусловленную допустимой погрешностью вольтметра и, в том числе, неисключенный остаток систематической погрешности Δ = ± 0,03 В или 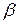 = ±0,24% из-за потребления некоторой мощности вольтметром.
= ±0,24% из-за потребления некоторой мощности вольтметром.
146. Оценить погрешность результата однократного измерения напряжения U = 0,9 В на сопротивлении R = 4 Ом, выполненного вольтметром класса точности 0,5 с верхним пределом измерения Uн = 1,5 В и внутренним сопротивлением RВ = 1000 Ом. Известно, что дополнительные погрешности показаний вольтметра из-за магнитного поля и температуры не превышают соответственно 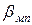 = ±0,75% и
= ±0,75% и 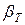 = ±0,3%.
= ±0,3%.
Решение:
Предел допускаемой относительной погрешности вольтметра на отметке 0,9 В составляет
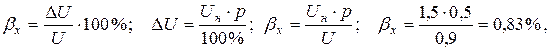
где р – класс точности вольтметра.
Это неисключенная систематическая погрешность, обусловленная основной погрешностью вольтметра.
При подсоединении вольтметра исходное напряжение Ux изменяется из-за наличия RВ. Показание вольтметра будет равно:
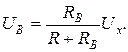
Тогда методическая погрешность, обусловленная конечным значением RВ, в относительной форме

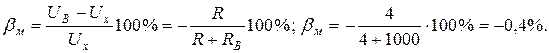
Данная погрешность является систематической и должна быть внесена в результат в виде поправки. Поправка в абсолютной форме на отметке 0,9 В равна 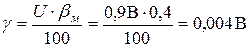 . Тогда результат измерения с учетом поправки Uх = 0,9 + 0,004 = 0,904В.
. Тогда результат измерения с учетом поправки Uх = 0,9 + 0,004 = 0,904В.
Поскольку основная и дополнительная погрешности заданы своими граничными значениями, то они могут рассматриваться как неисключенные систематические погрешности и соответственно суммироваться по формуле 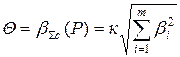 , где Р - доверительная вероятность, k – коэффициент, зависящий от Р; при Р = 0,9 k = 0,95, при Р = 0,95 k = 1,1. При доверительной вероятности 0,95 доверительная граница неисключенной систематической погрешности
, где Р - доверительная вероятность, k – коэффициент, зависящий от Р; при Р = 0,9 k = 0,95, при Р = 0,95 k = 1,1. При доверительной вероятности 0,95 доверительная граница неисключенной систематической погрешности 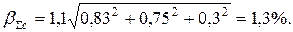
В абсолютной форме 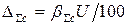 = 0,012 B. Окончательный результат измерения с учетом округления записывается в виде U = 0,9 B; Δ = ±0,01B; P = 0,95.
= 0,012 B. Окончательный результат измерения с учетом округления записывается в виде U = 0,9 B; Δ = ±0,01B; P = 0,95.
147. Цифровым измерителем иммитанса Е7-14 проводились прямые многократные измерения сопротивления магазина сопротивлений марки Р33, номинальное значение которого равно 0,1Ом. Измерения проводились в диапазоне рабочих температур измерителя иммитанса. Получены следующие результаты измерения Ri: 145,44; 145,36; 145,43; 145,38; 145,44; 145,42; 145,41; 145,39; 145,40; 145,41; 145,45; 145,43; 145,46; 145,37; 145,48 мОм.
Для устранения влияния соединительных проводов и переходных сопротивлений контактов был проведен ряд измерений при нулевом значении магазина сопротивлений. Получены следующие результаты измерения R0i: 45,30; 45,29; 45,28; 45,29; 45,28; 45,30; 45,30; 45,30; 45,30; 45,31; 45,32; 45,30 мОм.
Требуется провести обработку результатов измерений. Найти суммарную погрешность измерения сопротивлений.
Решение:
Суммарная погрешность измерения сопротивления складывается из случайной и систематической погрешностей. Систематическая погрешность измерения сопротивления состоит из трех составляющих, обусловленных:
1) ненулевым значением сопротивления соединительных проводов и переходных контактов зажимов используемых средств измерений;
2) основной погрешностью, обусловленной классом точности прибора;
3) дополнительной погрешностями измерителя иммитанса Е7-14.
Первая из них может быть оценена исходя из данных измерений нулевого сопротивления магазина. Полученный ряд данных характеризуется средним арифметическим значением и оценкой его СКО:
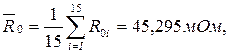
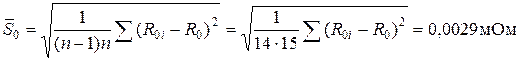
Сопротивление проводов постоянно присутствует в результатах измерений и по своей сути является систематической погрешностью, которая может быть исключена из результатов измерений путем введения поправки  , равной –45,295 мОм, т.к.
, равной –45,295 мОм, т.к. 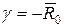 .
.
Доверительный интервал погрешности измерения сопротивления проводов, равный 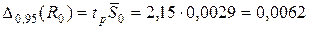 мОм при доверительной вероятности Р = 0,95, можно рассматривать двояко: как неисключительную систематическую погрешность и как составляющую случайной погрешности. В любом случае, как это будет видно далее, ее значение столь мало, что согласно критерию ничтожно малой погрешности ею можно пренебречь.
мОм при доверительной вероятности Р = 0,95, можно рассматривать двояко: как неисключительную систематическую погрешность и как составляющую случайной погрешности. В любом случае, как это будет видно далее, ее значение столь мало, что согласно критерию ничтожно малой погрешности ею можно пренебречь.
После введения поправки получается исправленный ряд значений сопротивления Rиi: 100,145; 100,065; 100,135; 100,085; 100,145; 100,125; 100,115; 100,095; 100,105; 100,115; 100,155; 100,135; 100,165; 100,075; 100,185 мОм.
Составляющая систематической погрешности, обусловленная основной погрешностью измерителя иммитанса Е7-14, рассчитывается согласно паспорту по формуле 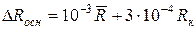 , а для нашего случая
, а для нашего случая
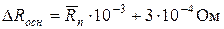 .
.
Здесь 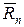 - среднее арифметическое значений ряда неисправленных показаний измерителя иммитанса, равное 145,418 мОм. Следовательно, систематическая погрешность, обусловленная основной погрешностью Е7-14
- среднее арифметическое значений ряда неисправленных показаний измерителя иммитанса, равное 145,418 мОм. Следовательно, систематическая погрешность, обусловленная основной погрешностью Е7-14
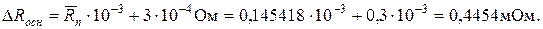
Систематическая погрешность, обусловленная дополнительной погрешностью средства измерений из-за влияния температуры (согласно паспорту) определяется по формуле
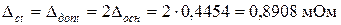 .
.
Дата добавления: 2014-12-22; просмотров: 23524;
