Плывучие породы (плывуны)
Различают псевдоплывуны и истинные плывуны. Псевдоплывуны – мелко – и среднезернистые пески без значительней примеси илистых и глинистых частиц. При откачке воды (искусственном понижении гидростатического уровня) они легко поддаются осушению и превращаются в плотные, достаточно устойчивые породы.
Истинные плывуны – мелкозернистый и пылеватый песок со значительной примесью органического и неорганического ила и глинистых частиц – содержат связанную воду за счет присутствия глинистых и коллоидных образований; часто обладают тиксотропными свойствами; при искусственном водопонижении практически не осушаются; вызывают большие трудности при пересечении их горными выработками (оплывают).
Подземные воды, насыщающие плывуны, оказывают гидростатическое давление на зерна породы, вызывая их взвешивание. Объемная масса (вес) водопроницаемой породы, залегающей ниже уровня подземных вод, определяется с учетом взвешивающего (по закону Архимеда) действия воды:
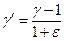 ,
,
где:
γ – удельная масса (вес) твердых частиц (скелета) породы;
1 – удельная масса (вес) воды;
ε – коэффициент пористости породы.
Если подземные воды находятся в движении, то к гидростатическому давлению добавляется гидродинамический напор, величина которого определяется перепадом давления (гидравлическим градиентом потока).
Плывучесть обводненных несвязных пород при их обнажении возникает вследствие того, что силы внутреннего трения и сцепления породы оказываются недостаточными для преодоления гидродинамического напора, создаваемого фильтрационным потоком воды, движущимся по направлению к обнаженной поверхности.
3.6. Задачи и примеры к разделу 3*
Задача 3.6.1.Определение значения действующего диаметра и коэффициента неоднородности сыпучей породы по графику гранулометрического состава
Условие задачи
Построить график гранулометрического состава и определить действующий диаметр и коэффициент неоднородности породы в следующих условиях:
- масса исходного материала (пробы) G = 10 кг;
- значения масс, оставшихся на ситах Gi (кг), указаны в табл. 1.
Таблица 1
| Диаметр отверстий сита, мм | Значения масс, оставшихся на ситах Gi, кг |
| G1 = 1,0 | |
| G2 = 1,0 | |
| G3 = 2,0 | |
| G4 = 3,0 | |
| G5 = 2,0 | |
| G6 = 0,5 | |
| 0,5 | G7 = 0,4 |
Наибольший диаметр куска – 60 мм
Решение
Гранулометрический состав (ГМС) характеризует весовое содержание в раздельнозернистой (сыпучей) породе частиц различной крупности в % от общего веса породы в абсолютно сухом состоянии.
Наиболее распространенным способом определения ГМС является ситовый анализ. Породу просеивают через установленные друг на друга сита с различными размерами отверстий. Затем взвешивают оставшиеся на ситах фракции с точностью до 0,01 г. После определения веса остатков на всех ситах и в поддоне вычисляют процентное содержание фракций в породе.
ГМС породы существенно влияет на ее водно-физические и механические свойства (пористость, сжимаемость, водопроницаемость, сопротивление сдвигу и др.).
1.Определение суммарной массы породы на ситах 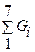 .
.
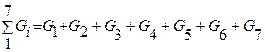 , кг
, кг
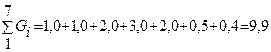 кг
кг
2.Определение массы породы крупностью менее 0,5 кг G8.
 , кг
, кг
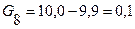 кг
кг
3.Определение относительной массы породы по классам крупности gi.
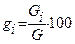 , %
, %
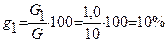
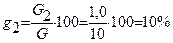
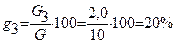
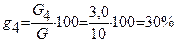
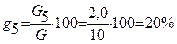
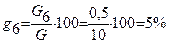
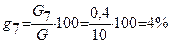
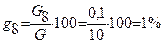
4.Построение графика гранулометрического состава (рис. 1).
По полученным данным составляем таблицу (табл. 2) и строим график гранулометрического состава (рис. 1).
Таблица 2
| № сита | Размер отверстий сит, мм | Класс крупности фракций, оставшихся на ситах, мм | Вес остатков на ситах | Суммарное содержание частиц соответствующего класса крупности | ||
| G, кг | g, % | класс крупности |  , % , %
| |||
| -60 +50 | 1,0 | -60 | ||||
| -50 +20 | 1,0 | -50 | ||||
| -20 +10 | 2,0 | -20 | ||||
| -10 +5 | 3,0 | -10 | ||||
| -5 +2 | 2,0 | -5 | ||||
| -2 +1 | 0,5 | -2 | 5 +5 = 10 | |||
| 0,5 | -1 +0,5 | 0,4 | -1 | 1+4 = 5 | ||
| 8 поддон | -0,5 | 0,1 | -0,5 | |||
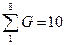 кг кг
| 
|
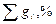
 d, мм
d, мм
Рис.1. График гранулометрического состава сыпучей породы
5.Определение действующего диаметра dl .
Действующим диаметром называется крупность частиц, соответствующая 10% их содержания в горной породе.
Из графика (рис. 1) находим  = 2 мм
= 2 мм
6.Определение коэффициента неоднородности КН.
Коэффициент неоднородности породы КН находится как отношение крупности частиц, соответствующей 60% их содержания в горной породе d60, к действующему диаметру dl.

Из графика (рис. 1) находим  = 10 мм
= 10 мм
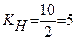
Задание для самостоятельного решения
Построить график гранулометрического состава и определить действующий диаметр и коэффициент неоднородности породы в следующих условиях:
- масса исходного материала (пробы) G = 10 кг;
- значения масс, оставшихся на ситах Gi (кг), указаны в табл. 3.
Таблица 3
| Диаметр отверстий сита, мм | Значения масс, оставшихся на ситах по вариантам, Gi, кг | ||
| 1 | 2 | 3 | |
| 1,5 | 1,3 | 1,2 | |
| 1,5 | 1,7 | 1,8 | |
| 1,5 | 1,5 | 1,7 | |
| 2,5 | 2,5 | 2,3 | |
| 2,0 | 1,5 | 1,3 | |
| 0,5 | 1,0 | 1,2 | |
| 0,5 | 0,3 | 0,4 | 0,4 |
| Наибольший диаметр куска, мм |
4. ОСОБЕННОСТИ ГОРНЫХ ПОРОД КАК *
СРЕДЫ
4.1. Минимальный размер образцов*
Методы механики сплошной среды (теория сопротивления материалов, упругости, пластичности и др.) основаны на рассмотрении состояния тела в бесконечно малом объеме. Таким образом, допускается возможность выделения в теле бесконечно малых объемов, обладающих всеми свойствами этого тела. Горные породы состоят из минеральных частиц либо связанных цементом, либо отделенных друг от друга. В связи с таким строением горных пород возникает вопрос: допустимо ли применять методы механики сплошной среды к горным породам? Строго говоря – нет. Практически – допустимо, но с определенными ограничениями. Применительно к горным породам расчет ведется не на бесконечно малый, а на элементарный объем, обладающий в достаточной мере свойствами всего объема породы (минимальный представительный объем). В связи с этим истинные напряжения в точке заменяются средними на так называемой элементарной площадке, которая представляет собой площадь сечения элементарного объема.
Размер элементарной площадки принимается из условия размещения на ней не менее 30 минеральных зерен породы. Как показывают расчеты, линейный размер элементарной площадки можно определить по формуле
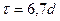 ,
,
где:d – средний размер составляющих породу зерен.
Ошибка (отклонение) подсчитанного среднего напряжения на элементарной площадке от действительного в точке определяется по формуле Ф. Ясинского
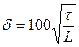 , (%)
, (%)
где:τ – размер элементарной площадки;
L – наименьший размер образца.
Приведенная формула позволяет определить минимальный размер образца породы в определении ее физико-механической характеристики:
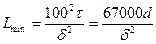 ,
,
где:  и τ – выражены в см;
и τ – выражены в см;
δ – допустимая ошибка, (%).
Уменьшение размеров образца целесообразно с точки зрения снижения трудоемкости его изготовления, а также размеров и мощности оборудования для испытания образцов.
4.2. Надежное число испытаний образцов*
Задачей механических испытаний является установление характеристик породы, определяющих ее поведение в тех или иных условиях напряженного состояния. Результаты испытаний являются величинами статистическими.
Надежность механических испытаний пород является мерой количественного соответствия определяемого показателя его назначению (использования показателя в расчетах при проектировании горных работ).
Математическое понятие надежности (обеспеченности) связано с величиной доверительной вероятности определения показателя (и коэффициента вариации этого показателя) по ограниченной выборке усредняемых статистических повторений единичных событий. При лабораторном испытании n образцов породы вариация определяемого показателя находит свое отражение в разбросе результатов испытания образцов:
х1, х2, х3, …хi, …xn.
Среднее по данной группе образцов значение показателя  , среднеквадратичный разброс σ и коэффициент вариации V определяются по формулам:
, среднеквадратичный разброс σ и коэффициент вариации V определяются по формулам:

Рассчитанное среднее значение 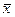 вследствие ограниченности числа испытанных образцов n будет отличаться от истинного среднего значения х0, которое могло бы быть определено лишь по результатам бесконечно большой группы образцов. Чем больше число испытанных образцов и чем ближе значения
вследствие ограниченности числа испытанных образцов n будет отличаться от истинного среднего значения х0, которое могло бы быть определено лишь по результатам бесконечно большой группы образцов. Чем больше число испытанных образцов и чем ближе значения 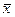 и х0, тем выше надежность полученного среднего значения показателя.
и х0, тем выше надежность полученного среднего значения показателя.
Минимальное надежное число образцов при испытании устанавливается по величине характерного (на основе предварительных испытаний) для данного типа пород коэффициента вариации данного показателя и допустимой ошибки результатов испытаний.
Расчет ведется по формуле:
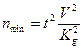 ,
,
где:t – нормированное отклонение (берется из таблицы в зависимости от принимаемой надежности испытаний);
V – коэффициент вариации показателя;
Kg – допустимая ошибка в определении показателя.
Для массовых испытаний горных пород принимается надежность в пределах 0,6–0,85, что соответствует t = 1,28÷1,44.
4.3. Задачи и примеры к разделу 4*
Задача 4.3.1.Определение представительного размера и числа образцов
Условие задачи
Из массивно-кристаллической породы изготовлено и испытано 5 образцов (n) диаметром d = 5 см и высотой H = 10 см. Крупность зерен породы и значения временного сопротивления образцов на одноосное сжатие приведены в табл. 1.
Проверить корректность выполненной работы при допустимой погрешности  = 15% и принятой надежности 0,85.
= 15% и принятой надежности 0,85.
Таблица 1
| Крупность зерен породыd, см | Временное сопротивление на одноосное сжатие образцов, Ri, МПа | ||||
| R1 | R2 | R3 | R4 | R5 | |
| 0,010 |
Решение
1.Определение минимально необходимого размера образца Lmin при 
Для установления характеристик породы, определяющих ее поведение в тех или иных условиях напряженного состояния, необходимо провести механические испытания образов данной породы. При этом для получения результатов, которые можно использовать в расчетах при проектировании горных работ, необходимо испытывать определенное количество образцов оптимального размера.
Для определения минимально необходимого размера образца применяют методы механики сплошной среды.
Теоретически к горным породам данные методы мы применить не можем, т. к. горные породы состоят из различных минеральных частиц (т.е. неоднородны).
Практически свойства горных пород определяются методами механики сплошной среды, но с некоторыми ограничениями.
Методы механики сплошной среды основаны на рассмотрении состояния тела в бесконечно малом объеме, т.е. выделенный из тела бесконечно малый объем обладает теми же свойствами, что и тело, из которого его выделили.
При определении свойств горных пород расчет ведется не на бесконечно малый объем, а на элементарный объем. Элементарный объем (минимальный представительный объем) – это объем, который обладает свойствами всего объема породы в достаточной мере. В связи с этим истинные напряжения в точке заменяются средними на так называемой элементарной площадке – площади сечения элементарного объема.
Размер элементарной площадки принимается из условия размещения на ней не менее 30 минеральных зерен породы.
Линейный размер элементарной площадки τ рассчитывается по формуле:
 , см
, см
| где | d | - | средний размер составляющих породу зерен, см. |
Ошибка в расчете среднего напряжения на элементарной площадке  определяется по формуле Ф. Ясинского:
определяется по формуле Ф. Ясинского:
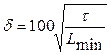 , %
, %
| е | Lmin | - | наименьший размер образца породы, см. |
Зная, что 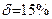 , найдем Lmin:
, найдем Lmin:
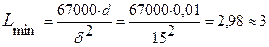 см
см
Диаметр образцов должен быть не меньше Lmin .
Имеем 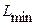 < d; 3 см < 5 см.
< d; 3 см < 5 см.
Следовательно, диаметр образцов принят правильно.
2.Определение минимально необходимого числа образцов nmin.
Результаты механических испытаний являются величинами статистическими. Мерой количественного соответствия определяемого показателя его назначению является надежность механических испытаний.
Математическое понятие надежности связано со следующими величинами:
- доверительной вероятностью;
- коэффициентом вариации.
Данные величины определяются по ограниченной выборке усредненных статистических повторений единичных событий 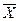 . Т.е. проводятся лабораторные испытания n образцов породы – Х1, Х2, …, Хn, затем по данной группе образцов рассчитывается среднее значение показателя
. Т.е. проводятся лабораторные испытания n образцов породы – Х1, Х2, …, Хn, затем по данной группе образцов рассчитывается среднее значение показателя 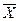 , по которому определяются доверительная вероятность и коэффициент вариации.
, по которому определяются доверительная вероятность и коэффициент вариации.
Рассчитанное среднее значение 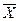 не будет равно истинному среднему значению, т.к. число испытанных образцов n ограничено. Определить истинное среднее значение можно было бы только по результатам испытаний бесконечно большой группы образцов. Таким образом, надежность испытаний увеличивается при увеличении количества образцов.
не будет равно истинному среднему значению, т.к. число испытанных образцов n ограничено. Определить истинное среднее значение можно было бы только по результатам испытаний бесконечно большой группы образцов. Таким образом, надежность испытаний увеличивается при увеличении количества образцов.
Минимальное надежное число образцов nmin – это число образцов, которого достаточно для получения результатов заданной надежности.
 ,
,
| где | t | - | нормированное отклонение; |
| VВ | - | коэффициент вариации показателя, %; | |
| KД | - | допустимая ошибка в определении показателя, %. |
Для массовых испытаний горных пород принимается надежность в пределах 0,8 – 0,85, что соответствует t = 1,28 – 1,44.
В нашем случае при надежности 0,85 t = 1,44.
Допустимая ошибка в определении показателя  .
.
Коэффициент вариации:  , %
, %
| где | 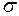
| - | среднее квадратичное отклонение (в данной задаче в МПа); |

| - | среднее арифметическое Ri, МПа. |
Среднее арифметическое значение показателя  по данной группе образцов рассчитывается по формуле:
по данной группе образцов рассчитывается по формуле:
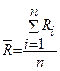 , МПа
, МПа
| где | Ri | - | значение временного сопротивления на одноосное сжатие i-го образца, МПа; |
| n | - | количество испытанных образцов. |

Среднее квадратичное отклонение σ:
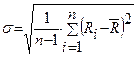 , (в данной задаче МПа)
, (в данной задаче МПа)
Расчет  приведен в табл. 2.
приведен в табл. 2.
Таблица 2
| № образца | Разрушающее
напряжение ,МПа ,МПа
| Отклонение от среднего
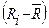 , МПа , МПа
| Квадрат отклонения от среднего
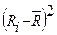 , МПа , МПа
|
| 8,6 | 73,96 | ||
| -9,4 | 88,36 | ||
| 36,6 | 1339,56 | ||
| -16,4 | 268,96 | ||
| -19,4 | 376,36 | ||
| Итого: | 2147,2 |

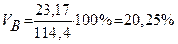
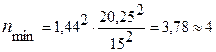 образца
образца
Количество испытаний n должно быть не меньше nmin.
Имеем  < n; 4 < 5.
< n; 4 < 5.
Следовательно, число образцов выбрано правильно.
Работа выполнена корректно. Результаты испытаний можно использовать с достаточной надежностью.
Задание для самостоятельного решения
Из массивно-кристаллической породы изготовлено и испытано 5 образцов (n) диаметром d = 5 см и высотой H = 10 см. Крупность зерен породы и значения временного сопротивления образцов на одноосное сжатие приведены в табл. 3.
Проверить корректность выполненной работы при допустимой погрешности  = 14% и принятой надежности 0,8 (t = 1,28).
= 14% и принятой надежности 0,8 (t = 1,28).
Таблица 3
| Вариант | Крупность зерен породы d, см | Временное сопротивление на одноосное сжатие образцов Ri, МПа | ||||
| R1 | R2 | R3 | R4 | R5 | ||
| 0,013 | ||||||
| 0,014 | ||||||
| 0,013 |
Дата добавления: 2014-12-21; просмотров: 1251;
