Напряженное состояние горных пород и устойчивость горных выработок
5.1. .Основные понятия*
Пусть твердое тело U (рис. 12.а) находится в равновесии под действием внешних сил Р, Р1, Р2, Р3, Р4.В сечении внешние силы уравновешиваются внутренними силами (напряжениями).
Рассмотрим небольшую площадку в сечении S (рис. 12.б) величиной S около точки А. Пусть на нее действует сила  . Тогда среднее напряжение на площадке
. Тогда среднее напряжение на площадке 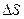 составит:
составит:
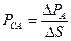 .
.

Рис. 12. Схема напряженного состояния твердого тела:
а – силы Р, Р1, Р2, Р3, Р4 находятся в равновесии;
б – напряжение на площадке 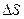
Истинное напряжение в точке А составит:
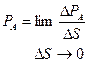 .
.
Напряжение в точке А можно разложить на две составляющие:
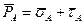 ,
,
где
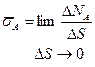 – нормальное напряжение;
– нормальное напряжение;
 – касательное напряжение.
– касательное напряжение.
В теории упругости доказывается, что для любой точки тела, при любом напряженном состоянии имеются три взаимно перпендикулярные плоскости, на которых касательные напряжения отсутствуют. Нормальные напряжения на этих площадках называются главными нормальными напряжениями и обозначаются σ1, σ2, σ3, причем σ1> σ2> σ3, Нормали к указанным площадкам называются главными осями напряжений и обозначаются соответственно 1, 2, 3. Касательные напряжения на площадках, делящих пополам угол между главными осями, называются главными касательными напряжениями и обозначаются (рис. 13)
τ12 = τ21; τ23 = τ32; τ31 = τ13.
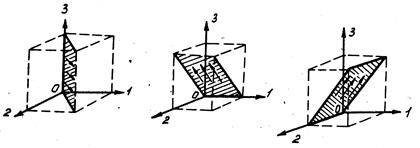
Рис.13. Площадки главных касательных напряжений
Величины главных касательных напряжений составляют
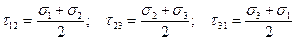 .
.
На площадках главных касательных напряжений нормальные напряжения составляют
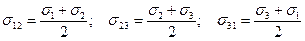 .
.
Дата добавления: 2014-12-21; просмотров: 858;
