Напряжение в породном массиве

Рассмотрим напряженное состояние кубика породного массива, расположенного на глубине H = Z от поверхности (рис.14). Обозначим вертикальное напряжение σ_z и горизонтальные – σ_x и σ_y. Тогда относительные деформации кубика можно выразить в виде

где:

Е – модуль упругости массива в простом напряженном состоянии.

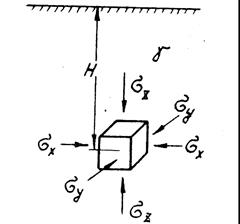
Рис. 14. Схема напряженного состояния породного массива

В 1952 г. Терцаги и Рихарт внесли предложение принять ε_х = ε_у = 0, откуда следует:

.

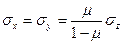Эта зависимость, по-видимому, имеет место в крепких горных породах при относительно небольших напряжениях.

В 1912 г. Гейм предложил считать 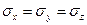на том основании, что с течением времени напряженное состояние пород выравнивается. Предложение Гейма, по-видимому, можно принять для пластичных пород, особенно на глубинах более 1 км.

На рис.15 приведена зависимость вертикального напряжения в горном массиве σ_z от глубины Z на основе натурных наблюдений.

Эта зависимость выражается формулой:

,

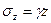где

γ – средневзвешенный объемный вес пород;

z – глубина от поверхности.

На рис. 16 приведена зависимость от глубины отношения средних горизонтальных напряжений к вертикальным. Это отношение укладывается в область, ограниченную кривыми :

.

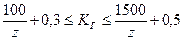Из графика рис.16 видно, что на малых глубинах (до 500 м) горизонтальные напряжения значительно выше вертикальных. На глубинах 1 км и более значения горизонтальных и вертикальных напряжений выравниваются. Все это говорит о важности натурных замеров напряженного состояния горных пород при решении горных задач.

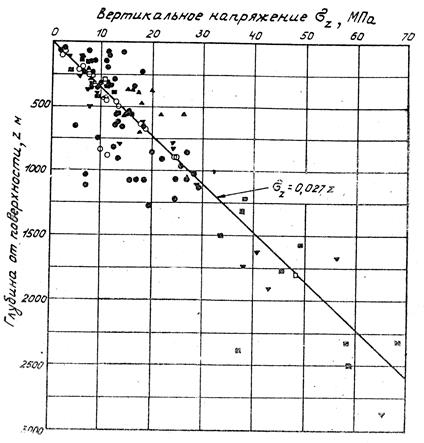
Рис. 15. Зависимость вертикального напряжения от глубины:

● Австралия, ▼ Канада, ▲ США, ○ Скандинавские страны,

■ Южная Африка, □ другие районы

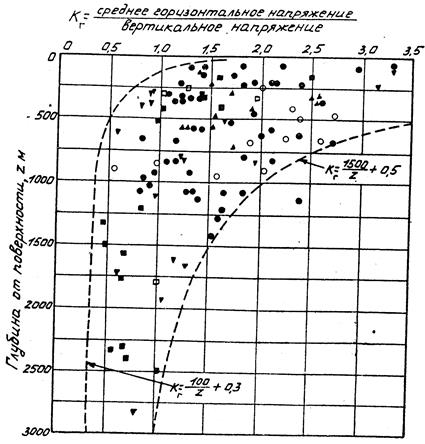
Рис. 16. Зависимость отношения

средних горизонтальных напряжения к вертикальным от глубины:

● Австралия, ▼ Канада, ▲ США, ○ Скандинавские страны,

■ Южная Африка, □ другие районы