Симметричная разность множеств
Множество всех элементов, принадлежащих либо только множеству А, либо только множеству В называется симметричной разностью множеств А и В Операция симметричной разности обозначается знаком «Å».
На рисунке 4.5. изображено множество С, являющееся симметричной разностью множеств А и В.
С=АÅB : (хÎAÅB)«((хÎA)&(хÏB))V((xÏA)&(xÎB))
Пример: {1,2,3}Å{2,3,4}={1,4}
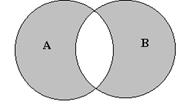
Рис. 4.5 С=АÅB
3.3. Включения. Подмножество. Пустое множество
Множество А называется подмножеством множества В, если любой элемент из А является элементом множества В. Факт, что А является подмножеством В записывается с помощью « Ì » – знак включения.
Запись A Ì B можно прочитать как «А - подмножество В» или «В включает А» или «В содержит А».
Понятие подмножества возникает каждый раз, когда приходится рассматривать некоторое множество не самостоятельно, а как часть другого, более широкого множества. Например, если рассмотреть среднюю школу, то множество учеников десятого класса этой школы является подмножеством во множестве всех учеников этой школы. Или, например, множество треугольников является подмножеством всех геометрических фигур.
Введем понятие строгого включения множества (символ «Í»).
Множество A строго включается во множество В (А является строгим подмножеством В), если любой элемент из А является элементом множества В, и во множестве В содержится по крайней мере один элемент, не принадлежащий А. На рис. 4.6 изображено строгое включение множества А в В.
Рис.4.6.
Введем понятие множества всех подмножеств в некотором множестве Х, по-другому называемом множеством-степенью:
P(Х)={U½U Ì C}.
Из основных принципов теории множеств следует существование единственного множества, не имеющего элементов – “Æ” – пустое множество.
Æ={ }
Пустое множество по определению является подмножеством любого множества, причем строгим.
Пример. Дано множество A={a,b,c}. Построить P(А) – множество-степень для множества А.
P (A)={Æ, {a}, {b}, {c}, {a, b}, {b, c}, {a,c}, {a,b,c}}
Если некоторое множество содержит n элементов, то его степень множества будет содержать 2n элементов.
3.4. Универсум. Дополнение.
Обычно все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого фиксированного множества U. Например, множества рыб, моллюсков, планктона, крабообразных являются подмножествами объемлющего их множества фауны. Это общее множество назовем универсумом.
Универсумили универсальное множество (U) – множество, которое состоит из всех элементов, а также подмножеств множества исследуемых объектов исследуемой области, т.е. универсум должен удовлетворять следующим условиям:
- если А Î U, то А Í U;
- если А Î U, то P(А) Î U, где P(А) – множество всех подмножеств множества А;
- если А Î U и В Î U, то и {A, B}Î U ;
- если F=(Fi)iÎI, где Fi Î U и I Î U, то ÈFi Î U.
В системе диаграмм Эйлера, универсальное множество U изображается в виде прямоугольника, а множества, являющиеся его подмножествами, - в виде кругов, находящихся внутри прямоугольника U.
Множество Ā= U \ A называют дополнением множества А.
На рис. 4.7 приведено изображение универсального подмножества, множества А и дополнения множества Ā.

Рис.4.7
Анализируя рис. 4.7. можно сделать следующие выводы:
AÈU=U
AÇU=A
Ā ÈA=U
Ā ÇA=Æ
_____
(Ā)=A
AÈÆ=A
AÇÆ=Æ
3.5. Свойства операций над множествами
Приоритет операций над множествами определяется следующим образом: наивысший приоритет имеет дополнение ( ¯ ), далее в порядке убывания приоритета следуют операция Ç, далее - È. Порядок выполнения операций может быть изменен скобками.
Алгебра множеств представляет собой совокупность тождеств, справедливых независимо от того, какие конкретные множества и подмножества, входящие в равенства, обозначены буквами и независимо от того, какое универсальное множество имеется в виду.
 |
Далее приведены основные тождества алгебры множеств:
Законы де Моргана:
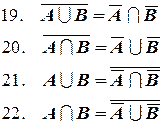
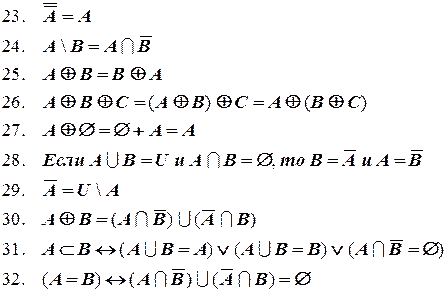
Дата добавления: 2019-10-16; просмотров: 1736;
