Формулы алгебры-логики
Формулой алгебры-логики называется выражение, состоящее из логических постоянных, логических переменных, знаков логических операций и круглых скобок, изменяющих порядок выполнения операций, относительного стандартного.
Формулы соответствуют сложным или составным высказываниям. Для определения истинности или ложности высказывания, необходимо вычислить истинностное значение формулы. Для вычисления значения формулы должны быть известны входящие в нее переменные. Порядок выполнения операций следующий (в скобках указан приоритет выполнения операций): ù (1), & (2), V (3), ® (4), « (5), Å (5). Операции одного старшинства выполняются слева направо. Порядок выполнения операций может быть измене с помощью скобок. Операции в скобках имеют более высокий приоритет.
Пример: Если «Пираты» или «Щенки» проиграют, а «Великаны» выиграют, то «Увертыши» потеряют первое место, и, кроме того, я проиграю пари.
Формализуем данное высказывание.
P - «Пираты» проиграют;
D - «Щенки» проиграют;
Q - «Великаны» выиграют;
G - «Увертыши» потеряют первое место;
C - я проиграю пари.
Составное высказывание будет выглядеть следующим образом:
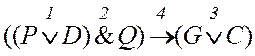
1.2. Таблицы истинности в алгебре логики.
Для того чтобы определить значение формулы при различных комбинациях значений входящих в нее переменных, используют таблицы истинности.
Таблица истинности состоит из следующих частей:
- в левой части таблицы столбцы соответствуют логическим переменным, входящим в формулу (исходные данные);
- далее следуют столбцы, отображающие результаты выполнения промежуточных операций в порядке их приоритетности (промежуточные результаты);
- крайний правый столбец отображает конечные значения формулы (результирующий столбец).
Каждая строка таблицы истинности заполняется определенным набором истинностных значений переменных и получаемым на этом наборе истинностным значением формулы. Все строки совокупности представляют полный набор возможных сочетаний истинностных значений переменных. Если в формулу входит N переменных, то всего в таблице должно быть 2N строк.
Таблицы истинности используются в качестве формального определения операций (см. табл. 1.2. – 1. 7).
Таблица 1.2.
Операция отрицания
| Х | ù C |
| Л | И |
| И | Л |
Таблица 1.3.
Дата добавления: 2019-10-16; просмотров: 692;
