Логические операции
| Операция | Связка | Обо-значение |
| Отрицание | НЕ<высказывание А> | ù А ~А Ā |
| Конъюнкция | <высказывание А> И <высказывание B> | A&B A L B |
| Дизъюнкция | <высказывание А> ИЛИ <высказывание B> | АV B |
| Импликация | ЕСЛИ<высказывание А>,ТО<высказывание B> | |
| Эквиваленция | <высказывание А> ТОГДА И ТОЛЬКО ТОГДА, КОГДА<высказывание В> | А«В |
| Антиэквиваленция | ИЛИ<высказывание А>, ИЛИ<высказывание В> | АÅВ |
Рассмотрим сущность этих операций.
² Операция отрицания
Отрицанием высказывания А называется новое высказывание ùА, которое является истинным, если высказывание А ложно, и ложным, если высказывание А – истинно.
Проанализируем высказывание « 3- нечетное число».
Как записать это высказывание, используя язык формальной логики? Для начала перефразируем это высказывание: НЕ «3 есть четное число».Элементарным высказыванием является фраза«3 есть четное число»,и его обозначим символом А. Т.о., на языке формальной логики заданная фраза будет записана как ùА.
² Операция конъюнкции
Конъюнкцией двух высказываний А и В называется новое высказывание А & В, которое считается истинным, если оба входящие в нее высказывания имеют значение «истина», и ложным, если хотя бы одно из высказываний имеет значение ложь.
Союзы «И», «А», «НО», используемые при формализации конъюнкции, являются синонимами.
Рассмотрим следующее составное высказывание:
4 – четное число, а 6 – простое число.
Элементарное высказывание «4 – четное число», обозначим буквой Х, а высказывание «6 – простое число» - буквой Y. Высказывание «4 – четное число» имеет значение «истина», а высказывание «6 – простое число» имеет значение «ложь». Результирующее высказывание будет на языке формальной логики выглядеть следующим образом:
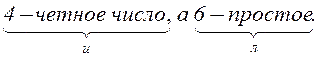
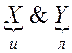
² Операция дизъюнкции
Дизъюнкцией двух высказываний Х и Y называется новое высказывание Х Ú Y, которое считается истинным, если хотя бы одно из высказываний имеет значение «истина», и ложным, если оба входящие в нее высказывания имеют значение «ложь».
Рассмотрим пример высказывания, содержащий операцию дизъюнкции.
2 – простое число, или 3 – нечетное число.
Обозначим буквой Р высказывание «2 – простое число», а буквой Q – высказывание – «3 – нечетное число». Результирующее высказывание будет следующее:
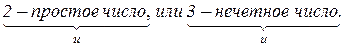
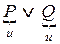
² Операция импликации
Составное высказывание, состоящее из двух высказываний Х и Y, между которыми стоит знак операции импликации (следования) - «®», называется импликацией.
Высказывание, стоящее слева от «®» - антецедент, справа - консеквент.
Импликация имеет значение «ложь» только в том случае, если антецедент - истина, а консеквент - ложь.
Импликация Х ® Y читается следующим образом: «если Х, то Y», «из Х следует Y».
Употребление слов «если …, то …»в алгебре логики отличается от употребления их в обыденной речи, где, как правило, считается, что если высказывание Х ложно, то высказывание «если Х, то Y» вообще не имеет смысла. Импликация выражает соотношение причины и следствия таким образом, что Х всегда является достаточным основанием для того, чтобы наступило Y. Но для наступления Y само по себе Х не нужно, поскольку Y может наступить также в силу действия другой причины, т.е. Х для Y не является необходимым основанием.
Т.о., возможно построение таких конструкций, в которых основание и следствие по содержанию никак не связаны друг с другом (например, «Если управление предприятием нерационально, то февраль – морозный.»). Логическое значение импликации от этого не меняется.
Пример: Если 3 – нечетное число, то 3 не делится на 2.
Обозначим высказывание «3 – нечетное число» буквой P, а высказывание «3 не делится на 2» буквой Q. Составное высказывание в алгебре логики будет выглядеть следующим образом:
P ® Q
и и
Синонимы P ® Q:
P влечет за собой Q.
Дата добавления: 2019-10-16; просмотров: 923;
