Таблицы смертности и страховые вероятности
Для осуществления актуарных расчетов, в том числе расчетов стоимости страховых аннуитетов необходимы исходные данные, характеризующие совокупность по полу и возрасту, а также системы нормативных и демографических показателей, отражающих статистические закономерности дожития до того или иного возраста. Последние содержаться в таблицах смертности.
Таблица смертности представляет собой числовую модель процесса вымирания по возрастам некоторой абстрактной совокупности людей. Такая таблица показывает, как последовательно с увеличением возраста уменьшается эта совокупность, достигая до нуля сразу после предельного возраста w. Она является обобщением данных демографической статистики за некоторый период времени.
Основной показатель таблицы смертности – число людей lx в возрасте равно X лет, оставшихся в живых из первоначальной совокупности l0 обычно равной 100 тысяч человек. Заметим, что и начальный возраст и первоначальное количество людей в таблице могут быть любыми – выбор того или иного начального возраста не влияет на результаты актуарных расчетов. Для актуарных расчетов применяют полные таблицы смертности, в которых возраст показан с интервалом один год.
Величины lx (кроме l0) определяется различным путем на основе заданных вероятностей смертности (gx), или что реже, количество умерших (dx). В современных таблицах смертности исходным показателем обычно служит вероятность смертности, то есть доля умерших в возрасте от x до х+1 лет из числа доживших до возраста х лет. Указанные вероятности получают на основе данных статистики населения с последующим их усреднением и сглаживанием.
Помимо показателей lx таблица смертности содержит число умерших за год в каждой возрастной группе (dx). Никакие иные факторы выбытия, кроме повозрастных вероятностей умереть, при разработке таблицы во внимание не принимается.
В качестве иллюстрации приведем фрагмент таблицы смертности для мужчин, в которой начальный возраст – 18 лет.
Таблица 4.1 Фрагмент таблицы смертности
| Х | lx | gx | dx |
| 100 000 | 0,00149 | ||
| 99 851 | 0,00173 | ||
| 99 678 | 0,00196 | ||
| … | |||
| 96 991 | 0,00381 | ||
| … | |||
| 94 951 | 0,00487 | ||
| … | |||
| 92 327 | 0,00708 | ||
| … | |||
| 83 640 | 0,01409 | ||
| … | |||
| 68 505 | 0,02871 | ||
| … | |||
| 45 654 | 0,05691 | ||
| … | |||
| 19 760 | 0,11672 |
Показанные в таблице величины lx и dx c сами по себе не имеют смысла. Они приобретают его лишь при сравнении в рамках таблицы смертности.
Показатели таблицы смертности связанные очевидными соотношениями.
Lx+1=lx-dx; dx=lx*gx;
gx=l-px=l- lx+1/ lx= dx/ lx .
Таблицы смертности, фрагмент которой приведен выше, является минимальной по набору показателей. Она достаточна для простых видов личного страхования – страхования на дожитие и страхование жизни. На практике применяют полные таблицы. В частности, в групповом, пенсионном и медицинском страховании применяют таблицы выбытия, в которой помимо смертности учитываются и другие причины сокращения числа участников страхования.
Страховые вероятности. На основе данных таблицы смертности можно получить систему вероятности дожития, необходимую для расчета соответствующих страховых показателей. Рассмотрим наиболее важные из таких вероятностей.
Вероятность прожить от возраста х до х+n: nPx= lx+n/ lx
Вероятность прожить еще один год после возраста х лет:
Px= l – gx=l - dx/ lx = lx+1/ lx
Пример: Вероятность мужчине в возрасте 30 лет прожить еще 10 лет составит:
10p30= l40/ l30=92 327/ 96 991 = 0,95191
По данным таблицы смертности находят вероятности смерти в определенных возрастах. Например, вероятность умереть в возрасте от х до х+n:
ngx =l – npx = (lx – lx+n)/lx= 1/lx* 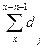
Пример: Вероятность для мужчины в возрасте 30 лет умереть в течение 10 следующих лет определяется как
10g30= 1- 10p30 = 1- 0,95191=0,04809
Вероятность умереть через m лет (на протяжении года m+1) для лица в возрасте х лет составит:
m|gx=mpx*gx+m=(lx+m/lx)*(dx+m/lx+m)=dx+m/lx
В свою очередь вероятность для лица в возрасте х лет умереть в возрастном интервале от х+m до x+m+n лет определим следующим путем:
m|ngx=(lx+m-lx+m+n)/lx=(lx+m/lx)*(lx+m-lx+m+n/lx+m)
Из последнего выражения вытекает, что
m|ngx=mpx*ngx+m
Искомая вероятность равна произведению вероятности дожить до возраста х+m лет и вероятности умереть в следующие n лет.
Пример:Найдем для мужчины в возрасте 30 лет вероятность умереть в течение 2 лет после достижения им 33 лет. Находим
3|2g30=(l33-l35)/l30=(95821-94951)/96991=0,00897
В некоторых актуарных расчетах (например, в пенсионном страховании) необходимы вероятности дожития супружеских пар. Эти вероятности также рассчитываются по таблицам смертности. Пусть речь идет о супругах в возрасте х и y лет и необходимо оценить вероятности прожить еще n лет для каждого из них. Обозначим эти вероятности как npx; npy. Определим их следующим образом:
npx= lx+n/lx; npy= ly+n/ly,
где lx, ly – числа доживших до соответствующих возрастов (берутся из таблиц смертности для мужчин и женщин). В свою очередь вероятности умереть для каждого из супругов составят:
ngx=1-npx; ngy=1-npy;
Рассчитаем еще две вероятности. Однако предварительно примем две рабочие гипотезы:
- оба супруга достигают возрастов х и y в один день;
- смерть одного супруга – страховое событие, независимое от смерти другого супруга.
Вероятность прожить супругам вместе еще n лет (вероятность «сохранения» супружеской пары) рассчитывается как произведение вероятностей двух независимых событий:
npxy= npx* npy= (lx+n/lx)*(ly+n/ly)= (lx+n* ly+n)/lx*ly
В актуарной практике фигурирующие в формуле произведения чисел доживших принято обозначить следующим образом
lx*ly=lxy и lx+n*ly+n=lxy+n
от сюда следует:
npxy=lxy+n/lxy
Найдем теперь вероятность того, что супруг (заключивший договор страхования в возрасте х лет, когда его супруге было y лет) не доживет до х+n лет. Искомая вероятность (обозначим ее как npx|y) равна произведению вероятностей:
npx|y= ngx* npy=(1- npx) npy= npy- npx* npy=(ly+n/ly)- (lxy+n/lxy)
Пример: пусть возраст супругов 50 и 45 лет. По таблицам смертности находим:
для мужчин l50=83640, l55=77007,
для женщин l45=96261, l50=94348.
Вероятность того, что оба супруга проживут следующие 5 лет, составит:
5p50;45=5p50*5p45=77007/83640*94348/96261=0,9024.
Вероятность того, что супруг не проживет 5 лет, а супруга проживет:
5p50;45=(1-5p50)*5p45=(1-0,9207)*0,98013=0,007772
Дата добавления: 2019-10-16; просмотров: 576;
