Тождества, связывающие накопления и аннуитеты
Функции составных платежей широко используются в финансовых расчетах, связанных с платежами, распределенными во времени. Важную роль при финансовых расчетах играют тождества, которые устанавливают часто используемые взаимоотношения между функциями составных платежей s 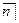 i и a
i и a 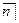 i
i
Воспользуемся равенством S=A(1+i)n.
Подставляя в это равенство значения Sи Aпо формулам (4.1) и (4.3) и сокращая обе части равенства на R , получим
sn┐i=(1+i)nan┐i (4.11)
Эта формула и определяет первое тождество, связывающее рассматриваемые функции.
Далее, из определения
sn┐i=((1+i)n-1)/i
следует, что
1+i sn┐i=(1+i)n
Поделив это равенство на (4.11), мы получим второе тождество
1/sn┐i+i=1/an┐i (4.12)
Оба тождества (4.11) и (4.12) справедливы для любых значений параметров nи i.В дополнение к только что полученным тождествам можно добавить и ряд других важных тождеств. Некоторые из них предлагается получить в порядке выполнения нижеследующих упражнений. Важность этих тождеств можно оценить тогда, когда при расчетах необходимо определять значения функций составных платежей для таких n, которые лежат за пределами имеющихся таблиц.
Пример 7. При приобретении дома необходимо заплатить 20 млн. руб. В день покупки и выплачивать 750 тыс. руб. ежемесячно в течение следующих 20 лет. Если деньги стоят j12 = 6% , какова стоимость дома на день покупки ?
РЕШЕНИЕ Поместим исходные данные на временную диаграмму
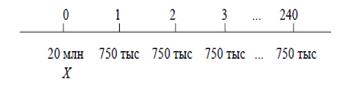
ΩΩΩ
Дата добавления: 2019-10-16; просмотров: 565;
