Отсроченные аннуитеты

Когда срок аннуитета устанавливается, начиная с некоторой даты в будущем относительно даты заключения сделки, аннуитет называется отсроченным аннуитетом. Обычно анализируют отсроченные аннуитеты как обыкновенные аннуитеты, поэтому в последующем слово «обыкновенные» для краткости будем опускать.

Продолжительность времени от даты заключения сделки до начала срока аннуитета, то есть до начала первого интервала платежа, называется периодом отсрочки. Таким образом, аннуитет, состоящий из полугодовых платежей, первый из которых делается через 4 года, квалифицировался бы как отсроченный аннуитет с периодом отсрочки 3,5 года.

Для определения настоящей стоимости отсроченного аннуитета не требуется никаких новых методов. Как обычно, составляется уравнение эквивалентности с удобной датой сравнения и из него находится текущая стоимость. Поясним это на примере.

Пример 6. Компания получила определенную сумму, которую она будет возмещать, выплачивая по 50 млн. руб. в месяц, первая выплата должна быть, сделана через 2 года, а последняя - через 5 лет от даты заключения сделки. Какую сумму получит компания в день заключения сделки при норме процента 6% , m = 12?

РЕШЕНИЕ Обозначим через A настоящую стоимость платежей и поместим исходные данные задачи на временную диаграмму

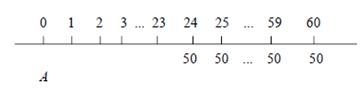
Способ 1. Первая выплата попадает на конец 24-го месяца, а последняя должна быть сделана в конце 60-го месяца, так что всего состоится 37 выплат. Поэтому эти платежи можно рассматривать как обыкновенный аннуитет с 37-ью платежами, отсроченными на 23 интервала платежа.

Выпишем уравнение эквивалентности на дату сравнения в конце 23-го месяца.

A(1,005)²³=50a₃₇┐_0,005млн. руб.

Умножая это равенство на (1,005^{) -23}, получим

A=(1,005)^-2350a₃₇┐_0,005 млн. руб.=0,891621650×33,70250372=1502,49 млн. руб.

Способ 2. Этот способ не очевидный и дает пример, когда небольшая изобретательность позволяет упростить вычисления. Поместим на диаграмму дополнительные платежи по 50 млн. руб. в концах первых 23-ех месяцев в обеих строках. Тогда диаграмма приобретет вид

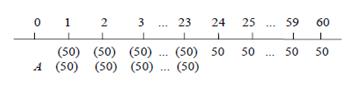
Поскольку дополнительные платежи будут одинаково входить в обе части уравнения эквивалентности, их присутствие не должно влиять на правильность результата. В правой части будет стоять стоимость аннуитета с 60-ью платежами, а к левой части добавится аннуитет с 23-мя платежами. Уравнение эквивалентности с датой сравнения в день заключения сделки в этом случае имеет вид

A+50a₂₃┐_0,005=50a₆₀┐_0,005 млн. руб.

Подставляя сюда соответствующие значения a 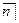_i из таблицы и выражая А, получим

A=50(a₆₀┐_0,005-a₂₃┐_0,005) млн. руб.=50(51,72556075-21,67568055)=1502,49 млн. руб.

Способ 1 является более естественным, но при наличии таблиц Способ 2 является более простым.

Если два способа, описанные в примере, применяются при расчете A для аннуитета с nплатежами по Rруб. каждый, отсроченного на kпериодов, и с нормой процента i за период, тогда общая формула будет:

Для способa 1 A=(1+i)^-kRa_n┐_i (4.8)

Для способа 2 A=R(a_n+k┐_i-a_k┐_i) (4.9)

Так как значения A для обоих методов должны быть одинаковы, приравнивая правые части равенств (4.8) и (4.9), мы получим полезное тождество

a_n+k┐_i-a_k┐_i=(1+i)^-ka_n┐_i (4.10)

Здесь следует заметить, что полезно освоить методы получения результатов, а не запоминать полученные формулы. Всегда нужно точно представлять исходные данные на временной диаграмме, правильно определяя количество платежей и период отсрочки.