Эквивалентные серии платежей

Одной из наиболее важных проблем в математике финансов является замена данной серии платежей или других обязательств на эквивалентную серию. Например, холодильник стоит 3 тыс. ден. ед. наличными. Однако его можно купить при помощи эквивалентной серии небольших ежемесячных платежей.

Выше рассмотрена датированная сумма серии платежей или обязательств. При этом было видно, что сумма серии зависела от используемой нормы процента и даты, на которую вычислялась сумма. На основе правила эквивалентности для таких серий можно сформулировать следующее утверждение: при данной норме сложного процента две серии платежей являются эквивалентными, если датированные суммы этих серий на любую общую дату являются равными. Таким образом, если стоимость холодильника равна 3 тыс. ден. ед., любая серия платежей, использованная при его покупке должна иметь стоимость на настоящий момент (текущую стоимость) 3 тыс. ден. ед. Равенство, устанавливающее, что датированные суммы двух серий на общую дату равны, называется уравнением эквивалентности или равенством стоимостей. Дата, используемая в этом равенстве, называется датой сравнения. Из свойства 1 следует, что в качестве даты сравнения может быть использована любая дата.

Использование уравнений эквивалентности показывает, что они связывают величины трех типов: суммы погашения, даты погашения и нормы процентов. До сих пор мы использовали уравнения эквивалентности только для определения неизвестных значений сумм погашения. Вместе с тем на практике уравнения эквивалентности используются также для определения и других составляющих: даты погашения или нормы процента. Хотя техника использования уравнений в этих случаях остается прежней, имеются некоторые особенности в деталях. Рассмотрим это на примере.

Пример 1. 100 тыс. руб. погашается через 5 лет и 200 тыс. руб. погашается через 10 лет. Если деньги стоят 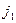= 4% . Через сколько лет оба платежа эквивалентно заменит выплата а) 250 тыс. руб.; b) 300 тыс.руб.?

Решение. а) Пусть п обозначает искомый временной интервал для 250 тыс. руб. Построим временную диаграмму:

Так как относительное положение п неизвестно, обычно предпочтительнее выбирать в качестве даты сравнения настоящее время. Преобразовывая все суммы к настоящему времени и составляя уравнение эквивалентности, получим равенство:

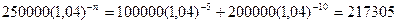
Разрешая теперь это равенство относительно п , находим, что п = 3,578 лет, то есть примерно 3 года 6 месяцев и 28 дней.

b) Процедура вычислений точно такая же, как и в случае а). Уравнение эквивалентности получается следующим:

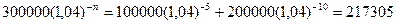
и разрешая его относительно п получим п = 8,226 лет или приблизительно 8 лет, 2 месяца и 21 день.

Когда серия обязательств заменяется единственным обязательством с суммой погашения, равной сумме сумм погашения всех обязательств серии, время выполнения этого обязательства при эквивалентной замене называется средней датой погашения или датой эквивалентности.

При объединении обязательств можно применить и учетные ставки (d). В этом случае при условии, что все сроки выплат пролонгируются, т.е. n₀ > n_j, находим сумму наращенных процентов по учетной ставке платежей:

S₀ =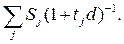

В общем случае имеем:

S₀ =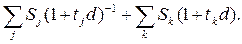

Консолидацию платежей можно осуществить на основе сложных ставок для общего случая (n₁ < n₀ < n_m):

S₀ =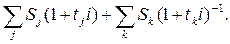

Если при объединении платежей задана величина консолидированного платежа S₀, то возникает проблема определения его срока n₀. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид:

S₀ (1 + n₀i)^-1 =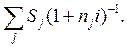

Отсюда

n₀ =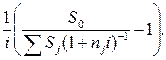

При консолидации платежей на основе сложных процентных ставок уравнение эквивалентности выглядит следующим образом:

S₀ (1 + i)^-n0 =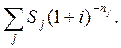

Для упрощения дальнейшей записи примем:

Q =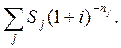

После чего находим:

n₀ =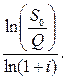

Если приведение платежа осуществляется на некоторую начальную дату, то получим следующие уравнения эквивалентности в общем виде:

- при использовании простых процентов

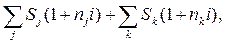
- при использовании сложных процентов

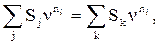
где S_j и n_j – параметры заменяемых платежей;

S_k и n_k – параметры заменяющих платежей.

Часто при расчетах, проводимых по различным финансовым операциям, возникает необходимость определения эквивалентных процентных ставок.

Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.

Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.

Для нахождения эквивалентных процентных ставок также используется уравнение эквивалентности. Выбирается величина, которую можно считать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.

Формулы эквивалентности ставок во всех случаях получаются исходя из равенства взятых попарно множителей наращения.

Пример 2. Определим соотношение эквивалентности между простой и сложной ставками наращения. Для этого приравняем друг к другу соответствующие множители наращения:

(1 + ni_s) = (1 + i)ⁿ,

где i_s и i – ставки простых и сложных процентов.

Приведенное равенство предполагает, что начальные и наращенные суммы при применении двух видов ставок идентичны.

Решение дает следующие отношения эквивалентных ставок:

i_s =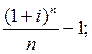

i =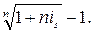

Аналогичные формулы могут быть получены для всех видов процентных ставок.

Из выше изложенного можно сделать следующие выводы:

-важным и полезным свойством эквивалентных датированных сумм является свойство 1: при данной норме сложного процента если А эквивалентно В и В эквивалентно С, то А эквивалентно С;

-для различных датированных сумм одной и той же серии справедливо следующее свойство 2: датированные суммы одной и той же серии, определенные для различных дат, являются эквивалентными.

-равенство, устанавливающее, что датированные суммы двух серий на общую дату равны, называется уравнением эквивалентности или равенством стоимостей. Дата, используемая в этом равенстве, называется датой сравнения;

-когда серия обязательств заменяется единственным обязательством с суммой погашения, равной сумме сумм погашения всех обязательств серии, время выполнения этого обязательства при эквивалентной замене называется средней датой погашения илидатой эквивалентности.

В практической деятельности часто возникает необходимость изменения условий ранее заключенного контракта – объединение нескольких платежей или замене единовременного платежа рядом последовательных платежей. Естественно, что в таких условиях ни один из участников финансовой операции не должен терпеть убыток, вызванный изменением финансовых условий.

Решение подобных задач сводится к построению уравнения эквивалентности, в котором сумма заменяемых платежей, приведенная к какому-то одному моменту времени, приравнена к сумме платежей по новому обязательству, приведенному к тому же моменту времени.

Тестовые задания

3013214. Две финансовые схемы можно считать эквивалентными, если они приводят:

1. К финансовым результатам, предусмотренным договором;

2. К разным финансовым результатам;

3. К одной и той же дате расчета;

4. К одному и тому же финансовому результату.

3022134. Датированной суммой называется:

1. Сумма платежа с дисконтом;

2. Сумма платежа по определенной ставке;

3. Сумма платежа вместе с датой погашения;

4. Сумма платежа, обусловленная нормой процента.

3031234. Датированные суммы сравниваются по следующему правилу эквивалентности: сумма Р, полагающаяся на данную дату, эквивалентна при данной норме сложного процента i сумме S , полагающейся нап периодов конверсии позже, если является справедливым хотя бы одно из следующих равенств:

1. S=P(1+i)^-n или P=S(1+i)^-n ;

2.S=P(1+i)ⁿ или P=S(1+i)^-n ;

3. S=P(1+i)^-n или P=S(1+i)ⁿ ;

4. S=P(1+i)ⁿ или P=S(1+i)ⁿ .

3043241 Сумма двух или большего числа датированных сумм, погашаемых в различные даты:

1. Не имеет смысла;

2. Имеет смысл, если суммы выплачивают до одного года;

3. Имеет смысл, если суммы выплачивают до пяти лет;

4. Нет правильного ответа.

3052143. Датированные суммы одной и той же серии, определенные для различных дат, называются:

1. Погашаемыми;

2. Равновероятными;

3. Многомерными;

4. Эквивалентными.

3061324. При данной норме сложного процента две серии платежей являются эквивалентными, если:

1. Датированные суммы этих серий на любую общую дату используются на одну и ту же цель;

2. Датированные суммы этих серий на любую общую дату на заданную договорную величину;

3. Датированные суммы этих серий на любую общую дату являются равными;

4. Все ответы правильные.

307312. В качестве даты сравнения при составлении уравнения эквивалентности можно использовать:

1. Только настоящую дату;

2. Любую дату;

3. Только дату погашения;

4. Нет правильного ответа.

3082314. уравнения эквивалентности показывают, что они связывают величины трех типов: а) суммы погашения; б) даты погашения; в) нормы процентов; г) начальную сумму:

1. а); б); в);

2. а); б); г);

3. а); в); г);

4. б); в); г).

3091432. Когда серия обязательств заменяется единственным обязательством с суммой погашения, равной сумме сумм погашения всех обязательств серии, время выполнения этого обязательства при эквивалентной замене называется:

1. Датой обязательства;

2. Датой погашения;

3. Датой датирования;

4. Датой эквивалентности.

3102134. Процентные ставки разного вида, применение которых при одинаковых начальных условиях дают одинаковые финансовые результаты называют:

1. Эквивалентные средние суммы;

2. Датированные процентные ставки;

3. Эквивалентные процентные ставки;

4. Датированные суммы.

Глава 4 Аннуитеты

Аннуитет является последовательностью периодических платежей, обычно одинаковых, сделанных через одинаковые промежутки времени. Наиболее известными примерами аннуитетов являются платежи премий страхования жизни, платежи рассрочки, платежи ренты и т.д.

Период времени между двумя последовательными платежами называется интервалом платежаи может быть любой удобной продолжительности. Первоначально слово аннуитет относилось только к ежегодным платежам, но современное использование этого термина может предусматривать интервалы платежа любой продолжительности.

Сроком аннуитета является время от начала первого интервала платежа до окончания последнего интервала платежа. Когда срок аннуитета фиксирован, то есть когда срок начинается и заканчивается в определенные даты, аннуитет называется определенным (детерминированным) аннуитетом. Когда срок аннуитета зависит от некоторого неопределенного события, такого как смерть человека, аннуитет называется зависимым (случайным) аннуитетом.

Когда платежи производятся в моменты окончания интервалов платежа, аннуитет называется обыкновенным аннуитетом. Когда платежи производятся в начальные моменты интервалов платежа, аннуитет называется полагающимся аннуитетом. В дальнейшем слово аннуитет будет означать обыкновенный аннуитет, если не оговорено другое.

Предположим, что Иванов покупает автомобиль в рассрочку, выплачивая наличными 3 млн. руб. в день покупки и затем ежемесячно 1 млн. руб. в течение 24 месяцев, первый взнос по истечению 1 месяца после даты продажи. Ежемесячные взносы составляют обыкновенный аннуитет, срок которого начинается в день продажи и продолжается в течение двух лет. Интервал платежа равен 1 месяцу.

Все задачи об аннуитетах касаются полной стоимости серии платежей на некоторую заданную дату.