Серии датированных сумм

Сумма двух или большего числа датированных сумм, погашаемых в различные даты, практически не имеет смысла. Например, предположим, что 20000 руб. погашается через два года, а 30000 руб. погашается через пять лет. Сумма 20000 + 30000 = 50000 руб. не связана, с какой либо датой и поэтому мало о чем говорит. Однако если все рассматриваемые суммы преобразовать в эквивалентные датированные суммы с одной и той же датой погашения, то сумма таких эквивалентных сумм приобретает смысл и называется датированной суммой серии. Она будет изменяться в зависимости от даты, к которой преобразованы эквивалентные суммы. Для различных датированных сумм одной и той же серии справедливо следующее свойство 2: датированные суммы одной и той же серии, определенные для различных дат, являются эквивалентными.

Пусть А и В будут двумя датированными суммами, погашаемыми через а и b периодов начисления от настоящего времени. Пусть также U и V будут двумя датированными суммами этой серии, определенными для дат u и v (за единицу времени принимается период начисления). Представим эти данные на временной диаграмме:

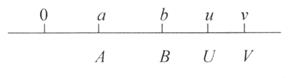
Преобразовывая значения А и В ко времени и согласно правилу эквивалентности и суммируя результаты, получим датированную сумму серии, погашаемую через u периодов:

U=A(1+i)^u-a+B(1+i)^u-b

Умножая обе части этого равенства на (1+i)^v-u и производя очевидные упрощения, получим другую датированную сумму серии, погашаемую уже через v периодов начисления,

U(1+i)^v-u=A(1+i)^v-a+B(1+i)^v-b.

Но правая часть этого равенства в точности равна V, так что , U(1+i)^v-u=V и условие эквивалентности U и V выполняется, что и доказывает справедливость свойства 2.

Как уже было выше отмечено, для сравнения двух итоговых сумм, погашаемых в различные даты, необходимо заменить их эквивалентными суммами, пересчитанными на одну и ту же дату. Величина разности полученных эквивалентных сумм будет различной в зависимости от использованной для сравнения даты. Также как и в случае сумм серий, разности, рассчитанные на различные даты, будут эквивалентными. Доказательство этого повторяет те же рассуждения, которые были использованы выше при анализе сумм серий на различные даты при рассмотрении свойства 2.