Финансовая эквивалентность в страховании
В преобладающем числе областей финансовой деятельности объектами приложения методов количественного анализа являются детерминированные процессы, описываемые верными рентами. Однако в страховании и при анализе некоторых инвестиционных проектов возникает необходимость в использовании условных рент, в которых важную роль играют вероятности наступления соответствующих событий (поступлений или выплат денег). Выплата ренты в страховании зависит от наступления страхового события. Такие ренты называются страховыми аннуитетами. Заранее число платежей в страховых аннуитетах, а часто и их срок, остаются неизвестными.
Согласно договору страхования страхователь уплачивает вперед страховщику некоторую сумму – премию. В свою очередь он (или иной выгодоприобретатель) имеет право получить страховую сумму S после наступления страхового события. Если вероятность наступления этого события g, то теоретически без учета прочих факторов (в том числе и факторов времени), премии P определяется как P=Sg
На практике премия, которая поступает страховой организации, обычно повышает величину нетто-премии, так как включает помимо нетто-премии и так называемую нагрузку, которая охватывает все расходы по ведению дела и некоторую прибыль страховой организации. Определение брутто-премии (нетто-премия плюс нагрузка) является чисто арифметической задачей, поэтому будем рассматривать только нетто-премии.
Пусть P – размер премии, gn – вероятность страхового события (например, смерть застрахованного через n лет после начала страхования). Если страховое событие произойдет на первом году страхования, то страховщик получит сумму P (пусть премия выплачивается в начале года), если же это событие наступит во втором году, то сумма премии равна 2P и так далее. Математическое ожидание такого ряда премии составит:
Pg1+2Pg2+…+nPgn.
Полученная величина хотя и обобщает все взносы застрахованного с учетом вероятностей их выплат, однако при суммировании соответствующих величин не принимается во внимание, что премии выплачиваются в разные моменты времени. С учетом этого фактора (с помощью дисконтирования сумм платежей) находим математическое ожидание современной стоимости (актуарная стоимость) взносов:
E(A)=P[g1+(1+v)g2+(1+v+v2)g3+…+(1+v+…+vn-1)gn],
где v – дисконтный множитель по ставке i.
Пусть страховая сумма выплачивается в конце года, в котором имел место страховой случай. Тогда математическое ожидание выплаты в первом году составит Sg1, во втором году Sg2 и так далее. Математическое ожидание с учетом фактора времени (аккуратная стоимость) выплат может быть определена как
E(S)=S(vg1+v2g2+…+vngn).
Исходя из принципа эквивалентности обязательств страховщика и страхователя, можно написать равенство
E(S)=E(A),
которое позволяет найти искомое значение нетто-премии P. Таков в общем виде теоретический подход к методу расчета нетто-премии, принятый в личном страховании.
Пусть теперь речь идет об имущественном страховании. Если можно полагать, что вероятность наступления страхового случая постоянны, то актуарная стоимость премии за n лет составит
E(A)=P[g+(1+v)g+…+(1+v+…+vn-1)g]=PgK,
Где K=n+ 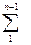 (n-t)vt.
(n-t)vt.
В свою очередь актуарная стоимость выплат страховых сумм находится как
E(S)=Sg 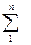 vt
vt
Из равенства актуарных стоимостей взносов и выплат находим искомый размер нетто-премии.
В практике страховых, или как часто называют, актуарных расчетов разработаны специальные приемы формирования упомянутых выше потоков платежей (страховых аннуитетов) и расчета их стоимости.
До обсуждения проблем формирования страховых аннуитетов, связанных с жизнью людей и их использования для расчетов премии и страховых резервов необходимо ознакомиться с методикой определения необходимых вероятностей и ряда вспомогательных величин, с помощью которых существенно упрощается решение соответствующих задач. Это таблицы смертности и коммутационные функции.
Дата добавления: 2019-10-16; просмотров: 639;
