ВЫВОД КИНЕТИЧЕСКОГО УРАВНЕНИЯ ПОСЛЕДОВАТЕЛЬНЫХ РЕАКЦИЙ. МЕТОД СТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ БОДЕНШТЕЙНА.

Этот метод основан на том, что концентрации промежуточных веществ в какой-то момент времени постоянны, т. е. скорость, рассчитываемая по этому веществу, приравнивается нулю. Таким образом, мы переводим дифференциальное уравнение в алгебраическое.

Существует алгоритм составления кинетического уравнения.

1.Расписываем механизм данной реакции по стадиям.

2. Выбираем промежуточное соединение (как правило, самое неустойчивое).

3. Записываем скорость по данному веществу, используя следующий прием: на стадиях, где это вещество образуется, кинетическое уравнение записываем со знаком «+», а там, где оно расходуется – со знаком «–».

4. Суммарную скорость приравниваем к нулю.

5. Составляем выражение для концентрации промежуточного вещества.

6. Это выражение подставляем в кинетическое уравнение скорость определяющей (лимитирующей) стадии.

Например: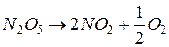

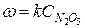экспериментально было получено, что реакция первого порядка

Предположим, что данная реакция протекает через следующие стадии, т. е. расписываем механизм:

1. 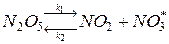( 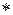– это обозначение неустойчивого вещества)

2.

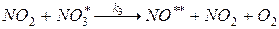
3.

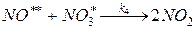
Выразим скорость реакции по веществу :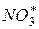

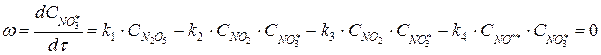
Из этого выражения найдем концентрацию :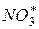

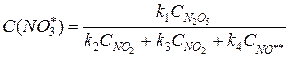
Теперь выразим концентрацию неустойчивого вещества :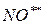

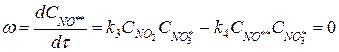
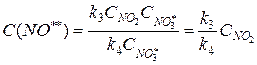
Подставим полученное выражение концентрации 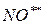в выражение концентрации :

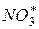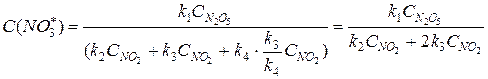
Подставляем полученное значение в кинетическое уравнение для последней лимитирующей стадии процесса:

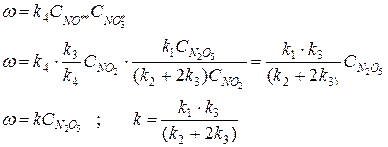
Таким образом, константа скорости этой реакции является совокупностью констант скоростей трех стадий, которые экспериментально определить нельзя. Экспериментально мы определяем константу скорости k, называемую эффективной константой скорости.