Методы проецирования
Правила построения изображений, излагаемые в курсе начертательной геометрии, основаны на методе проекций. Рассмотрение метода проекций начинают с построения проекции точки, на примере которого рассматривают все базовые понятия и правила проецирования.
Это не сужает круг решаемых задач в начертательной геометрии, т.к. все линии и поверхности можно представить как совокупность точек.
Центральное проецирование
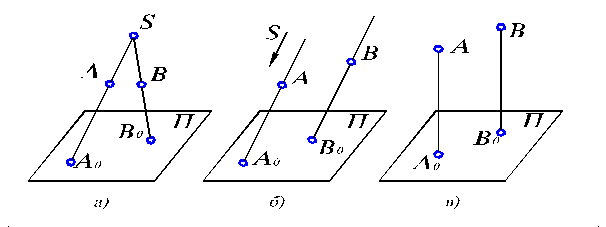
Наиболее общим методом проецирования является центральное проецирование (рис.1.1, а).
Рис. 1.1. Методы проецирования: а) центральное; б) параллельное; в) ортогональное.
Сущность центрального проецирования заключается в следующем: пусть даны плоскость П и точка S (SÏП). Возьмем произвольную точку А (АÏП, АÏS). Через заданную точку S и точку А проводим прямую SА и отмечаем точку А0, в которой эта прямая пересекает плоскость П. Плоскость П называют плоскостью проекций, точку S центром проецирования, полученную точку А0 – центральной проекцией точки А на плоскость П, прямую SА – проецирующей прямой. Аналогично можно получить проекцию любой другой точки, например точки В, на том же чертеже. Характерной особенностью получаемых проекций является то, что размеры геометрических объектов будут искаженными. Так, на указанном чертеже видно, что если соединить точки А и В прямой, то ее проекция А0В0 значительно больше в размерах, чем прямая АВ.
Наглядным примером центрального проецирования на практике может служить тень на некоторой поверхности (в частности, плоскости) какого-либо предмета, освещенного лампочкой (т.е. точечным источником света).
Параллельное проецирование
Частным случаем центрального проецирования является параллельное (рис. 1.1, б), когда центр проецирования находится в бесконечности. Тогда проецирующие лучи параллельны друг другу. Поскольку в природе трудно представить наглядно такой центр, то образным примером может служить тень, отбрасывыаемая каким-либо предметом, освещенным солнцем. В этом случае солнечные лучи можно считать параллельными друг другу.
Ортогональное проецирование
Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций (рис. 1.1, в), называется ортогональным проецированием.
В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение плоских изображений основано на этом методе.
Из принципов построения ортогональных проекций вытекают основные свойства ортогонального проецирования, которые здесь приведем без доказательства.
Свойства ортогонального проецирования:
v Проекция точки – точка.
v Проекция прямой – прямая.
v Проецирующий луч проецируется в точку.
v Точка принадлежит прямой линии, если одноименные проекции точки принадлежат одноименным проекциям прямой линии.
v Прямые в пространстве параллельны, если их одноименные проекции параллельны.
v Прямой угол проецируется в прямой, если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна к ней (Теорема о прямом угле).
v Прямая линия параллельна плоскости, если она параллельна любой прямой, принадлежащей заданной плоскости.
v Проекция плоской фигуры – плоская фигура.
v Решение задач начертательной геометрии и все дальнейшие построения основываются именно на этих свойствах.
Дата добавления: 2019-10-16; просмотров: 981;
