Графическое отображение прямой на комплексном чертеже
Следующим по сложности построения проекций после точки геометрическим объектом является прямая линия. Поскольку ее положение в пространстве однозначно определяется двумя точками, то и для определения положения проекций прямой также достаточно построить проекции двух точек. Поэтому для построения проекций прямой можно использовать все правила, касающиеся проецирования точки.
Прямые частного положения
Прямая называется прямой частного положения, если она занимает в пространстве частное положение, а именно либо параллельна, либо перпендикулярна одной из плоскостей проекций.
Прямые уровня
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.
а). Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.
б). Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.
в). Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.
Исходя из положения прямых уровня в пространстве — расположены на одинаковом расстоянии от какой-либо плоскости проекций, поэтому две проекции из трех параллельны соответствующим осям — их проекции выглядят, как показано на рис. 1.6.
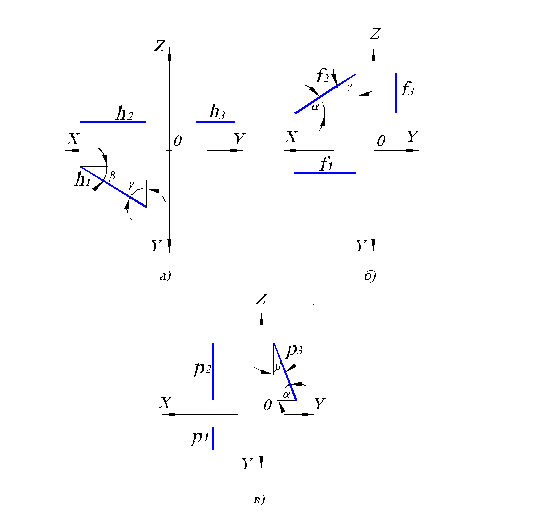
Рис. 1.6. Линии уровня на комплексном чертеже: а) горизонталь; б) фронталь; в) профильная линия уровня.
Горизонталь характеризуется тем, что ее фронтальная проекция параллельна оси ОХ. У фронтали горизонтальная проекция параллельна оси ОХ. При этом по правилу взаимосвязи проекций расстояние от f3 до оси OZ равно расстоянию от f1 до оси ОХ. У профильной линии уровня и фронтальная и горизонтальная проекции параллельны соответствующим осям, и следовательно, перпендикулярны оси ОХ.
Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.
Очевидно, что углы наклона проекций прямой к осям проекций характеризуют соответствующие углы наклона самой прямой к плоскостям проекций, а именно:
a — угол наклона прямой уровня к П1,
b — угол наклона прямой уровня к П2,
g — угол наклона прямой уровня к П3.
Проецирующие прямые
Проецирующей прямой называется прямая перпендикулярная одной из плоскостей проекций, а следовательно, параллельная двум другим плоскостям проекций.
а). Прямая, перпендикулярная горизонтальной плоскости проекций П1, называется горизонтально-проецирующей прямой и обозначается i.
б). Прямая, перпендикулярная фронтальной плоскости проекций П2, называется фронтально-проецирующей прямой и обозначается j.
в). Прямая, перпендикулярная профильной плоскости проекций П3, называется профильно-проецирующей прямой обозначается r.
Исходя из положения проецирующих прямых в пространстве, их проекции выглядят как показано на рис. 1.7.
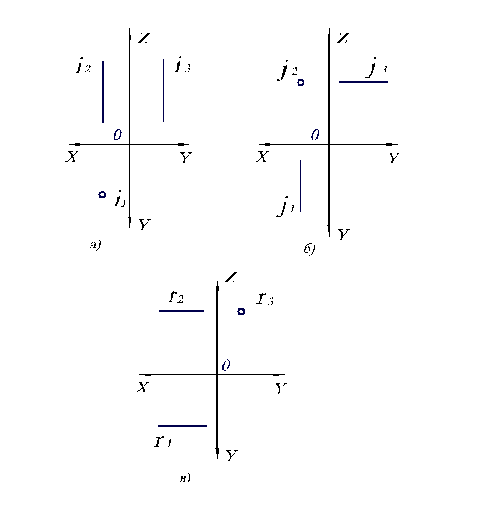
Рис. 1.7. Проецирующие прямые на комплексном чертеже: а) горизонтально-проецирующая прямая; б) фронтально-проецирующая прямая; в) профильно–проецирующая прямая.
Горизонтально-проецирующая прямая характерна тем, что ее горизонтальной проекцией является точка, а фронтальная и профильная проекции перпендикулярны соответственно осям ОХ, ОY. Фронтально-проецирующая прямая отличается тем, что ее фронтальной проекцией является точка, а горизонтальная и профильная проекции перпендикулярны соответствующим осям. У профильно-проецирующей прямой фронтальная и горизонтальная проекции параллельны оси ОХ, а профильная проекция — точка.
У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i2, i3, j1, j3, r1, r2 – это натуральные величины соответствующих прямых i, j, r.
Прямая общего положения
Прямой общего положения называется прямая, занимающая общее положение в пространстве, т.е. не параллельная ни к одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.
Естественно, что ни одна из проекций прямой общего положения не показывает ее натуральную величину, а также угол наклона к какой-либо из плоскостей проекций (рис. 1.8). Любая проекция такой прямой меньше самой прямой. Таким образом, для прямой общего положения верно утверждение, что ее натуральная величина больше любой проекции.
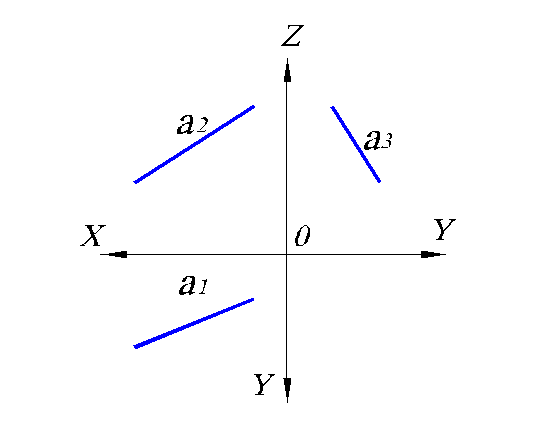

Деление отрезка прямой в заданном отношении
При делении отрезка прямой в заданном отношении используется теорема о подобии треугольников, известная из курса элементарной геометрии. Так, если необходимо отрезок АВ разделить в отношении 2:3, тогда и его проекции будут разделены в том же отношении. Для этого на одной из проекций (например, горизонтальной) из любой граничной точки (например, В) отрезка проведем прямую линию d в произвольном направлении (рис. 1.9). Затем отложим на ней 5 равных отрезков, после чего соединим полученную точку В* с точкой А1. Далее через вторую засечку на линии d проведем прямую, параллельную А1В*. На отрезке А1В1 получим точку С1, которая делит его в заданном отношении, т.е. В1С1 : А1С1=2 : 3.
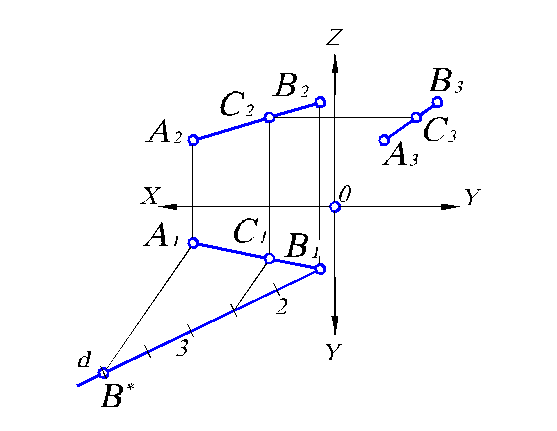

Проведя соответствующие линии проекционной связи, получим проекции точки деления на проекциях А2В2 и А3В3. Таким образом, разделив проекции отрезка в заданном отношении, мы тем самым решили задачу деления самого отрезка.
Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника
Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который можно сформулировать так: натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которого служит горизонтальная (фронтальная) проекция отрезка, другим – разность расстояний от граничных точек фронтальной (горизонтальной) проекции отрезка до оси ОХ. При этом углом наклона отрезка к горизонтальной (фронтальной) плоскости проекции является угол между гипотенузой прямоугольного треугольника и горизонтальной (фронтальной) проекцией отрезка.
Пусть задан отрезок СD. Из любой точки (например, D1) отрезка проведем перпендикуляр к нему (рис. 1.10.).
|
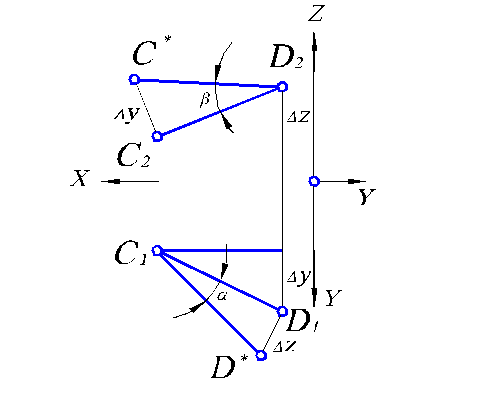
На нем, отложив отрезок длиной Dz, получим точку D*. После соединения точек D* и С1 получаем прямоугольный треугольник С1D1D*, в котором С1D* - натуральная величина отрезка СD, a - угол наклона отрезка СD к плоскости П1. Для определения угла наклона к плоскости П2 проведем аналогичные построения на фронтальной проекции. Здесь С*D2 – натуральная величина СD , b - угол наклона СD к плоскости П2.
Безосные чертежи
Построение недостающих проекций геометрического объекта возможно и в том случае, когда оси проекций на чертеже отсутствуют.
Если указаны горизонтальная и профильная проекции некоторой точки А, то ее фронтальная проекция А2 находится на пересечении линий связи: горизонтальной, выходящей из точки А3, и вертикальной, выходящей из точки А1 (рис. 1.11).
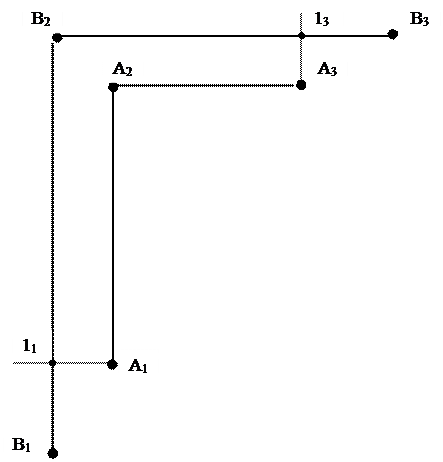 |
Рис. 1.11. построение точек на безосном чертеже.
Если на безосном чертеже показаны фронтальная и какая-либо из двух других проекций заданной точки, то невозможно построить недостающую третью проекцию, используя проекции только этой точки. Необходимо воспользоваться изображенными на чертеже проекциями какой-либо другой точки.
Пусть на том же самом чертеже, где заданы все три проекции точки А, показаны горизонтальная В1 и фронтальная В2 проекции точки В (см. рис. 1.11). Учитывая правило взаимосвязи проекций, можно утверждать, что точка В3 дальше от воображаемой оси ОZ, чем точка А3, настолько же, насколько точка В1 дальше от воображаемой оси ОХ, чем точка А1. Остается воспроизвести на чертеже указанное правило. Для этого из точки А1 проводим горизонтальную прямую до пересечения с линией связи В1В2. Получаем точку 11. Затем из точки В2 проводим горизонтальную линию связи (или перпендикуляр к В1В2). Из точки А3 проводим вертикальную прямую до пересечения с горизонтальной линией связи, где получаем точку 13. Наконец на продолжении горизонтальной линии связи откладываем расстояние, равное В111, и находим положение точки В3.
Действительно, точка В1 дальше от оси ОХ, чем А1, на расстояние В111; точка В3 дальше от оси ОZ, чем А3, на расстояние В313; из построений следует, что В111=В313. Это и подтверждает правильность построений.
Для самопроверки можно провести ось ОХ через точку А1. Тогда ось ОZ пройдет через точку А3. После этого построение проекции В3 по заданным В1 и В2 выглядит очевидным.
Аналогично можно построить недостающую горизонтальную проекцию В1 по заданным В2 и В3. В этом случае построения выполняются в обратном порядке.
Разумеется, следует иметь в виду, что если горизонтальная проекция точки ближе к оси ОХ, т.е. лежит выше, то и ее профильная проекция ближе к оси ОZ, т.е. лежит левее на чертеже.
Дата добавления: 2019-10-16; просмотров: 840;
