Переместительное свойство сходящихся рядов

Фразу «от перемены мест слагаемых сумма не меняется» в школе так вбивают в голову, что она кажется аксиомой. Она действительно верна, если слагаемых конечноечисло. Но будет ли она верна, если слагаемых бесконечно много? Ответу на этот вопрос и посвящены две следующие теоремы.

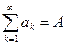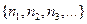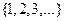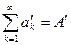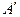Пусть дан сходящийся ряд (ряд А). Пусть есть некоторая перестановка чисел , причем чисел переставлено бесконечно много. Рассмотрим ряд (ряд ), где 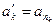. Будет ли выполняться равенство ?

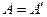Теорема. Если ряд А сходится абсолютно, то ряд А’ тоже абсолютно сходится и имеет ту же сумму.

Доказательство.

1. Пусть 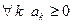и 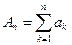есть частная сумма рада А. Так как все слагаемые неотрицательны, то, очевидно, все частные суммы меньше суммы ряда А.

Рассмотрим теперь частные суммы ряда :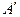

.

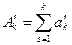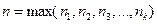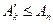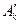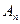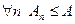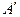Возьмем . Тогда очевидно, что , так как в сумме не большеслагаемых, чем в сумме . Но , и поэтому и ряд сходится. При этом верно соотношение .

Но ряд А также получается из ряда 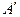перестановкой слагаемых. Поэтому должно одновременно выполняться и неравенство 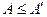. Отсюда и следует, что .

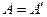2. Пусть теперь слагаемые ряда А могут иметь произвольный знак, но ряд, составленный из их модулей, сходится: .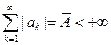

Основная идея дальнейшего состоит в том, чтобы разбить ряд А на два ряда, в одном их которых будут собраны все положительные слагаемые, а в другом - все отрицательные. Представим себе, что мы просматриваем все слагаемые ряда А по порядку номеров. Если окажется, что 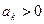, то обозначим его через 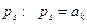(величины 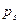нумеруются в порядке их появления). Если окажется, что 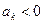, то введем величину 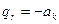(величины 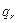также нумеруются в порядке их появления. Таким образом, вместо одного ряда А появятся два ряда 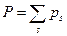и .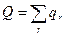

Так как частные суммы этих рядов удовлетворяют неравенствам 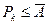, , 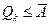то оба этих ряда сходятся. Далее очевидно, что 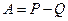и .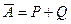

Но перестановка слагаемых в ряде А приведет лишь к перестановке слагаемых в рядах P и Q. Все слагаемые этих рядов положительные, следовательно, согласно п.1, от такой перестановки их суммы не изменятся, а поэтому не изменится сумма ряда А. <

Итак, в абсолютно сходящихся рядах от перестановки слагаемых из сумма не меняется. А как насчет неабсолютно сходящихся рядов?

Теорема Римана. Если ряд 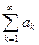сходится неабсолютно, то, какое бы ни взять число В (конечное, или равное ± ¥), можно так переставить слагаемые в ряде, что его сумма станет равной В.

Так что от перестановки местами слагаемых сумма все-таки может меняться!

Доказательство.

1. Проделаем с нашим рядом ту же процедуру, что и в предыдущей теореме, и построим ряды P и Q. Но теперь ситуация меняется кардинально: есть конечное число, а 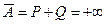. Это может быть лишь в том случае, когда 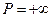и , то есть ряды P и Q расходящиеся.

2. Возьмем конечное число В. Пусть, для определенности, 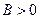. Начнем строить новый ряд 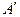следующим образом.

Начнем сначала складывать положительные слагаемые из ряда Р. Так как этот ряд расходящийся, то есть его сумма равна + ¥, то на каком-то шаге накопленная сумма превзойдет число В. Мы остановимся, как только это произойдет в первый раз, то есть будет выполнено следующее

.

А теперь начнем прибавлять отрицательные слагаемые ряда А, то есть вычитать слагаемые ряда Q. Сумма этого ряда также равна + ¥, и поэтому на каком-то шаге накопленная сумма обязательно станет меньше В. Мы снова остановимся, как только это произойдет в первый раз, то есть будет выполнено следующее

,

.

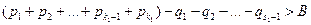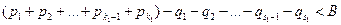Снова начнем прибавлять положительные слагаемые, пока накопленная сумма не превзойдет В, затем снова отрицательные, пока накопленная сумма не станет меньше В, и т.д. и т.д.

Эту процедуру можно проиллюстрировать следующим рисунком:

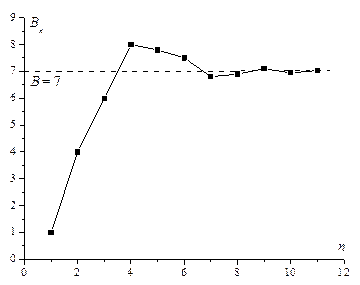
Каждый раз членов рядов P и Q берется не больше, чем необходимо для первого осуществления требуемого неравенства. Тогда отклонения накопленных сумм от В по модулю не превысят последнего написанного члена. В силу сходимости ряда А его общий член стремится к нулю. Следовательно, накопленные суммы стремятся к числу В, так что построенный ряд сходится и его сумма равна именно В.

3. Пусть .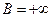

Возьмем последовательность чисел 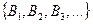, такую, что

, .

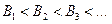Трудность заключается в том, что нам надо разместить не только положительные, но и отрицательные члены ряда. Поэтому поступаем следующим образом:

Сначала складываем положительные слагаемые до тех пор, пока их сумма в первый разне превысит число В₁:

.

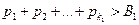Затем добавляем одноотрицательное слагаемое и снова добавляем положительные, пока их сумма в первый разне превысит число В₂:

.

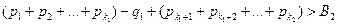Снова добавляем одно отрицательное слагаемое и снова добавляем положительные, пока их сумма в первый разне превысит число В₃ и т.д. Так как чисел 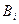счетное множество, то разместятся не только все положительные, но и все отрицательные слагаемые.

Очевидно, что сумма построенного таким образом ряда равна + ¥. <

Пример.

Рассмотрим ряд

,

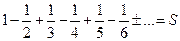который сходится по признаку Лейбница. Переставим его слагаемые по следующему правилу: после положительного слагаемого идут два отрицательных:

.

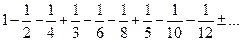Из экономии, мы не будем доказывать, что этот ряд сходится - попробуйте сделать это сами.

Каждая тройка слагаемых имеет следующую структуру

,

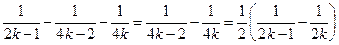Тогда построенный ряд принимает вид

,

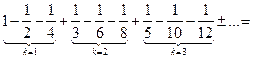
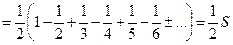так что сумма построенного ряда уменьшилась в два раза.

Таким образом, в неабсолютно сходящемся ряде можно переставлять местами только конечноечисло слагаемых, а вот переставлять местами бесконечноечисло слагаемых нельзя - можно получить все, что угодно.

Перемножение рядов

Пусть даны два ряда

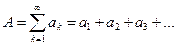(ряд А) и

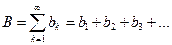(ряд В).

Как определить произведение этих рядов?

Рассмотрим бесконечную матрицу

,

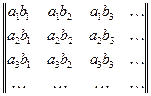составленную из всевозможных произведений вида 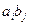. Нам надо сложить все элементы этой матрицы. Как это сделать? Моно, например, по диагоналям складывать

, (*)

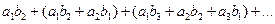а можно и так

,

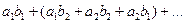можно еще тысячами разных способов. Но где гарантия, что все эти ряды имеют одну и ту же сумму?

Теорема Коши. Если ряды (А) и (В) сходятся абсолютно, то их произведение, составленное из слагаемых вида 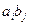, взятых в любом порядке, также сходится и имеет своей суммой .

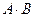Доказательство.

Рассмотрим ряд вида

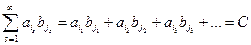
в которое входят все комбинации типа 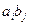, и рассмотрим его частную сумму

.

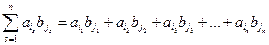Пусть 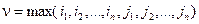. Тогда

,

где 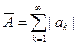, 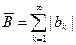. Следовательно, ряд 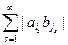сходится. В силу этого ряд 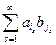сходится абсолютно и поэтому его слагаемые можно располагать в любом порядке. Беря частные суммы ряда С в виде

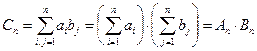
и поэтому . <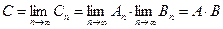

на практике чаще всего суммируют по диагоналям бесконечной матрицы, как в (*).

Двойные ряды

Обобщением рассмотренной выше ситуации является следующая. Дана бесконечная матрица

.

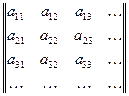Рассмотрим суммы 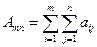. Рассмотрим двойной предел, когда m и n одновременно независимо друг от друга стремятся в + ¥ (более строгое определение понятия двойного предела смотрите в следующей главе):

,

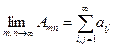который называется двойным рядом, и обозначается символом .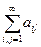

Кроме этого можно рассмотреть и так называемые повторные пределы, когда в + ¥ уходит сначала n, а потом т

,

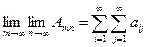или, наоборот, сначала т, а потом п

.

Они называются повторными рядами.