Признаки сходимости
Теорема 1. для того, чтобы бесконечное произведение сходилось необходимо и достаточно, чтобы сходился ряд 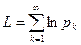 .
.
Доказательство.
Имеем
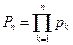 ;
; 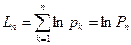 ;
; 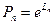 .
.
Используя непрерывность логарифмической и показательной функций, получаем:
А) 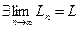 Þ
Þ 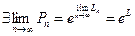 .
.
Б) 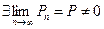 Þ
Þ 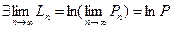 . <
. <
Так как 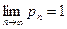 , то представим
, то представим 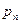 в виде
в виде 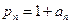 . Тогда
. Тогда 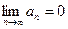 .
.
Теорема 2. Пусть, начиная с некоторого N, все 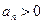 . Тогда, для сходимости бесконечного произведения необходимо и достаточно, чтобы сходился ряд
. Тогда, для сходимости бесконечного произведения необходимо и достаточно, чтобы сходился ряд 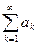 .
.
Доказательство.
Так как 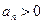 ,то
,то 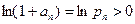 . Далее, так как
. Далее, так как 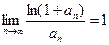 , то ряды
, то ряды 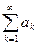 и
и 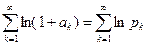 сходятся или расходятся одновременно. <
сходятся или расходятся одновременно. <
Теорема 3. Из сходимости рядов 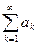 и
и 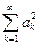 следует сходимость бесконечного произведения.
следует сходимость бесконечного произведения.
Доказательство.
Примем без доказательства неравенство 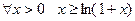 . Можете попытаться доказать его сами.
. Можете попытаться доказать его сами.
Далее, применяя правило Лопиталя, легко получить, что
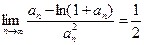 .
.
Далее идет следующая цепочка следований:
Ряд 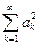 сходится Þ ряд
сходится Þ ряд 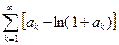 также сходится. Но так как сходится ряд
также сходится. Но так как сходится ряд 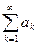 , то сходится и ряд
, то сходится и ряд 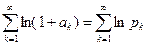 Þ бесконечное произведение сходится. <
Þ бесконечное произведение сходится. <
Еще кое-что
Бесконечное произведение 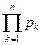 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 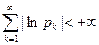 . Если ряд
. Если ряд 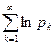 сходится, но
сходится, но 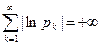 , то бесконечное произведение
, то бесконечное произведение 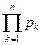 называется неабсолютно сходящимся
называется неабсолютно сходящимся
В абсолютно сходящемся произведении можно как угодно переставлять сомножители - от этого оно не изменится. В неабсолютно сходящемся произведении перестановка сомножителей может изменить значение бесконечного произведения.
Дата добавления: 2019-07-26; просмотров: 437;
