Сочетательное свойство сходящихся рядов

Рассмотрим два ряда

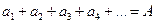
который будем называть рядом (А), и ряд

,

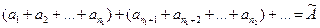который будем называть рядом ( ).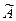

Теорема. Если ряд (А) сходится, то ряд ( 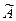) тоже сходится и имеет ту же сумму.

Доказательство.

Пусть 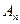есть частная сумма ряда (А), то есть 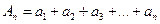. Рассмотрим теперь частные суммы ряда ( 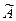). Имеем

; ; ; … .

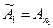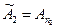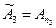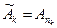Но тогда, если 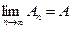, то и 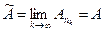, потому, что последовательность 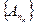есть подпоследовательность последовательности . <

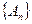Замечания.

1. Это свойство нельзя применять наоборот, то есть из сходимости ряда ( 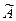) не следует сходимость ряда (А). Другими словами, в сходящемся ряду собирать слагаемые в группы и заключать эти группы в скобки можно,а вот раскрывать скобки, вообще говоря, нельзя, точнее, надо делать это очень осторожно. Это можно делать лишь тогда, когда ряд, получающийся после раскрытия скобок, является сходящимся рядом, а это надо доказывать.

Пример. Ряд

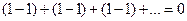
сходится и сумма его равна нулю, а вот ряд, полученный после раскрытия скобок,

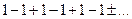
расходится, так как его общий член не стремится к нулю.

2. Это свойство невернодля расходящихся рядов, то есть в расходящемся ряду собирать слагаемые в группы и заключать эти группы в скобки нельзя.

Пример. Ряд

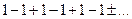
расходится, но ряды

,

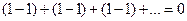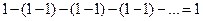
сходятся, и имеют разные суммы.