Выравнивание статистических рядов
Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем, что число наблюдений ограничено. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает присущую ему закономерность. На практике при обработке статистических данных часто приходится решать вопрос о том, как подобрать для полученного статистического ряда теоретическую кривую распределения, выражающую существенные черты статистического материала. Такая задача называется задачей выравнивания (сглаживания) статистических рядов. Задача выравнивания заключается в том, чтобы подобрать теоретическую кривую, наилучшим образом описывающую данное статистическое распределение.
Как правило, принципиальный вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи, а в некоторых случаях просто с внешним видом статистического распределения.
Следует иметь в виду, что любая аналитическая функция f(t), с помощью которой выравнивается статистическое распределение, должна обладать основными свойствами плотности распределения:
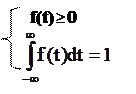 |
Предположим, что выбрана функция f(t), удовлетворяющая необходимым условиям, с помощью которой мы хотим выровнять данное статистическое распределение. В выражение этой функции входит несколько параметров а,в,с,... . Требуется подобрать эти параметры так, чтобы функция f(t) наилучшим образом описывала данный статистический материал. Один из методов, применяемых для решения этой задачи - это метод моментов.
Согласно методу моментов, параметры а,в,с... выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характеристикам. Например, если теоретическая кривая f(t) зависит только от двух параметров а и в, эти параметры выбираются так, чтобы математическое ожидание (mt) и дисперсия (Dt) теоретического распределения совпадали с соответствующими статистическими характеристиками.
Допустим, требуется выровнять статистическое распределение с помощью нормального закона:
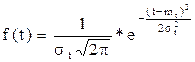 (3)
(3)
Для этого вычислим статистическое среднее:
m 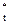 =t
=t 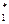 P
P 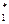 +t
+t  P
P  +…+t
+…+t 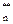 P
P 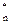 =
= 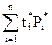 ,
,
где t 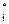 - середина интервала
- середина интервала 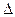 t.
t.
Статистическая дисперсия находится из выражения
 ,
,
где 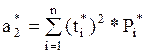 - второй начальный момент.
- второй начальный момент.
Напишем выражение для нормального закона:
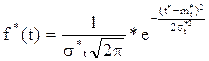 .
.
Вычисляем значение f*(t) на середине интервалов t  . На основе полученных значений построим на одном графике гистограмму и выравнивающую ее кривую.
. На основе полученных значений построим на одном графике гистограмму и выравнивающую ее кривую.
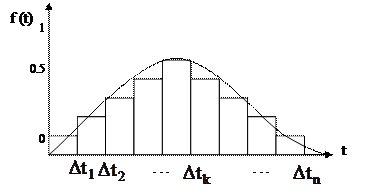 |
Рисунок 3.5.
На рисунке 3.5 показан пример сглаживающей кривой для распределения случайной величины по нормальному закону.
Дата добавления: 2017-10-09; просмотров: 1380;
