Понятие изоквант и изоклиналей мультипликативной функции

Изокванта, иначе, линия уровня на плоскости KL, — это множество тех точек плоскости, для которых F (К, L) = Х₀ = const.

Для МПФ изокванта имеет вид:

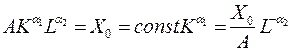, т.е. изо кванта – гипербола, асимптоты у которой оси координат. Для разных К, L, лежащих на одной конкретной изокванте, выпуск равен одному и тому же значению X₀, а это эквивалентно взаимозаменяемости ресурсов.

Поскольку на изокванте F (К, L) = Х₀ = const, то

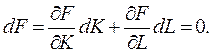
Т.к. 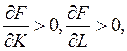то dK и dL имеют разные знаки. Если dL < 0, что означает сокращение объема труда, то dK > 0, т.е. выбывший в объеме 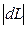труд замещается фондами в объеме dK.

Изоклинали - это линии наибольшего роста ПФ. Они ортогональны линиям нулевого роста, т.е. изоквантам. Т.к. направления наибольшего роста в каждой

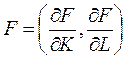точке (К, L) задается градиентом , то уравнение изоклинали имеет вид:

.

Для мультипликативной ПФ:

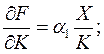
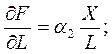
а изоклиналь имеет вид:

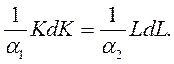
Решение этого уравнения:

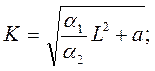
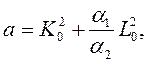
где 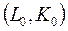– координаты точки, через которую проходит изоклиналь.

Самая простая изоклиналь проходит через начало координат при 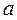= 0 и имеет вид прямой:

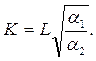
Модель Леонтьева

Модель Леонтьева - это статическая модель межотраслевой экономики.

Допущения, принятые при моделировании:

• в экономической системе все операции производятся с п продуктами;

• каждая отрасль производит только один продукт;

• совместное производство различных продуктов исключено;

• каждая отрасль производит свой продукт.

Под производственным процессом в каждой отрасли понимают преобразование некоторых (иногда всех) типов продуктов в определенный продукт.

При этом соотношение затраченного продукта и выпускаемого постоянно, т.е. для производства единицы j-го продукта затрачивают a_ij единиц i-го продукта.

x_i - валовой выпуск j-го продукта за год, он состоит из производственного потребления во всех отраслях и конечного (непроизводственного) потребления.

Чистый выпуск i-го продукта равен:

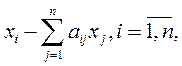
где a_ij - производственное потребление i-го продукта всеми отраслями.

у_i - конечный спрос на i-й продукт равен:

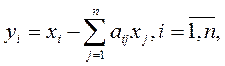(1)

В матричном виде формула (1) запишется так:

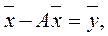
где

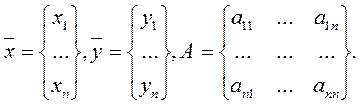
Это и есть статическая модель Леонтьева.

Считая спрос у_i — заданным, определяют n отраслевых выпусков х_i, зная расходный коэффициенты а_ij,. Это прямая задача.

Обратная задача: по заданным валовым выпускам определяют объем ко­нечного спроса у_i на каждый вид продукта n.

Это задача линейного программирования.

Коэффициент прямых затрат a_ij, объемы конечного спроса у_i и валовые выпуски х_i, - положительные.

Система работоспособна, если разрешима в положительных х_i

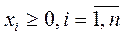
Двойственная задача: система линейных уравнений для цен продуктов P_j:

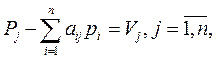
где 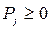— чистый доход от единицы выпуска j-ой отрасли;

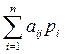— сумма издержек на единицу выпуска;

- добавленная стоимость на единицу выпуска j-ой отрасли.

Величины x_i, y_j могут измеряться как в натуральных, так и в стоимостных единицах выражения. Соответственно межотраслевой баланс может быть натуральный или стоимостной.