Описание поведения производственных фирм на функциональном уровне.

2. Определение максимального выпуска однопродуктовой фирмы, заданной производственной функцией Кобба-Дугласа:

Пусть производственная фирма выпускает один вид продукции или много видов, но в постоянной структуре, тогда обозначим X - годовой выпуск фирмы в натурально-вещественной форме (т.е. число единиц продукции одного вида или число многономенклатурных агрегатов).

Для производства продукции используется труд L - среднее число занятых в год, либо отработанные за год человеко-часы, и прошлый труд К в виде средств труда (основные производственные фонды) и предметы труда М (затраченные за год топливо, энергия, сырье, комплектующие и т.д.).

Каждый из этих трех агрегированных видов ресурсов (труд, фонды и материалы) имеет определенное число разновидностей (труд разной квалификации, оборудование различного вида и т.п.).

Обозначим вектор-столбец возможных объемов затрат различных видов ресурсов через х = (х₁,...,х_n). Тогда технология фирмы определяется ее производственной функцией, отражающей связь между затратами и выпуском:

X=F(x).

Функция F(x) непрерывная, дважды дифференцируемая и неоклассическая, т.е. гладкая и удовлетворяющая условиям:

1. F (0, L) = F (К, 0) = 0 - при отсутствии одного из ресурсов производство невозможно;

2. 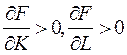– с ростом ресурсов выпуск растет;

3. 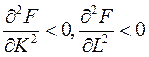– с увеличением ресурсов скорость роста выпуска замедляется.

Кроме того, матрица вторых производных функции F(x) определена.

Если цена единицы продукции - Р, а цена единицы ресурса j-го вида -W_j, 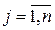, то каждому вектору затрат х отвечает прибыль:

П(x) = pF(x) – Wx (1)

Цены ресурсов имеют естественный смысл:

¾ если х_j - среднегодовое число занятых определенной профессии, то W_j - годовая зарплата одного работника данной профессии;

¾ если х_j - покупные материалы (топливо, энергия и т.д.), то W_j – покупная цена единицы данного материала;

¾ если х_j - производственные фонды определенного вида, то W_j - годовая арендная плата за единицу фондов или стоимость поддержания единицы фондов в исправности, если фирма владеет этими средствами.

В выражении (1) 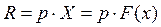- стоимость годового выпуска фирмы (или ее годовой доход); 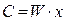- издержки производства или стоимость затрат фирмы за год.

Если нет других ограничений на размеры ресурсов, кроме их неотрицательности, то задача на максимизацию прибыли имеет вид:

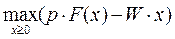(2)

Это задача нелинейного программирования с п условиями неотрицательности 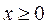. Необходимое условие ее решения является выполнение условий Куна-Таккера:

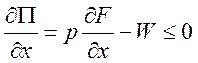
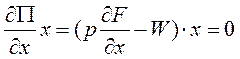(3)

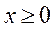
в точке х^* – оптимум

Если в оптимальном решении использованы все виды ресурсов, а х^* > 0, то условие (3) имеет вид:

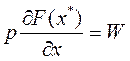, или (4)

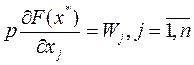
т.е. в предельной

Такое же по форме решение имеет задача на максимум выпуска при заданном объеме издержек:

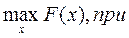
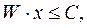(4a)

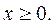
Это задача нелинейного программирования с одним линейным ограничением и условием неотрицательности переменных.

Для решения такой задачи строится функция Лагранжа, или вспомогательный функционал:

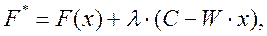
затем ищут его максимум при условии неотрицательности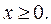

Для этого необходимо выполнение условий теоремы Куна-Таккера:

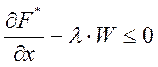
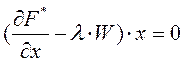(5)

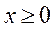
Эти условия совпадают с условиями (3), если где 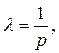где р - цена единицы продукции.

Пример.

Определить максимальный выпуск однопродуктовой фирмы, заданной производственной функцией Кобба-Дугласа:

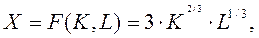(5a)

если на аренду фондов и оплату труда выделено 150 ден. ед.,

стоимость аренды единицы фондов W_K = 5 ден. ед./ед. фондов,

ставка заработной платы WL = 10 ден.ед./чел.

Какова предельная норма замены одного занятого фондами в оптимальной точке?

Решение.

Т.к. F (0, L) = F (К, 0) = 0, то в оптимальной точке 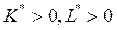. Условия (5) имеют вид:

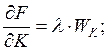
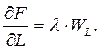(6)

Для производственной функции (5а):

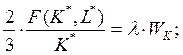
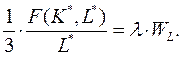
Разделив первое уравнение на второе, получим:

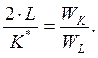
Подставив это соотношение в уравнение ограничения 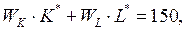найдем:

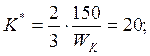
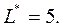
Графически решение имеет вид:

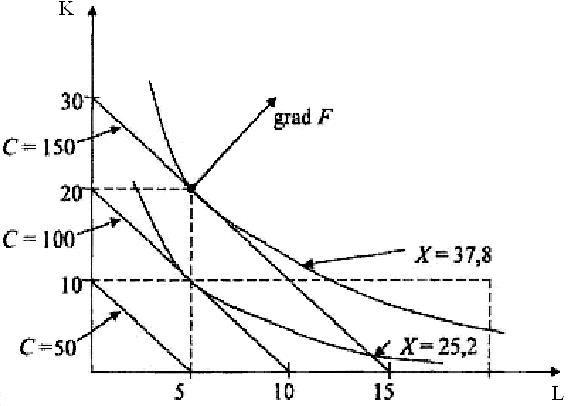
а) линии постоянных издержек С- изокосты;

б) линии постоянных выпусков для Х= 25,2; Х= 37,8 - изокванты.

Изокосты описываются уравнением:

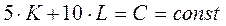
Изокванты описываются уравнением:

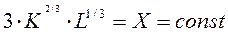
В оптимальной точке 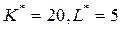изокванта X = 37,8 и изокоста С = 150, проходящие через эту точку, касаются, т.к. по (6) нормали к этим кривым, заданные градиентами 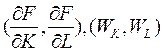коллинеарны.

Норма замены труда фондами в оптимальной точке:

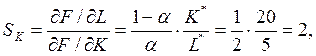
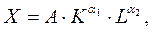
где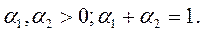

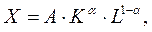
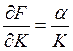– предельный продукт фондов;

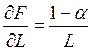– предельный продукт труда (производительность труда).

Решая задачу фирмы (2):

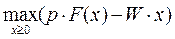
находим оптимальный набор ресурсов X* > 0; этому набору отвечает одинаковое значение издержек .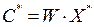

Решим теперь задачу на максимум прибыли при заданных издержках (4а).

Если F(x) - неоклассическая функция, то в оптимальном решении 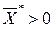, причем это решение единственно. Таким образом, с одной стороны:

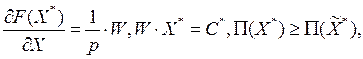
с другой:

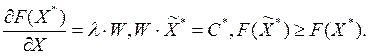
Поскольку:

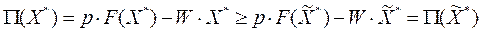
и 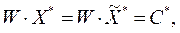то

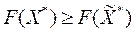, но 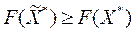поэтому

.

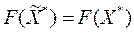Т.к. решение задачи (2) единственно, то .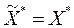

Таким образом, если задача на максимум прибыли имеет единственное ре­шение X* > 0, то ей отвечает задача на

причем последняя имеет такое же решение как и

Геометрическое место точек касания изокост и изоквант при разных значениях издержек С определяет долгосрочный путь развития фирм Х(С), т.е. показывает, как будет увеличиваться (уменьшаться) выпуск, если издержки возрастут (или уменьшатся).