Основная формула теории регулирования

Методы регулирования основаны на использовании обратной связи. Рассмотрим простую систему регулирования, имеющую один вход X и выход Y(рис.3.4).

Имеется некоторая регулируемая система S, которая подвергается определенным воздействиям X, дающим в итоге требуемый результат Y.

Результат воздействует на регулятор R, который, в свою очередь, воздей­ствует на регулируемую систему. Комплекс регулируемой системы и регу­лятора составляет систему регулирования. Преобразование состояния входа X в состояние выхода Y формально можно отобразить как: Y = SX. Этот способ отображения соответствует разомкнутому контуру управле­ния. Как показано на рис. 3.4, состояние выхода регулируемой системы S передается на вход регулятора R, выходом которого является величина АХ. Это состояние прибавляется к состоянию входа системы S: X + ΔХ.

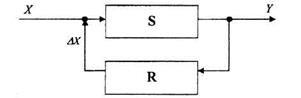
Рисунок 3.4 Система регулирования

Предположим, что регулируемая система работает как пропорцио­нальный преобразователь: Y=SX.

При S > 1 пропорциональное преобразование называется усилением, а при S < 1 - ослаблением.

Показатель S= 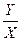называется пропускной способностью регулируемой системы.

Предположим также, что регулятор тоже осуществляет пропорцио­нальное преобразование, а его пропускная способность равна R. Тогда ΔХ = RY. С учетом воздействия регулятора состояние выхода регулируемой системы определится как:

Y = S(X + ΔХ) = S(X + RY) = SX + SRY.

Отсюда

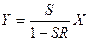. (3.15)

Выражение (3.15) является основной формулой теории регулирова­ния. Приведенная формула дает возможность рассчитать необходимое зна­чение входной величины, чтобы при заданных параметрах системы S и R получить на выходе искомый результат У. Принимая во внимание то, что 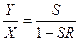, выражение 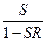называется пропускной способностью системы регулирования. Из основной формулы теории регулирования вытекает специфическая роль регулятора. При R = 0 пропускная способ­ность регулируемой системы была бы равна S: Y = SX. Наличие регулятора требует введения множителя 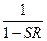, который характеризует его действие. Сомножитель 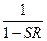выражает действие обратной связи в системе регулирования, и его называют оператором или мультипликатором обрат­ной связи.

Регулирование как функция управления получила широкое примене­ние в исследовании экономических систем управления.

Основные свойства и характеристики регулируемых систем изуча­ются технической кибернетикой в разделе теории автоматического управ­ления.