Многокритериальная система управления

Для многих сложных систем получить критерий эффективности в виде скалярной функции не представляется возможным. В этом случае ис­пользуется векторный критерий, составляющими которого являются само­стоятельные, независимые критерии. Такие системы называются многокритериальными.

Паллиативным решением является искусственное введение коэф­фициентов, позволяющих получить линейную комбинацию составляю­щих векторного критерия, приводя его таким образом к скалярному ви­ду. Однако, принимая во внимание независимость составляющих крите­риев, процедура определения предпочтений на множестве критериев и введение обобщенного критерия представляют зачастую большую слож­ность. Достаточно эффективным способом, используемым в случае век­торного критерия, является выбор управлений, оптимальных по Парето. Множество оптимальных по Парето решенийсоставляют такие, ни одно из которых не доминируется в определенном смысле никаким дру­гим решением из этого множества. Таким образом, каждое из множества оптимальных по Парето управлений лучше любого другого по одному из независимых критериев.

Иерархические системы управления

Важный класс систем управления образуют системы произвольной природы (технические, экономические, биологические, социальные) и на­значения, имеющие многоуровневую структуру в функциональном, орга­низационном или каком-либо ином плане. Характерными признаками ие­рархических систем управления (ИСУ) являются: вертикальная деком­позиция системы на подсистемы, приоритет подсистем верхнего уровня по отношению к нижележащим, наличие обратных связей между уровнями. Широкое использование и универсальность ИСУ обусловлены рядом пре­имуществ по сравнению с системами радиального (централизованного) управления:

• свобода локальных действий в рамках наложенных ограничений;

• возможности целесообразного сочетания локальных критериев функционирования отдельных подсистем и глобального критерия оптимальности системы в целом;

• возможности сжатого, агрегированного представления актуальной информации о результатах управления, поступающей по каналам обратной связи;

• повышенная надежность системы управления, наличие свойств управляемости, адаптивности, организованности и ряда других свойств, специфичных для конкретных систем;

• универсальность концепции управления и подходов к решению задач управления в ИСУ;

• экономическая целесообразность по сравнению с системами управления иной структуры. Последнее качество требует обоснования в каждом конкретном случае.

Теория управления ИСУ включает следующие основные разделы:

• структурный анализ и синтез ИСУ;

• проблема координации в ИСУ;

• оптимизация функционирования ИСУ.

Задачи, решаемые в названных разделах, будут рассмотрены в соот­ветствующих главах настоящего учебника.

Принцип иерархичности управления является выражением целост­ности систем; он, предопределяя организованность, позволяет найти спо­собы управления сложными системами. Если организованность системы отсутствует, невозможно определить задачи управления даже для про­стых объектов.

Этот принцип предусматривает способ расчленения системы на эле­менты и взаимодействующие подсистемы и многоступенчатого построе­ния управляющих систем, в которых функции управления распределяются между соподчиненными частями. В расчлененной системе одна часть ока­зывается «вложенной» в другую и является ее структурной составляющей. В такой системе существует взаимосвязь подсистем по одним отношениям и их свойствам и независимость по другим.

Определение 3.4 (общая задача оптимизаиии):пусть Q: M→Q -некоторая функция, отображающая множество М в множество Q, которое упорядочено отношением «≤«. Тогда задача оптимизации может быть сформулирована следующим образом: для данного подмножества 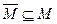найти такое 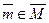, что для всех 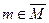выполняется условие:

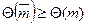(3.13)

Множество М является множеством решений задачи управления, множество 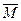- множеством допустимых решений, функция Q - целевой функцией, a Q — множеством оценок. Элемент 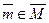, удовлетворяющий условию (3.13) при всех 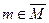, называется решением задачи оптимизации,задаваемой парой (Q, ).

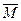Зачастую функцию Q определяют с помощью функций:

P:M→Y, Q:MxY→Q,

Q(m)=Q(m, P(m)). (3.14)

В этом случае функцию Р называют выходной функцией, а функцию Q - функцией качества или оценочной функцией. Задача оптимизации то­гда определяется тройкой (P, Q, 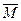) или парой P(P, Q), если 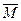= М.

Определение 3.5: система 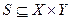называется системой принятия решений, если существует такое семейство задач принятия решений Dx, х 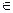X, решения которых принадлежит множеству M, и такое отображение Р: М →У, что для любого х 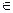Х и y 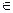Y пара (х, у) принадлежит системе S тогда и только тогда, когда найдется такое 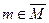, что m является решени­ем задачи Dx, а Р(m) = у,

Следствие: любую систему управления S можно представить как систему принятия решений и наоборот, просто опираясь на предположение о целесообразности ее поведения.

Принятие решений в системе управления производится на основе от­бора и преобразования информации. Цитируя У. Р. Эшби, можно отметить, что «любая система, выполняющая подходящий отбор (на ступень выше случайного), производит его на основе полученной информации».

Принято различать системы управления и процессы управления. Рас­смотрение содержания или функций управления относится к процессам управления. Состав функций управления определяется особенностями сис­темы управления и целями исследования.