Постановка многокритериальных задач принятия решений.

Задачи принятия решений, возникающие при управлении системами, как правило, являются многокритериальными, т.к. работа системы обычно описывается несколькими свойствами – локальными критериями.

Пусть f₁ … f_q – критерии по которым оценивается эффективность работы системы. Каждый из q критериев зависит от вектора n параметров. x = {x₁ … x_n} и взаимная важность критериев описывается коэффициентом относительной важности (весами) γ₁ … γ_q.

Критерии f₁ … f_q образует вектор критериев 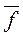, а коэффициент 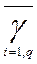- весовой вектор .

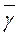Критерии f_i, например, количество и качество вырабатываемой продукции – локальные.

Каждое альтернативное решение u (конкретное значение управляющего воздействия) характеризуется присущей ему векторной оценкой (значением векторного критерия х)

.

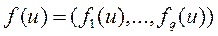Для производственной системы, состоящей из производственных подсистем (агрегаты, установки, цеха, отделы, участки и т.д.) вектор входных параметров x = {x₁ … x_n} может описывать режимные параметры, управляющие воздействием, вектор выходных параметров (в том числе и критерий оценки) – как результаты функционирования систем.

Каждый локальный критерий связан со значениями входных воздействий. Эти зависимости может описывать система моделей объекта.

Задачу принятия решений можно сформулировать следующим образом. Найти вектор управляющих воздействий 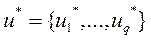, обеспечивающий такие значения локальных критериев, которые удовлетворяют лицо, принимающее решение.

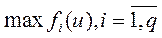
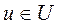
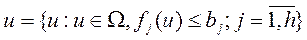
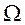- исходное множество управлений