Классификация моделей

Модели классифицируются по временному признаку и по математическому аппарату. По временному признаку математические модели классифицируют на:

1) статические;

2) динамические.

Статические модели предназначены для описания стационарных процессов, т.е. процессов, которые в явном виде не зависят от времени. Условно-статические модели – статические на отрезках времени.

Динамические модели служат для описания нестационарных процессов, т.е. процессов, которые имеют явную зависимость от времени.

Статические модели бывают:

1) аналитические (уравнение зависимости в явном виде);

2) статические статистические (модели дисперсионного, корреляционного, регрессионного анализа);

3) феноменологические (внешний вид регрессионных моделей, однако коэффициенты проставляет сам специалист).

Динамические модели бывают:

1) детерминированные (аналитические);

2) вероятностные (стохастические).

Динамические детерминированные модели имеют вид обыкновенных дифференциальных уравнений первого порядка.

Стохастические модели имеют вид обыкновенных дифференциальных уравнений первого порядка с Винеровской добавкой:

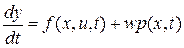
По математическому аппарату математические модели делятся на:

1) детерминированные (аналитические);

2) вероятностные (статистические).

Детерминированные модели могут описываться с помощью аппарата математического анализа конструктивных теорий функций.

Вероятностные модели – могут описываться с помощью теории вероятности, математической статистики и теории случайных процессов.

Статические статистические модели – описывают стационарные процессы методиками регрессионного и дисперсионного анализа, причем регрессионные полиномы имеют вид не более второго порядка.

Статические детерминированные модели – описывают стационарные процессы с помощью теории множеств или аппарата алгебры.

Динамические статистические модели описывают нестационарные процессы с помощью математического аппарата теории случайных процессов и описываются в виде стохастических дифференциальных уравнений.

Динамические детерминированные модели описывают нестационарные процессы в объектах с помощью математического аппарата дифференциальных и интегральных уравнений.

Уравнения в частных производных служат для моделирования в целях исследования объекта. Но для разработки систем оптимального управления объектами такие модели не подходят из-за медленной сходимости метода сеток (метод решения дифференциальных уравнений в частных производных).

При классификации экономико-математических моделей учитыва­ются различные признаки, каждый служит определенной цели. Некоторые типовые группы моделей, которые могут быть положены в основу системы классификации:

• статические и динамические;

• детерминированные и стохастические;

• дискретные и непрерывные;

• линейные и нелинейные;

• балансовые модели;

• имитационные модели;

• модели математического программирования;

• модели, основанные на теории графов;

• модели, основанные на теории вероятностей и математической статистике.

При моделировании сложной системы исследователь обычно иссле­дует совокупность нескольких моделей из числа разновидностей, упомянутых выше. Любая система может быть представлена различными способа­ми, отличающимися по сложности и в деталях. По мере того, как исследо­ватель глубже анализирует и познает проблему, простые модели сменяют­ся все более сложными.