Математическое моделирование

Традиционным представлением о математической модели является ее восприятие как инструмента для прогнозирования последствий альтер­нативных действий с целью выбора наиболее предпочтительного. Однако значительно важнее то, что моделирование — это метод, повышающий эффективность суждений и решений. Математические модели использу­ются для формализации целей, присущих большинству экономических систем, и имеющихся ограничений, налагаемых действующими экономи­ческими законами.

Однако имеется большое количество проблем, не поддающихся аде­кватному моделированию, например: защита окружающей среды от за­грязнений, предотвращение преступности, управление развитием и ростом городов, и т. п., - они характеризуются неясностью и противоречивостью целей, альтернатив развития, диктуемых нестабильными политическими и социальными факторами.

Математические модели многофункциональны, их основные функ­ции характеризуют широту области их применения:

1. модели являются важным средством осмысления действительности (графические, масштабные, сетевые модели);

2. модели выступают своеобразным средством общения, поскольку в сжатой, точной форме позволяют организовать диалог;

3. модели выполняют функцию обучения и тренажа (обучающие программы, имитационные игры на ЭВМ, использующие принципиально отличные от реальных стимулы и мотивы принятия решений);

4. модели широко используются как инструмент прогнозирования и планирования, позволяя рассмотреть значительное число альтернатив и оценить возможные последствия от принятия того или иного решения;

4. моделирование является основным методом оптимизации управленческих решений, отображая или воспроизводя условия развития исследуемого процесса;

5. применение моделей как средства построения экспериментов позволяет осуществлять управление процессом экспериментирования с большей простотой и меньшими затратами, чем если бы эксперимент проводился с реальной системой, получая, зачастую, больше полезной информации о поведении системы в условиях широкого спектра изменяющихся факторов внешней среды.

Экономико-математическая модель — это совокупность матема­тических выражений, описывающих экономические объекты, процессы и явления, исследование которых позволяет получить необходимую инфор­мацию для реализации целей управления, моделируемой системой.

Экономико-математическая модель, как правило, включает три ос­новные составные части:

1)целевую функцию, или функционал модели — математическое выражение цели;

2)систему функциональных ограничений, определяющих пределы изменения исследуемых характеристик объектов, процессов или явлений;

3)систему параметров модели, фиксирующих условия проведения модельного эксперимента (система норм, нормативов, временные параметры реального времени и (или) системного времени, начальные условия и т. п.).

В общем виде статическая экономико-математическая модель сис­темы может быть записана в виде:

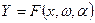(2.7)

где х — экзогенные переменные, или управления, управляемые перемен­ные, факторы, входы;

ω - неуправляемые переменные, или возмущения;

- параметры системы; любые действительные числа;

Y— эндогенные, или зависимые переменные, отклики;

F — определяет вид функциональной зависимости, играет роль оператора преобразования.

Пусть, например, F — линейный оператор. Тогда по определению линейного оператора при х = х₁ + х₂

,

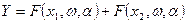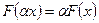
где х₁, х₂- любые функции,

- действительное число.

Линейным оператором является оператор тождественного преобра­зования, дифференцирования, интегрирования, правого сдвига, левого сдвига, суммирования, скалярный оператор.

При изучении экономической системы в движении уравнение модели примет вид:

(2.8)

При этом часто используют две концепции построения динамических моделей: без учета лагов, или запаздываний между входами и выходами — так называемые динамические безынерционные модели; и с учетом лагов — инерционные динамические модели. Безынерционные иначе называют кинематическими. Следует подчеркнуть, что кинематическая модель от­личается от динамической тем, что переходные процессы в системе, обу­словленные ее инерционными и демпфирующими свойствами, не учиты­ваются. В информативном отношении они менее содержательны, чем ди­намические. В английском языке для описания таких систем служат тер­мины «dinamic» и «dinamical».