Лекция № 11. § 11 –1 Метод зон Френеля.
Дифракией называется когерентное рассеяние света на объектах, геометрические размеры которых сранимы с длиной световой волны. Наблюдающаяся дифракционная кар-тина является результатом интерференции вторичных источников, образующихся на по-верхности объекта. Расчет интерференционной картины можно проводить пользуясь мето-дом суперпозиции, однако применение этого метода сопряжено с известными математи-ческими трудностями. В связи мы ограничимся рассмотрения качественного подхода к ре-шению поставленной задачи, развитого Френелем. Основной идеей, определяющей сущ-ность такого рассмотрения, является принцип Гюйгенса –Френеля, который представляет собой дополненный принцип Гюйгенса. Френель постулировал, что все элементарные вто-ричные источники являются когерентнми. Для оценки результирующей амплитуды колебаний в точке наблюдения был разработан специальный метод, получивший название метода зон Френеля. Согласно этому методу волновой фронт (будем называть волновым фронтом поверхность, которая соединяет все точки, колеблющиеся в одинаковой фазе) раз-бивается на отдельные участки, именуемые зонами. Разбиение на зоны должно удовлетво-рять двум условиям:
1.площади всех зон одинаковы,
2.расстояния от двух соседних зон до точки наблюдения отличаются на половину длины волны.
Первое условие означает, что амплитуды колебаний от всех зон в точке наблюдения будут одинаковыми, тогда как из второго условия следует, что колебания двух соседних зон скла-дываются в противофазе. В этом случае вместо вычисления сложных интегралов достаточ-но подсчитать число зон. Если оно – четно – в точке наблюдения будет минимум освещен-ности (зоны попарно гасят друг друга), если же количество зон на участке волнового фрон-та, видимого из точки наблюдения, окажется нечетным – в ней будет конечная освещен-ность.
§ 11 –2 Метод векторных диаграмм.
Для оценки вкладов от каждой зоны в суммарную освещенность используем метод векторных диаграмм. Для этого разобьем каждую зону на ряд узких «подзон» так, что каж-дая подзона отличается от соседней лишь небольшим сдигом по фазе. Колебания каждой из «подзон» будем представлять в виде вектора, длина которого определяется амплитудой ко-
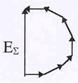 Рис.45. Векторная
диаграмма одной
зоны.
Рис.45. Векторная
диаграмма одной
зоны.
| лебаний. Площади «подзон» выберем одинаковыми. Как видно из рис.45, вектора каждой «подзоны» оказываются повернутыми отно-сительно соседних на небоьшой угол, но «подзоны» на противополож-ных краях зоны отличаются по фазе на 1800 .Суммарное действие всех «подзон» изображается вектором ЕS . Нетрудно сообразить, что при устремлении ширины каждой «подзоны» к нулю, получившаяся лома-ная линия превращается в плавную полуокружность. |
Действие двух зон должно быть равным нулю, но оказывается, что амплитуды колебаний зон не совсем одтнаковые. Их величина зависит от косинуса угла между нормалью к по-верхности зоны и направлением на точку наблюдения. Результат сложения двух и трех зон
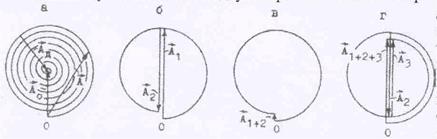 Рис.46. Векторные диаграммы для разного числа зон.
Рис.46. Векторные диаграммы для разного числа зон.
| показан на рис.46( б,в и г). Как видно из рис., две зо-ны почти уничтожаются, а амплитуда третьей зоны почти равна амплитуде первой. Там же показано (рис.46а) действие всего волнового фронта А0, ког-да препятствие отсутству- |
ет. Оно оказывается в два раза меньше, чем действие первой зоны. Витки спирали располо-жены достаточно плотно, и при большом количестве открытыз зон суммарная амплитуда АS » А0 остается практически неизменной при изменении числа зон.
§ 11 –3 Дифракция Френеля на круглом отверстии.
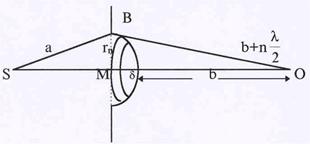 Рис.47. К вычислению радиуса зоны.
Рис.47. К вычислению радиуса зоны.
| Применим метод зон к анализу так называе-мой дифракции Френеля, когда источник света – точечный, и волновая поверхность имеет форму сферы.В качестве препятствия рассмотрим небольшое круглое отверстие в непрозрачном экране. выберем точку наблю-дения О так, чтобы в отверстии укладыва-лось бы целое число зон Френеля. Пусть волновой фронт от точечного источника S, |
дошедший до экрана, имеет радиус SB = а (см. рис.47). Расстояние от точки наблюдения О до плоскости экрана равно МО = b+d. Мысленно разобьем волновой фронт на концентри-ческие зоны ( на рис.47 показана одна зона) так, что расстояние от n – зоны до точки наблю-дения О равно b + nl/2. Из треугольника SBM по теореме Пифагора получим:
МВ2 = SB2 – SM2 = 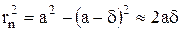 . (IV)
. (IV)
Аналогично из DОМВ : 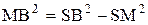 =
= 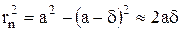 . (V)
. (V)
Члены, содержащие множители l2 и d2, отброшены как малые по сравнению с a и b. При-равнивая правые части уравнений (IV) и (V), получим 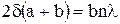 Выражая отсюда d и подставляя его в (IV), получим формулу для радиуса любой зоны:
Выражая отсюда d и подставляя его в (IV), получим формулу для радиуса любой зоны:
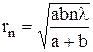 .
.
Численные значения радиуса первой зоны можно оценить, полагая a » b ~ 1м, l » 0,5мкм. Подстановка этих значений показывает, что r1 »0,3 мм. Поэтому при диаметре отверстия 1 - -2 мм в нем уложится 5-7 зон. Поскольку их амплитуды примерно одинаковы, результат сложения существенно зависит от числа зон. При нечетном числе зон в точке наблюдения
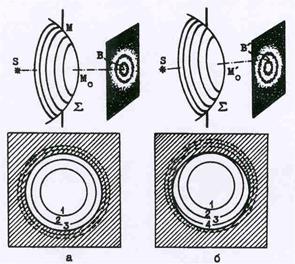 Рис.48. Смещение зон относительно отверстия.
Рис.48. Смещение зон относительно отверстия.
| будет максимум, а при четном – минимум ос-вещенности. Рассмотрим, как будет изменять-ся результат сложения колебаний при измене-нии положения точки О. Если точка смещается вдоль оси SO, то характер разбиения на зоны не изменится, произойдет лишь изменение числа зон, укладывающихся в отверстии, т.е. будет наблюдаться чередование максимумом и минимумов освещенности. Если же точка О смещается перпендикулярно оси SO, то харак- тер разбиения на зоны также не изменится, но произойдет поворот направления наблюдения относительно перпендикуляра, восставленного из центра отверстия к плоскости экрана (см. рис. 48. Вследствие этого часть зон начнет за-крываться, что приведет к изменению осве-щенности. Пусть для определенности в тот мо- |
мент, когда точка наблюдения находится на оси OS, а в отверстии укладывается нечетное число зон (например – три). Когда часть наружной зоны начнет закрываться, освещенность уменьшится.Одновременно с противоположного края отверстия появится часть новой зоны, которая еще больше уменьшит освещенность ( здесь нада вспомнить, что соседние зоны гасят друг друга). Поэтому при дальнейшем удалении точки наблюдения от оси наступит момент, когда освещенность уменьшится до нуля..Это условие будет выполняться для всех точек, находящихся на окружности, радиус которой определяется расстоянием от точки на-блюдения до оси OS. Вокруг светлой точки появится темное кольцо, продолжая рассужде-ния подобным образом, можно придти к заключению, что дифракционная картина от круг-лого отверстия пред-ставляет собой чередование чветлых и темных колец.
§ 11 –4 Дифракция Френеля на круглом экране.
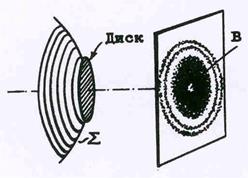 Рис.49. Диффракция на круглом
экране.
Рис.49. Диффракция на круглом
экране.
| Пусть препятствием служит теперь небольшой не-прозрачный диск, и пусть радиус волнового фронта настолько велик, что волновая поверхностьS прак-тически совпадает с плоской поверхностью диска ( рис.49). Разобьем волновой фронт на зоны спосо-бом, аналогичным изложенному в предыдущем па-раграфе. В точку наблюдения В приходят все коле-бания волнового фронта за исключением тех зон, которые закрыты диском. Это суммарное колебание на векторной диаграмме (см. рис.46) изобразится вектором АД . Начало вектора соответствует точке, лежащей на краю диска. При изменении расстоя- |
ния от диска до точки В число закрытых зон будет меняться, и начало вектора АД станет описывать окружность вокруг центра спирали, тогда как конец вектора всегда находится в ее центре. При большом числе открытых зон длина вектора почти не изменяется. Поэтому в точке В будет наблюдаться светлое пятно (пятно Пуассона).
§ 11 –5 Дифракция Фраунгофера.
Этот вид дифракции наблюдается в параллельных лучах, когда волновой фронт ста-новится плоским, а зоны Френеля принимают вид узких прямоугольных полосок. Опти-
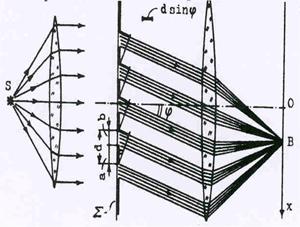 Рис.50. Диффракция Фраунгофера на
щели.
Рис.50. Диффракция Фраунгофера на
щели.
| ческая схема наблюдения этого вида диф-ракции представлена на рис.50. В роли пре-пятствия здесь выступает узкая прямоуголь-ная щель (узкая сторона щели лежит в плос-кости рисунка). Разбиение поверхности щели на зоны Френеля осуществляется следующим образом: через край щели (точка М0 ) прово-дится плоскость (М0 Р), перпендикулярная идущим в точку наблюдения лучам, а затем проводятся параллельные ей плоскости, от-стоящие друг от друга на полволны.Эти плос-кости, пересекая плоскость щели, разбивают ее на зоны Френеля, которые представляют собой полосы, параллельные краям щели: |
границы зон изображаются точками М 0,М1, М2 …, а отрезки М 0М1 , М1М2 определяют ширину первой, второй и т.д.зон.Из рис видно,что в расчете не учитывается разность хода от плоскости М0Р до фокуса линзы Л, предназначенной для создания резкого изображения на экране. Это является следствием таутохронизма линзы, означающего, что лучи прохо-дят пути от М0Р до фокуса линзы за одинаковое время. Попутно заметим, что линза ЛК предназначена для создания параллельного пучка лучей. Предположим, что угол j выбран таким образом, что на ширине щели укладывается целое число зон, т.е. МР = kl/2 ( k = 1,2,3 …). В то же время из DМ0РМ следует, что МР = ММ0 sin j или MP = bsinj. Если число зон четное ( k =2m), то выбранное направление соответствует минимуму освещенности ( зоны попарно гасят друг друга), а если – нечетно (k = 2m-1) – то максимуму. Таким образом, имеем:
bsinj = ml - условие минимума,
bsinj = (2ь-1)l/2 – условие максимума.
При движении точки наблюдения в направлении, перпендикулярном плоскости рисунка (вдоль длинной стороны щели) картина не изменяется, и на экране видны чере-дующиеся темные и светлые полосы. Однако интенсивности светлых полос быстро убы-вают так, что практически с трудом удается наблюдать более двух таких полос с каждой стороны от центрального максимума.
§ 11 –6 Дифракционная решетка.
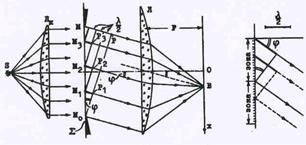 Рис.51. Дифракция на щели.
Рис.51. Дифракция на щели.
| Возьмем теперь в качестве препятствия диф-ракционную решетку, т.е непрозрачную пла-стинку с одинаковыми параллельнымии рав-ноотстоящими друг от друга щелями(рис51). Обозначим, как и прежде, ширину щели b, а ширину непрозрачного участка – а . Величи-ну d = а + b назовем периодом или постоян-ной решетки.Выбирая ту же волновую по-верхность, что и при рассмотрении дифрак- |
ции на одной щели, и применяя принцип Гюйгенса-Френеля, можно заметить, что теперь в каждой точке экрана для наблюдений собираются лучи, идущие от всех N щелей. Для вы-числения результата сложения выделим в каждой щели одинаковые точки(например- верх-ние).Две таких точки в соседних щелях при заданном угле j имеют разность фаз, равную
q = 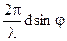 . В точке наблюдения колебания от всех щелей сложатся в одинаковых фазах, если разность фаз q равна 2pn (n =0,1,2…), т.е. q =
. В точке наблюдения колебания от всех щелей сложатся в одинаковых фазах, если разность фаз q равна 2pn (n =0,1,2…), т.е. q = 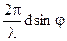 = 2pn, откуда получается ус-ловие для максимумов dsinj = nl . Можно показать, что кроме этих максимумов существу-ют еще другие, положения которых зависит от числа щелей, но интенсивность их крайне не значительна. Чтобы различать эти максимумы с теми, которые удовлетворяют условию dsinj = nl, принято называть их дополнительными максимумами, а максимумы, соответ-ствующие условию dsinj = nl - главными. Значение числа n определяет порядок главного максимума (первый максимум, второй и т.д) Между максимумами должны располагаться минимумы освещенности, но с практической точки зрения они не представляют особого интереса и в нашем курсе не рассматриваются.
= 2pn, откуда получается ус-ловие для максимумов dsinj = nl . Можно показать, что кроме этих максимумов существу-ют еще другие, положения которых зависит от числа щелей, но интенсивность их крайне не значительна. Чтобы различать эти максимумы с теми, которые удовлетворяют условию dsinj = nl, принято называть их дополнительными максимумами, а максимумы, соответ-ствующие условию dsinj = nl - главными. Значение числа n определяет порядок главного максимума (первый максимум, второй и т.д) Между максимумами должны располагаться минимумы освещенности, но с практической точки зрения они не представляют особого интереса и в нашем курсе не рассматриваются.
Полученные условия главных максимумов справедливы для одной длины волны све-та. Если же свет – белый, то для каждого из его составляющих цветов условия максимумов будут соответствовать различным углам j, т.е. на экране получится набор цветных полос. Другими словами, дифракционная решетка позволяет анализировать спектральный состав световых лучей. Поэтому решетку можно использовать как спектральный аппарат. Все спектральные аппараты характеризуются такими величинами как дисперсионная область, угловая дисперсия и разрешающая способность.
Дисперсионная область G определяет ширину спектрального интервала отl доl+ Dl, в котором максимумы для различных волн не перекрываются друг с другом.Величина G =l/n, где n - порядок максимума.
Угловая дисперсия D определяет угловое расстояние между волнами, длина которых отличается на единицу (длины).Выражение для определения D можно получить, дифферен-цируя условия главных максимумов: dcosj =lnd. Отсюда D определяется как
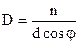 .
.
Под разрешающей способностью А подразумевается возможность спектрального аппарата различать линии, соответствующие близким значениям длин волн l и l + dl. Она определяется выражением
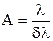 .
.
§ 11 –7 Дифракция рентгеновских лучей.
Рентгеновскими лучами называют электромагнитное излучение, длина волн которого примерно равна !0 –10 м. Длина волны рентгеновских лучей много меньше световых волн,
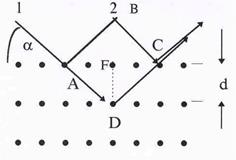 Рис.52. Дифракция рентгенов-
ских лучей.
Рис.52. Дифракция рентгенов-
ских лучей.
| поэтому наблюдать дифракцию этих лучей в стандар-тных схемах не удается. Препятствиями, размеры кото-рых сравнимы с длиной волны рентгеновских лучей, могут служить лишь межатомные расстояния в твер-дых телах. Схема дифракции показана на рис.52. Ато-мы кристалла расположены в правильном порядке, об-разуя плоскости, отражающие лучи. Коэффициент пре-ломления лучей близок к единице, и лучи отражаются от различных плоскостей без заметного преломления (nр » 1). Обозначая угол скольжения лучей через a, а расстояние между отдельными слоями через d, можно |
заметить, что разность хода между интерферирующими лучами d =AD +DC – BC. Из DADF AD = FD/sina; AF = dtga, а из DАВС ВС = 2AFcosa. С учетом того, что AD = DC, имеем:
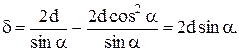
Условие максимума будет выполняться при 2dsina = kl , где k –целое число. Полученная формула носит название формулы Вульфа – Брэггов.
Рассмотренный случай дифракции относится к конкретным межатомным плоскостям и монохроматическому излучению, что заметно упрощает анализ условий образования мак-симумов. В действительности же межатомные плоскости могут быть ориентированы произ- вольным образом, причем в роли интерферирующих лучей могут выступать лучи, отраженные не только от соседних плоскостей. Кроме того, следует иметь ввиду, что реаль-ные кристаллические структуры имют три измерения, каждому из которых могут соответст-вовать различные условия образования максимумов. Тем не менее рентгенографический метод анализа кристаллов нашел широкое применение в петрографии, рентгеноструктур-ном анализе и ряде других приложений.
Поляризация света. Взаимодествие света с веществом.
Дата добавления: 2019-07-26; просмотров: 1324;
