Непосредственные умозаключения
Суждение, содержащее новое знание, может быть получено посредством преобразования некоторого суждения. Так как исходное (преобразуемое) суждение рассматривается как посылка, а суждение, полученное в результате преобразования, — как заключение, умозаключения, построенные посредством преобразования суждений, называютсянепосредственными. К ним относятся:1) превращение, 2) обращение, 3) противопоставление предикату, 4) умозаключения по логическому квадрату.
Выводы в каждом из этих умозаключений получаются в соответствии с логическими правилами, которые обусловлены видом суждения — его количественными и качественными характеристиками.
1. Превращение. Преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения, называется превращением. Превращение опирается на правило:
двойное отрицание равносильно утверждению (┐┐р ≡ р).
Превращать можно общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные суждения.
Общеутвердительное суждение (А) превращается в общеотрицательнов (Е). Например: «Все сотрудники нашего коллектива — квалифицированные специалисты. Следовательно, ни один сотрудник нашего коллектива не является неквалифицированным специалистом».
Схема превращения сужденияА:
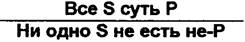
Общеотрицательнов суждение (Е) превращается в общеутвердитвльное (А). Например: «Ни одно религиозное учение не является научным. Следовательно, всякое религиозное учение является ненаучным».
Схема превращения сужденияЕ:
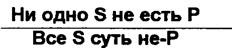
Частноутвердительное суждение (I) превращается в частноотрицательное (О). Например: «Некоторые государства являются федеративными. Следовательно, некоторые государства не являются нефедеративными».
Схема превращения сужденияI:
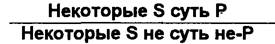
Частноотрицательнов суждение (О) превращается в частноутвердительное (I). Например: «Некоторые преступления не являются умышленными. Следовательно, некоторые преступления являются неумышленными».
Схема превращения сужденияО:
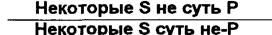
Таким образом, чтобы превратить суждение, нужно заменить его связку на противоположную, а предикат — на понятие, противоречащее предикату исходного суждения. Суждение, полученное посредством превращения, сохраняет количество, но изменяет качество исходного суждения. Субъект исходного суждения не изменяется.
Заключения, полученные посредством превращения, уточняют наши знания. Устанавливая отношения между субъектом и понятием, противоречащим предикату исходного суждения, мы рассматриваем предмет суждения с новой стороны, фиксируя внимание на свойстве, не совместимом со свойством, отраженным в предикате исходного суждения. В этом смысл превращения. Поэтому заключения, полученные с помощью этой логической операции, содержат некоторые новые знания о предмете.
2. Обращение. Преобразование суждения, в результате которого субъект исходного суждения становится предикатом, а предикат — субъектом заключения, называется обращением.
Обращение подчиняется правилу: термин, не распределенный в посылке, не может быть распределен в заключении.
Различают простое (чистое) обращение и обращение с ограничением.
Простым, или чистым называется обращение без изменения количества суждения. Так обращаются суждения, оба термина которых распределены или оба не распределены. Если же предикат исходного суждения не распределен, то он не будет распределен и в заключении, где он становится субъектом. Поэтому его объем ограничивается. Такое обращение называетсяобращением с ограничением.
Общеутвердительное суждение (А) обращается в Частноутвердительное (I), т.е. с ограничением. Например:
«Все студенты нашей группы(S+) сдали экзамены(Р-). Следовательно, некоторые сдавшие экзамены(Р-) — студенты нашей группы(S-)». В исходном суждении предикат не распределен, поэтому он, становясь субъектом заключения, также не может быть распределен. Его объем ограничивается («некоторые сдавшие экзамены»).
Схема обращения сужденияА:

Общеутвердительные выделяющие суждения (в которых предикат распределен) обращаются без ограничения по схеме:
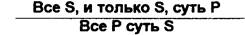
Общеотрицательнов суждение (Е) обращается в общеотрицательное (Е), т.е. без ограничения. Например:
«Ни один студент нашей группы(S+) не является неуспевающим(Р+). Следовательно, ни один неуспевающий(Р+) не является студентом нашей группы(S+)». Простое обращение этого суждения возможно потому, что его предикат («неуспевающие») распределен.
Схема обращения суждения Е:
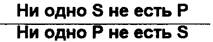
Частноутвердительное суждение (I) обращается в частноутвердительное (I). Это простое (чистое) обращение. Предикат, не распределенный в исходном суждении, не распределен и в заключении. Количество суждения не изменяется. Например: «Некоторые студенты нашей группы (S-) — отличники (Р-). Следовательно, некоторые отличники (Р-) - студенты нашей группы (S-)».
Схема обращения суждения I:

Частноутвердительное выделяющее суждение (предикат распределен) обращается в общеутвердительное. Например:
«Некоторые общественно опасные деяния(S-) являются должностными преступлениями(Р+). Следовательно, все должностные преступления(Р+) являются общественно опасными деяниями(S-)».
Эти суждения обращаются по схеме:
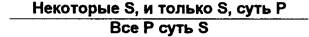
Частноотрицательное суждение (О) не обращается.
Таким образом, обращение суждения не ведет к изменению его качества. Что касается количества, то оно может изменяться (обращение с ограничением), но может оставаться тем же самым (простое, или чистое, обращение).
Умозаключения посредством обращения играют важную роль в процессе рассуждения. Благодаря тому, что предметом нашей мысли становится предмет, отраженный предикатом исходного суждения, мы уточняем наши знания, придаем им большую определенность. Необходимо, однако, строго соблюдать правила ограничения, нарушение которых ведет к ошибкам в рассуждении. Нельзя, например, общеутвердительное суждение, в котором предикат не распределен, обращать без ограничения, нельзя обращать с ограничением Частноутвердительное выделяющее суждение с распределенным предикатом. Так, из суждения «Все студенты юридических вузов изучают логику» следует заключение: «Некоторые изучающие логику — студенты юридических вузов»; из суждения «Некоторые врачи — хирурги» вытекает: «Все хирурги — врачи».
Дата добавления: 2019-07-26; просмотров: 435;
