Противопоставление предикату.

Преобразование суждения, в результате которого субъектом становится понятие, противоречащее пре­дикату, а предикатом — субъект исходного суждения, называется противопоставлением предикату.

Противопоставление предикату может рассматриваться как результат превращения и обращения: превращая ис­ходное суждение S — Р, устанавливаем отношение Sкне-Р;суждение, полученное путем превращения, обращается, в результате устанавливается отношение не-Рк S.

Заключение, полученное посредством противопостав­ления предикату, зависит от количества и качества исходного суждения.

Общеутвердительнов суждение (А) преобразует­ся в общвотрицатвльнов (Е). Например: «Все адвокаты имеют юридическое образование. Следовательно, ни один не имеющий юридического образования не является адвокатом».

Схема противопоставления предикату сужденияА:

Правильность полученного заключения можно прове­рить путем последовательного применения двух логических операций: превращения и обращения. Исходное общеутвер­дительное суждение «Все S суть Р» превращается в общеот­рицательное с отрицательным предикатом «Ни одно S не есть не-Р». Общеотрицательное суждение обращается без ограни­чения. Получаем общеотрицательное суждение «Ни одно не-Р не есть S».

Общеотрицательное суждение (Е) преобразуется в частноутвердительное (I). Например: «Ни одно про­мышленное предприятие нашего города не является убыточ­ным. Следовательно, некоторые неубыточные предприятия являются промышленными предприятиями нашего города».

Схема противопоставления предикату суждения Е:

Проверим правильность заключения с помощью пре­вращения и обращения. Исходное общеотрицательное суж­дение «Ни одно S не есть Р» превращается в общеутверди­тельное с отрицательным предикатом «Все S суть не-Р». Так как предикат общеутвердительного суждения не распределен, его обращение дает частноутвердительное суждение «Некоторые не-Р суть S».

Частноутвердительное суждение (I) посредством противопоставления предикату не преобразуется. Пре­вращение суждения «Некоторые S суть Р» дает частноотрицательное суждение «Некоторые S не суть не-Р». Но частноотрицательное суждение не обращается.

Частноотрицательное суждение (О) преобразу­ется в частноутвердительное (I). Например: «Некоторые свидетели не являются совершеннолетними. Следовательно, некоторые несовершеннолетние являются свидетелями».

Схема противопоставления предикату сужденияО:

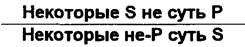
Проверим правильность заключения посредством пре­вращения и обращения. Частноотрицательное суждение «Некоторые S не суть Р» превращается в частноутвердительное «Некоторые S суть не-Р», которое обращается также в част­ноутвердительное«Некоторые не-Р суть S».

Значение умозаключений посредством противопостав­ления предикату состоит в том, что в них выясняется отноше­ние предметов, не входящих в объем предиката, к предметам, отраженным субъектом исходного суждения. Устанавливая отношение между этими предметами, мы уточняем наши зна­ния, высказываем нечто новое, что не было в явной форме выражено в исходном суждении.

4. Умозаключения по логическому квадрату. Учиты­вая свойства отношений между категорическими суждениями А, Е, I, О, которые иллюстрированы схемой логического квад-рата1, можно строить выводы, устанавливая следование ис­тинности или ложности одного суждения из истинности или ложности другого суждения.

Рассмотрим эти выводы.

Отношение противоречия (контрадикторности):

А — О, Е — I.

Поскольку отношения между противоречащими сужде­ниями подчиняются закону исключенного третьего, из истин­ности одного суждения следует ложность другого суждения, из ложности одного — истинность другого. Например, из истин­ности общеутвердительного суждения (А)«Все народы имеют право на самоопределение» следует ложность частноотрицательного суждения (О) «Некоторые народы не имеют права на самоопределение»; из истинности частноутвердительного суждения (I) «Некоторые приговоры суда являются оправда­тельными» следует ложность общеотрицательного суждения (Е) «Ни один приговор суда не является оправдательным».

Выводы строятся по схемам:

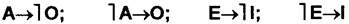
Отношение противоположности (контрарности): А — Е. Из истинности одного суждения следует ложность дру­гого суждения, но из ложности одного из них не следует истинность другого. Например, из истинности общеутверди­тельного суждения (А) «Все народы имеют право на само­определение» следует ложность общеотрицательного сужде­ния (Е)«Ни один народ не имеет права на самоопределение». Но из ложности суждения А «Все приговоры суда являются оправдательными» не следует истинность суждения Е «Ни один приговор суда не является оправдательным». Это суж­дение также ложно.

Отношения между противоположными суждениями подчиняются закону непротиворечия. Выводы строятся по схемам:

Отношение частичной совместимости (субконтрарности): I – O. Из ложности одного суждения следует истин­ность другого, но из истинности одного из них может следо­вать как истинность, так и ложность другого суждения. Истин­ными могут быть оба суждения. Например, из ложного суждения «Некоторые врачи не имеют медицинского образо­вания» следует истинное суждение «Некоторые врачи имеют медицинское образование» (d логическом квадрате слово «некоторые» употребляется в значе­нии «по крайней мере, некоторые»), из истинного суждения «Некото­рые свидетели допрошены» следует суждение «Некоторые свидетели не допрошены», которое может быть как истинным, так и ложным.

Таким образом, субконтрарные суждения не могут быть вместе ложными; по крайней мере одно из них истинно. Выводы строятся по схемам:

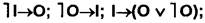
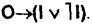
Отношение подчинения (А — I, Е — О). Из истин­ности подчиняющего суждения следует истинность подчинен­ного суждения, но не наоборот: из истинности подчиненного суждения истинность подчиняющего суждения не следует, оно может быть истинным, но может быть ложным. Например, из истинности подчиняющего суждения А «Все врачи имеют ме­дицинское образование» следует истинность подчиненного ему суждения I «Некоторые врачи имеют медицинское обра­зование». Из истинного подчиненного суждения «Некоторые свидетели допрошены» нельзя с необходимостью утверждать об истинности подчиняющего суждения «Все свидетели до­прошены».

Выводы строятся по схемам:

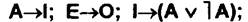
Из ложности подчиненного суждения следует ложность подчиняющего суждения, но не наоборот: из ложности подчи­няющего суждения ложность подчиненного с необходимостью не следует, оно может быть истинным, но может быть и лож­ным. Например, из ложности подчиненного суждения (О) «Некоторые народы не имеют права на самоопределение» следует ложность подчиняющего суждения (Е) «Ни один на­род не имеет права на самоопределение». Если ложным яв­ляется подчиняющее суждение (А) «Все свидетели допрошены», то подчиненное ему суждение (I) «Некоторые свидетели допрошены» может быть истинным, но может быть ложным (возможно, что ни один свидетель не допрошен).

Выводы строятся по схемам:

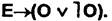
Знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.

Умозаключения по логическому квадрату находят при­менение во многих мыслительных приемах и операциях, в том числе в аргументации, где построение некоторых способов косвенного доказательства и косвенного опровержения опи­раются на отношения противоречия.