Метод искусственных переменных (М-метод)
В рассматриваемой вычислительной схеме симплекс-метода для получения начального базисного решения используются дополнительные переменные. Допустимое базисное решение получается в случае, когда ограничения вида « 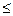 ». Однако для ограничений вида «
». Однако для ограничений вида « 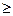 » или «=» начальное базисное решение может быть недопустимым.
» или «=» начальное базисное решение может быть недопустимым.
Для получения системы в каноническом виде, обладающей допустимым базисным решением, существует специальный метод. Сначала задача ЛП приводится к канонической форме, в которой все переменные неотрицательные. Затем для каждого ограничения проверяется существование соответствующей базисной переменной. Если ее нет, то вводится новая искусственная переменная 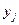 с тем же знаком, что и свободный член (искусственных переменных столько, сколько ограничений дающих отрицательную компоненту в первоначальном базисе), играющая роль базисной для данного ограничения. После проверки всех ограничений получается расширенная система в каноническом виде и появляется возможность заполнить начальную симплексную таблицу. Так как введенные переменные не имеют отношения к существу задачи ЛП в исходной постановке, то необходимо добиться обращения в нуль искусственных переменных. для этого составляем новую целевую функцию
с тем же знаком, что и свободный член (искусственных переменных столько, сколько ограничений дающих отрицательную компоненту в первоначальном базисе), играющая роль базисной для данного ограничения. После проверки всех ограничений получается расширенная система в каноническом виде и появляется возможность заполнить начальную симплексную таблицу. Так как введенные переменные не имеют отношения к существу задачи ЛП в исходной постановке, то необходимо добиться обращения в нуль искусственных переменных. для этого составляем новую целевую функцию 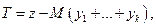 где
где 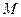 - произвольное, большое по отношению задаче число; k - количество искусственных переменных, и ищем максимальное значение Т-функции.
- произвольное, большое по отношению задаче число; k - количество искусственных переменных, и ищем максимальное значение Т-функции.
Справедливы следующие утверждения.
1). Если в оптимальном решение Т-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи.
2). Если имеется оптимальное решение Т-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи несовместна.
3). Если максимум Т-функции равен бесконечности, то исходная задача неразрешима (либо система несовместна, либо максимум неограничен).
На практике, как правило, Т -задачу разбивают на две задачи и решают с помощью двухэтапного симплек-метода.
Этап 1. Рассматривается искусственная целевая функция 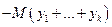 которая максимизируется при помощи симплекс-метода. Другими словами, производится исключение искусственных переменных. Если максимальное значение вспомогательной задачи равно нулю, то все искусственные переменные обращаются в нуль, и получается допустимое базисное решение начальной задачи. Далее реализуется этап 2. Если максимальное значение вспомогательной задачи положительное, то, по крайней мере, одна из искусственных переменных также положительная, что свидетельствует о противоречивости начальной задачи, и вычисления прекращаются.
которая максимизируется при помощи симплекс-метода. Другими словами, производится исключение искусственных переменных. Если максимальное значение вспомогательной задачи равно нулю, то все искусственные переменные обращаются в нуль, и получается допустимое базисное решение начальной задачи. Далее реализуется этап 2. Если максимальное значение вспомогательной задачи положительное, то, по крайней мере, одна из искусственных переменных также положительная, что свидетельствует о противоречивости начальной задачи, и вычисления прекращаются.
Этап 2. Допустимое базисное решение, найденное на первом этапе, улучшается в соответствии с целевой функцией исходной задачи ЛП на основе симплекс-метода, т.е. оптимальная таблица первого этапа превращается в начальную таблицу второго этапа и изменяется целевая функция.
Пример.
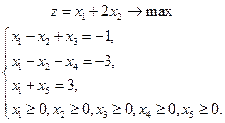
Вектор 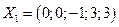 не образует начального допустимого решение (начальное допустимое решение получается приравниванием нулю основных переменных в каноническое системе ограничений). В первое ограничение, дающее отрицательную компоненту, введем искусственную переменную
не образует начального допустимого решение (начальное допустимое решение получается приравниванием нулю основных переменных в каноническое системе ограничений). В первое ограничение, дающее отрицательную компоненту, введем искусственную переменную 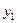 .
.
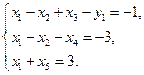
Преобразуем систему ограничений, умножив первое и второе уравнение на 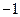 .
.
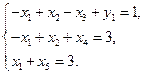
Т -функция имеет вид: 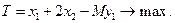 Заполняем первую симплекс-таблицу:
Заполняем первую симплекс-таблицу:
| Базис | Свободный | Переменные | Оценочные | |||||
| член | отношения | |||||||
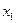
| 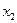
| 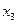
| 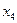
| 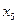
| 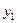
| |||
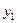
| -1 | -1 | ||||||
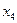
| -1 | |||||||
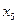
| 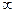
| |||||||
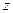
| -1 | -2 | ||||||
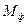
| -М | М | -М | М | -M |
Последняя строка таблицы -это (-М-функция), т.е. 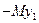 . Заполняется она путем выражения искусственных переменных через небазисные переменные (Строки, в которых присутствует искусственная переменная умножаются на
. Заполняется она путем выражения искусственных переменных через небазисные переменные (Строки, в которых присутствует искусственная переменная умножаются на 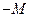 и соответствующие их компоненты складываются; в данном случае умножается первая строка. В качестве оценочной строки рассматривается строка
и соответствующие их компоненты складываются; в данном случае умножается первая строка. В качестве оценочной строки рассматривается строка 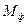 , Критерий оптимальности не выполнен. Отрицательный коэффициент соответствует столбцу
, Критерий оптимальности не выполнен. Отрицательный коэффициент соответствует столбцу 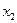 . Считаем оценочные отношения и находим переменную, выводимую из базиса -
. Считаем оценочные отношения и находим переменную, выводимую из базиса - 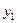 .Переходим к новой симплекс-таблице.
.Переходим к новой симплекс-таблице.
| Базис | Свободный | Переменные | Оценочные | |||||
| член | отношения | |||||||
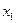
| 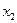
| 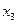
| 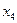
| 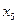
| 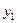
| |||
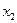
| -1 | -1 | ||||||
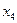
| ||||||||
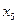
| ||||||||
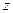
| -3 | -2 | -2 | |||||
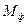
|
Последняя строка показывает, что критерий оптимальности выполнен: 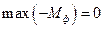 . Искусственная переменная тоже равна нулю. Допустимое базисное решение получено
. Искусственная переменная тоже равна нулю. Допустимое базисное решение получено 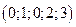 . Далее, отбросив последнюю строку и столбец с искусственной переменной переходим ко второму этапу.
. Далее, отбросив последнюю строку и столбец с искусственной переменной переходим ко второму этапу.
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
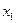
| 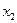
| 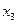
| 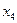
| 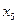
| |||
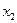
| -1 | -1 | |||||
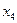
| |||||||
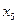
| |||||||
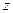
| -3 | -2 |
Дата добавления: 2019-07-26; просмотров: 1441;
