Функции для расчета финансовых потоков

Текущая стоимость потока PV растет и со временем достигает уровня будущей стоимости FV. Как правило, разница между стоимостями этих потоков выражается не в абсолютных единицах (R = FV – PV), а в относительных единицах r = PV/FV (рис. 10.32).

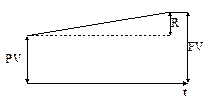
Рис. 10.32. Соотношение стоимостей потоков

1. Текущая стоимость инвестиций PV по ставке, числу периодов выплат, периодическим выплатам и/или выплатам в конце периода (стоимость денег, даваемых или взятых в долг, на текущий момент; сколько деньги стоят сейчас).

1.1. Периодические выплаты отсутствуют или одинаковы: ПС (Приведенная Стоимость) (ПЗ).

Задача. Какая начальная сумма необходима для получения ежегодных выплат в размере 1 000 руб в течении 4 лет, если процентная ставка равна 10% годовых?

Решение. Определим для каждой ежегодно выплачиваемой 1 000 тот начальный доход, который она даст:

PV = 1 000/l,10 + 1 000/(l,10)² + 1 000/(l,10)³ + 1 000/(l,10)⁴ = 3 169,87.

Формат функции: ПС(r; n; плт; [FV]; [тип]),

где плт – размер периодической выплаты; тип – 0, если выплата производится в конце периода, и 1, если в начале.

Формула для решения задачи:

=ПС(0,1; 4; 1000) (Результат: 3 169,87).

1.2. Выплаты могут быть различными, но их периодичность сохраняется: ЧПС (Чистая Приведенная Стоимость) (НПЗ).

1.3. Выплаты и их периодичность могут быть различными: ЧИСТНЗ.

2. Будущая стоимость инвестиций FV по ставке, числу периодов выплат, периодическим выплатам, текущей стоимости (отдача от текущей стоимости денег; сколько деньги будут стоить).

2.1. Периодические выплаты и ставка постоянны: БС (Будущая Стоимость) (БЗ).

Задача. Определить будущую величину вклада в 10 000 руб, помещенного в банк на 3 года под 5% годовых, если начисление процентов осуществляется:

а) раз в году; б) раз в месяц.

Решение. Формат функции: БС(r; n; плт; PV; [тип]).

Формулы для решения задачи:

а) =БС(0,05; 3; 0; -10000) (Результат: 11 576,25);

б) =БС(0,05/12; 3*12; 0; -10000) (Результат: 11 614,72).

Ставка обычно задается в виде десятичной дроби: 5% – 0,05; 10% – 0,1; 100% – 1 и т. д.

Если начисление процентов осуществляется m раз в году, аргументы r и n необходимо скорректировать следующим образом:

r = r / m;

n = n ´ m.

Аргумент PV здесь задан в виде отрицательной величины (-10 000), так как с точки зрения вкладчика эта операция влечет за собой отток его денежных средств в текущем периоде с целью получения положительной величины (11 576,25) через 3 года.

Однако для банка, определяющего будущую сумму возврата средств по данному депозиту, этот аргумент должен быть задан в виде положительной величины, так как означает поступление средств (увеличение пассивов):

=БС(0,05; 3; 0; 10000) (Результат: -11 576,25).

Полученный же при этом результат – отрицательная величина, так как операция означает расходование средств (возврат банком денег вкладчику).

Последний аргумент функции тип опущен, так как начисление процентов в подобных операциях, как правило, осуществляется в конце каждого периода. В противном случае функция была бы задана с указанием всех аргументов.

2.2. Периодические выплаты отсутствуют, ставка в разные периоды различна: БЗРАСПИС.

3. Определение ставки (скорости оборота средств, ставки доходности) r по числу периодов, текущей и будущей стоимостям инвестиций.

3.1. Единовременные и периодические выплаты отсутствуют или постоянны: СТАВКА (НОРМА).

Задача. Вложение в 10 000 руб гарантирует 15 000 руб через 3 года. Определить скорость оборота средств.

Решение. Формат функции:

СТАВКА(n;плт;PV;[FV][;тип][;предположение]),

где предположение – предполагаемая величина ставки.

Формула для решения задачи:

=СТАВКА(3;;-10000;15000) (Результат 14%).

Значение PV – отрицательное, так как средства изымаются у вкладчика, а FV – положительное, так как средства возвращаются.

3.2. Выплаты могут быть различными, но их периодичность сохраняется: ВСД (Внутренняя Ставка Доходности) (ВНДОХ).

3.3. Выплаты могут быть различными, но их периодичность сохраняется, при этом деньги получены под одну ставку, затем инвестируются под другую ставку: МВСД (Модифицированная Внутренняя Ставка Доходности).

3.4. Выплаты и их периодичность могут быть различными: ЧИСТВНДОХ (Чистый Внутренний Доход).