Законы распределения
Значение биномиального распределения (распределения Бернулли, формулы Бернулли):
БИНОМРАСП(k; n; p; признак),
где k – количество успешных испытаний; n – число независимых испытаний; p – вероятность успеха в каждом испытании; признак – логическое значение, определяющее форму функции.
Если параметр признак имеет значение ИСТИНА, то функция возвращает интегральную функцию распределения, то есть вероятность того, что число успешных испытаний не более значения параметра k. Если этот параметр имеет значение ЛОЖЬ, то возвращается функция распределения, то есть вероятность того, что число успешных испытаний в точности равно значению параметра k.
Параметры k и n усекаются до целых.
Функция возвращает значение ошибки #ЗНАЧ!, если k, n или p не является числом.
Функция возвращает значение ошибки #ЧИСЛО! в следующих случаях:
1) k < 0 или k > n;
2) p < 0 или p > 1.
Формула расчета значения интегрального биномиального распределения:
Pn(x ≤ k) = 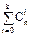 pi(1 – p)n–i.
pi(1 – p)n–i.
Формула расчета значения биномиального распределения:
Pn(x = k) = 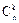 pk(1 – p)n–k.
pk(1 – p)n–k.
Значение гипергеометрического распределения:
ГИПЕРГЕОМЕТ(m; n; M; N),
где m – число успехов в выборке; n – размер выборки; M – число успехов в генеральной совокупности; N – размер генеральной совокупности.
Все аргументы усекаются до целых.
Если любой из аргументов не является числом, то функция возвращает значение ошибки #ЗНАЧ!.
Функция возвращает значение ошибки #ЧИСЛО! в следующих случаях:
1) m < 0 или m > min{n, M};
2) m < min{0; n – N + M};
3) n < 0 или n > N;
4) M < 0 или M > N;
5) N < 0.
Формула расчета значения гипергеометрического распределения:
P = 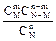 .
.
Значение функции нормального распределения для указанного среднего и стандартного отклонения:
НОРМРАСП(x; a; s; признак),
где x – значение, для которого строится распределение; a – математическое ожидание нормального распределения; s – среднее квадратическое отклонение; признак – логическое значение, определяющее форму функции.
Если параметр признак имеет значение ИСТИНА, то функция возвращает интегральную функцию распределения. Если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.
Функция возвращает значение ошибки #ЗНАЧ!, если a или s не является числом.
Функция возвращает значение ошибки #ЧИСЛО!, если s ≤ 0.
Формула интегральной функции нормального распределения:
F(x) = 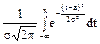 .
.
Формула плотности нормального распределения:
f(x) = 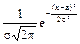 ,
,
Если a = 0, s = 1 и признак = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, то есть НОРМСТРАСП:
НОРМСТРАСП(x),
где x – значение, для которого строится распределение.
Формула плотности стандартного нормального распределения:
j(x) = 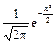 .
.
Значение распределения Пуассона:
ПУАССОН(k; l; признак),
где k – количество событий; l – среднее количество событий в единицу времени; признак – логическое значение, определяющее форму возвращаемого распределения вероятностей.
Если параметр признак имеет значение ИСТИНА, то функция возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий будет от 0 до k включительно. Если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения Пуассона, то есть вероятность того, что число событий равно k.
Параметр k усекается до целого.
Функция возвращает значение ошибки #ЗНАЧ!, если k или l не является числом.
Функция возвращает значение ошибки #ЧИСЛО! в следующих случаях:
1) k ≤ 0;
2) l ≤ 0.
Формула расчета интегрального распределения Пуассона:
Pn(x £ k) = 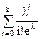 .
.
Функция плотности распределения Пуассона:
Pn(x = k) = 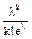 .
.
Дата добавления: 2019-04-03; просмотров: 366;
